Радиальная основная функция имеет форму
то, где x является n-мерным вектором,
является n-мерным вектором, названным центром радиальной основной функции, ||. || обозначает Евклидово расстояние и одномерная функция, заданная для положительных входных значений, которые мы назовем функцией профиля.
Модель создается как линейная комбинация радиальных основных функций N с отличными центрами N. Учитывая входной вектор x, вывод сети RBF является вектором действия
, данным
то, где
вес сопоставлен с jth радиальной основной функцией, центрировалось в
, и
. Вывод
аппроксимирует целевое множество значений, обозначенное y.
Множество радиальных основных функций доступно в MBC, каждый охарактеризованный формой
. Все радиальные основные функции также имеют связанный параметр ширины
, который связан с распространением функции вокруг ее центра. Выбор поля в образцовой настройке обеспечивает настройку по умолчанию для ширины. Ширина по умолчанию является средним значением по центрам расстояния каждого центра его самому близкому соседу. Это - эвристика, данная в Hassoun (см. Ссылки) для Gaussians, но это - только грубое руководство, которое обеспечивает отправную точку для алгоритма выбора ширины.
Другой параметр, сопоставленный с радиальными основными функциями, является параметром регуляризации
. Это (обычно маленький) положительный параметр используется в большинстве алгоритмов подбора. Параметр
штрафует большие веса, который имеет тенденцию производить более сглаженные приближения y и уменьшать тенденцию сети сверхсоответствовать (то есть, соответствовать целевым значениям y хорошо, но иметь плохую прогнозирующую возможность).
Следующие разделы объясняют различные параметры для радиальных основных функций, доступных в продукте Model-Based Calibration Toolbox™, и как использовать их для моделирования.
В диалоговом окне Model Setup можно выбрать который ядро RBF использовать. Ядра являются типами RBF (мультиквадрика, Гауссова, thinplate, и так далее). Эти типы описаны в следующих разделах.
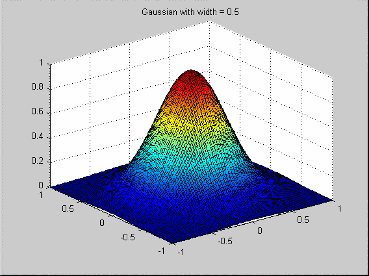
Это - радиальная основная функция, обычно используемая в сообществе нейронной сети. Его функция профиля
Это приводит к радиальной основной функции
В этом случае параметр ширины совпадает со стандартным отклонением Гауссовой функции.
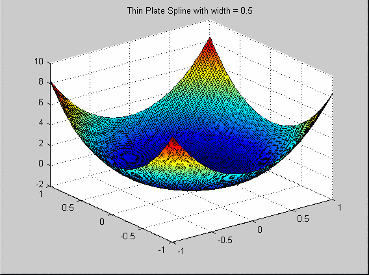
Эта радиальная основная функция является примером сплайна сглаживания, как популяризировано Грэйс Уохбой (http://www.stat.wisc.edu/~wahba/). Они обычно добавляются полиномиальными условиями младшего разряда. Его функция профиля
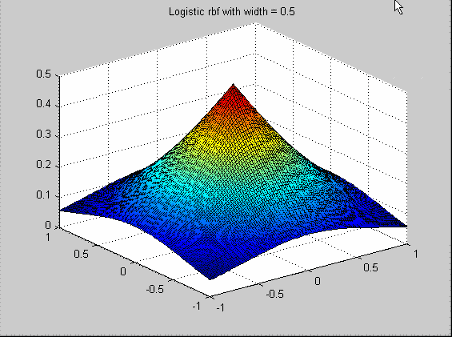
Эти радиальные основные функции упоминаются в Hassoun (см. Ссылки). У них есть функция профиля
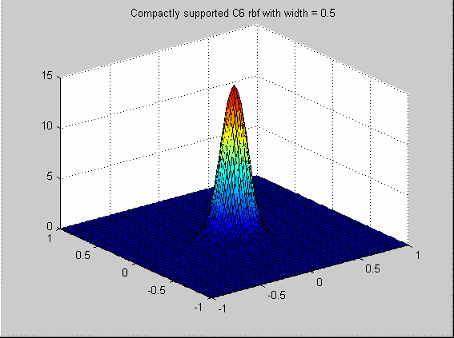
Они формируют семейство радиальных основных функций, которые имеют функцию профиля кусочного полинома и компактную поддержку [Wendland, видят Ссылки]. Член семейства, чтобы выбрать зависит от размерности пробела (n), от которого данные чертятся и желаемая сумма непрерывности полиномов.
| Размерность | Непрерывность | Профиль |
|---|---|---|
n=1 | 0 |
|
2 |
| |
4 |
| |
n=3 | 0 |
|
2 | ||
4 |
| |
n=5 | 0 |
|
2 |
| |
4 |
|
Мы использовали обозначение
для положительной части a.
Когда n даже, радиальная основная функция, соответствующая размерности n+1, используется.
Обратите внимание на то, что каждая из радиальных основных функций является ненулевой, когда r находится в [0,1]. Возможно изменить поддержку, чтобы быть
заменой r
в предыдущей формуле. Параметр
все еще упоминается как ширина радиальной основной функции.
Подобные формулы для функций профиля существуют для n> 5, и для даже непрерывности> 4. Функции Вендлэнда доступны до ровной непрерывности 6, и в любой размерности пробела n.
Примечания по использованию
Лучшие свойства приближения обычно сопоставляются с более высокой непрерывностью.
Поскольку определенные данные установили параметр ширины для функций Вендлэнда, должно быть больше, чем ширина, выбранная для Гауссова.
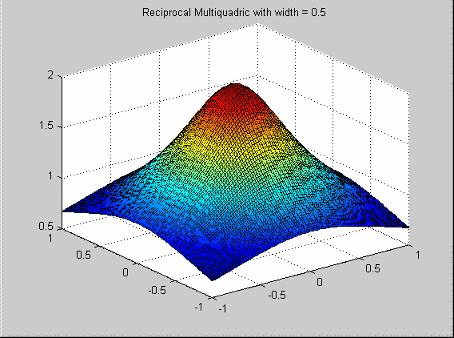
Это популярный инструмент для подбора кривой данных, имеющий разброс. У них есть функция профиля
.
Они имеют функцию профиля
Обратите внимание на то, что ширина
нуля недопустима.
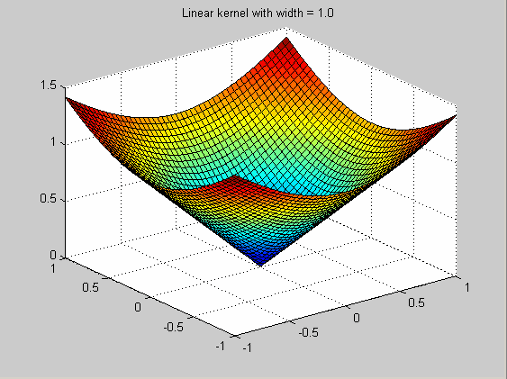
Они имеют функцию профиля
.
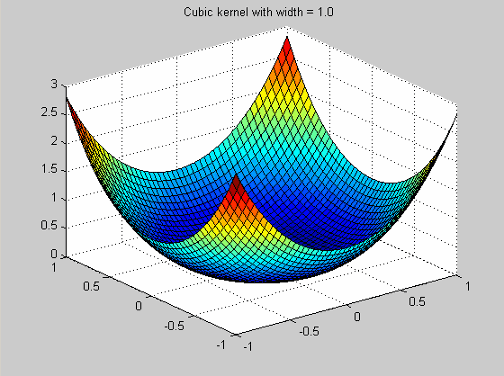
Они имеют функцию профиля
.
Существует четыре характеристики RBF, который должен быть решен: веса, центры, ширина, и
. Каждый из них может оказать значительное влияние на качество получившейся подгонки, и должны быть определены хорошие значения для каждого из них. Веса всегда определяются путем определения центров, ширины, и
, и затем решения соответствующей линейной системы уравнений. Однако проблема определения хороших центров, ширины, и
во-первых совсем не проста, и осложнена сильными зависимостями среди параметров. Например, оптимальное
значительно отличается, когда параметр ширины изменяется. Глобальный поиск по всем возможным центральным местоположениям, ширине, и
в вычислительном отношении препятствует во всех кроме самой простой из ситуаций.
Чтобы попытаться сражаться с этой проблемой, подходящие стандартные программы существуют трех разных уровней.
На самом низком уровне алгоритмы, которые выбирают соответствующие центры данных значений ширины и
. Центры выбраны по одному из набора кандидата (обычно набор точек данных или подмножество их). Получившиеся центры поэтому оцениваются в грубом порядке важности.
В среднем уровне алгоритмы, которые выбирают соответствующие значения для
и центры, учитывая заданную ширину.
В верхнем уровне алгоритмы, которые стремятся находить хорошие значения для каждого из центров, ширины, и
. Эти алгоритмы верхнего уровня тестируют различные значения ширины. Для каждого значения ширины один из алгоритмов среднего уровня называется, который определяет хорошие центры и значения для
.
Эти алгоритмы и их подходящие параметры описаны в следующих разделах:
Это - основной алгоритм, как описано в Чене, Chng, и Alkadhimi [Видят Ссылки]. В Rols (Упорядоченные Ортогональные Наименьшие квадраты) центры выбраны по одному из набора кандидата, состоящего из всех точек данных или подмножества этого. Это выбирает новые центры в прямой процедуре отбора. При запуске с нулевых центров на каждом шаге выбран центр, который уменьшает упорядоченную ошибку большинство. На каждом шаге матрица X регрессии анализируется с помощью Алгоритма Грама-Шмидта в продукт X = WB, где W имеет ортогональные столбцы, и B верхний треугольный с единицами на диагонали. Это подобно по своей природе разложению QR. Упорядоченная ошибка дана тем
, где g = Bw и e является невязкой, данной
. Минимизация упорядоченной ошибки совершает
небольшую ошибку квадрата суммы, в то время как одновременно не разрешение
становится слишком большим. Когда g связан с весами g = Bw, это имеет эффект держания под контролем весов и сокращения сверхподгонки. Термин
, а не сумма квадратов весов
используется, чтобы повысить эффективность.
Алгоритм останавливается или когда максимальное количество центров достигнуто, или добавление, что новые центры значительно не уменьшают упорядоченное ошибочное отношение (управляемый пользовательским допуском).
Подходящие Параметры. Maximum number of centers — максимальное количество центров, которые может выбрать алгоритм. Значением по умолчанию являются меньшие из 25 центров или π количества точек данных. Форматом является min(nObs/4, 25). Можно ввести значение (например, введение 10 производит десять центров), или отредактируйте существующую формулу (например, (nObs/2, 25) производит половину количества точек данных или 25, какой бы ни меньше).
Percentage of data to be candidate centers — Процент точек данных, которые должны использоваться в качестве центров кандидата. Это определяет подмножество точек данных, которые формируют пул, чтобы выбрать центры из. Значение по умолчанию составляет 100%, то есть, чтобы рассмотреть все точки данных как возможные новые центры. Это может уменьшаться, чтобы ускорить время выполнения.
Regularized error tolerance — Средства управления, сколько центров выбрано перед алгоритмом, останавливаются. Смотрите Чена, Chng и Alkadhimi [Ссылки] для деталей. Этот параметр должен быть положительным числом между 0 и 1. Большие допуски означают, что выбрано меньше центров. Значение по умолчанию 0.0001. Если меньше, чем максимальное количество центров выбираются, и вы хотите обеспечить выбор максимального количества, затем уменьшать допуск до эпсилона (eps).
RedErr обозначает Уменьшаемую Ошибку. Этот алгоритм также начинает с нулевых центров и выбирает центры в прямой процедуре отбора. Алгоритм находит (среди точек данных еще не выбранный) точку данных с самой большой невязкой и выбирает ту точку данных в качестве следующего центра. Этот процесс повторяется, пока максимальное количество центров не достигнуто.
Подходящие Параметры. Только имеет Number of centers.
Этот алгоритм основан на эвристике, что необходимо поместить больше центров в область, где существует больше изменения в невязке. Для каждой точки данных группа соседей идентифицирована как точки данных на расстоянии sqrt (nf) разделенный на максимальное количество центров, где nf является рядом факторов. Средние невязки в группе соседей вычисляются, затем объем покачивания невязки в области той точки данных задан, чтобы быть суммой квадратов различий между невязкой в каждом соседе и средними невязками соседей. Точка данных с большей частью покачивания выбрана, чтобы быть следующим центром.
Подходящие Параметры. Почти как в алгоритме Rols, ни кроме какого Regularized error.
Этот алгоритм берет концепцию из оптимального Проекта Экспериментов и применяет его к центральной проблеме выбора в радиальных основных функциях. Набор кандидата центров сгенерирован латинским гиперкубом, метод, который обеспечивает квазиравномерное распределение точек. От этого набора кандидата, n центры выбраны наугад. Этот набор увеличивается p новыми центрами, затем этот набор центров n+p уменьшается до n путем итеративного удаления центра, который приводит к лучшей статистической величине НАЖАТИЯ (как в пошаговом). Этот процесс повторяется число раз, заданное в Number of augment/reduce cycles.
CentreExchange и Tree Regression (см. Древовидную Регрессию) являются единственными алгоритмами, которые разрешают центрам, которые не расположены в точках данных. Это означает, что вы не видите центры на образцовых графиках. Алгоритм CentreExchange имеет потенциал, чтобы быть более гибким, чем другие центральные алгоритмы выбора, которые выбирают центры, чтобы быть подмножеством точек данных; однако, это является значительно более трудоемким и не рекомендуемое на больших проблемах.
Подходящие Параметры. Number of centers — количество центров, которые будут выбраны
Number of augment/reduce cycles — Число раз, что центральный набор увеличивается, затем уменьшало
Number of centers to augment by — Каким количеством центров, чтобы увеличиться
Lambda является параметром регуляризации.
Для заданной ширины этот алгоритм оптимизирует параметр регуляризации относительно критерия GCV (обобщенная перекрестная проверка; смотрите обсуждение под критерием GCV).
Начальная буква центрируется или выбрана одним из низкоуровневых центральных алгоритмов выбора или предыдущим выбором центров, используется (см. обсуждение под параметром Do not reselect centers). Можно выбрать начальное значение запуска для
путем тестирования начального количества значений для lambda (установленный пользователем), которые равномерно распределены на логарифмическом масштабе между 10-10 и 10 и выбор того с лучшим счетом GCV. Это помогает постараться не попадать в локальные минимумы на GCV -
кривая. Параметр
затем выполнен с помощью итераций, чтобы попытаться минимизировать GCV использование формул, данных в разделе критерия GCV. Итерация останавливается, когда или максимальное количество обновлений достигнуто или log10 (GCV) изменения значения меньше, чем допуск.
Подходящие Параметры. Center selection algorithm — центральный алгоритм выбора для использования.
Maximum number of updates — Максимальное количество времен, которыми
сделано обновление. Значение по умолчанию равняется 10.
Minimum change in log10(GCV) — Допуск. Это задает останавливающийся критерий итерации
; обновление останавливается, когда различием в log10 (GCV) значение являются меньше, чем допуск. Значение по умолчанию 0.005.
Number of initial test values for lambda — Количество тестовых значений
определить начальное значение для
. Установка этого параметра на 0 средних значений, что лучшее
до сих пор используется.
Do not reselect centers for new width — Этот флажок определяет, повторно выбраны ли центры для нового значения ширины, и после каждого обновления lambda, или если лучшие центры до настоящего времени должны использоваться. Более дешево сохранить лучшие центры найденными до сих пор, и часто это достаточно, но это может вызвать преждевременную сходимость к определенному набору центров.
Отображение Когда вы устанавливаете этот флажок, этот алгоритм строит результаты алгоритма. Отправная точка для
отмечена черным кругом. Как
обновляется, новые значения построены как красные кресты, соединенные с красными линиями.
Найденное лучшее отмечено зеленой звездочкой.
Если слишком много графиков, вероятно, будут произведены из-за флажка Display, активируемого здесь, предупреждение сгенерировано, и у вас есть опция, чтобы остановить выполнение.
Нижняя граница 10-12 помещается в
, и верхняя граница 10.
Для заданной ширины этот алгоритм оптимизирует параметр регуляризации в алгоритме Rols относительно критерия GCV. Начальная подгонка и центры выбраны Rols с помощью предоставленного пользователями
. Как в IterateRidge, вы выбираете начальное значение запуска для
путем тестирования начального количества значений запуска для lambda, которые равномерно распределены на логарифмическом масштабе между 10-10 и 10, и выбор того с лучшим счетом GCV.
затем выполнен с помощью итераций, чтобы улучшить GCV. Каждый раз, который
обновляется, центральный процесс выбора, повторяется. Это означает, что IterateRols является намного более в вычислительном отношении дорогим, чем IterateRidge.
Нижняя граница 10-12 помещается в
, и верхняя граница 10.
Подходящие Параметры. Center selection algorithm — центральный алгоритм выбора для использования. Для IterateRols единственным центральным доступным алгоритмом выбора является Rols.
Maximum number of updates — То же самое что касается IterateRidge.
Minimum change in log10(GCV) — То же самое что касается IterateRidge.
Number of initial test values for lambda — То же самое что касается IterateRidge.
Do not reselect centers for new width — Этот флажок определяет, повторно выбраны ли центры для нового значения ширины или если лучшие центры до настоящего времени должны использоваться.
Отображение Когда вы устанавливаете этот флажок, этот алгоритм строит результаты алгоритма. Отправная точка для
отмечена черным кругом.
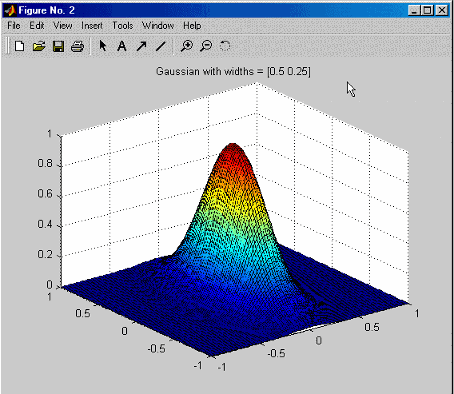
Когда вышеупомянутая фигура обновляется, новые значения построены как красные кресты, соединенные с красными линиями.
Найденное лучшее отмечено зеленой звездочкой.
Если слишком много графиков, вероятно, будут произведены из-за флажка Display, активируемого здесь, предупреждение сгенерировано, и у вас есть опция, чтобы остановить выполнение.
Этот алгоритм комбинирует центральный выбор и процессы выбора lambda. Вместо того, чтобы ожидать, пока все центры не выбраны прежде
, обновляется (как с другими алгоритмами выбора lambda), этот алгоритм предлагает способность обновить
после того, как каждый центр выбран. Это - прямой алгоритм выбора, который, как Rols, выбирает центры на основе упорядоченного ошибочного сокращения. Останавливающийся критерий StepItRols является на основе log10 (GCV) изменением меньше, чем допуск больше, чем конкретное количество раз подряд (данный в параметре Maximum number of times log10(GCV) change is minimal). Если сложение центров остановилось, промежуточная подгонка с самым маленьким log10 (GCV) выбрана. Это может включить удаление некоторых центров, которые вошли поздно в алгоритм.
Подходящие Параметры. Maximum number of centers — Как в алгоритме Rols.
Percentage of data to candidate centers — Как в алгоритме Rols.
Number of centers to add before updating — Сколько центров выбрано, прежде чем итерация
начинается.
Minimum change in log10(GCV) — Допуск. Это должно быть положительное число между 0 и 1. Значение по умолчанию 0.005.
Maximum number of times log10(GCV) change is minimal — Средства управления, сколько центров выбрано перед алгоритмом, останавливаются. Значение по умолчанию равняется 5. Оставленный в значении по умолчанию, центральный выбор останавливается, когда log10 (GCV) значения изменяются меньше, чем допуск пять раз подряд.
Эта стандартная программа тестирует несколько значений ширины путем попытки различных ширин. Выбран набор испытательных ширин, равномерно распределенных между заданными начальными верхними и нижними границами. Ширина с самым низким значением log10 (GCV) выбрана. Область вокруг лучшей ширины затем тестируется более подробно — это упоминается как изменение масштаба. А именно, новая область значений испытательных ширин сосредоточена на лучшей ширине, найденной в предыдущей области значений, и длина интервала, из которого выбраны ширины, уменьшается до 2/5 длины интервала при предыдущем изменении масштаба. Прежде чем новый набор испытательных ширин тестируется, центральный выбор обновлен, чтобы отразить лучшую ширину и
найден до сих пор. Это может означать, что местоположение оптимальной ширины изменяется между изменениями масштаба из-за новых центральных местоположений.
Подходящие Параметры. Lambda selection algorithm — подходящий алгоритм Среднего уровня, из которого вы тестируете с различными испытательными значениями
. Значением по умолчанию является IterateRidge.
Number of trial widths in each zoom — Количество испытаний сделано при каждом изменении масштаба. Протестированные ширины равномерно распределены между начальными верхними и нижними границами. Значение по умолчанию равняется 10.
Number of zooms — Число раз вы увеличиваете масштаб. Значение по умолчанию равняется 5.
Initial lower bound on width — Нижняя граница на ширине для первого изменения масштаба. Значение по умолчанию 0.01.
Initial upper bound on width — Верхняя граница на ширине для первого изменения масштаба. Значение по умолчанию равняется 20.
Отображение Если вы устанавливаете этот флажок, диаграмма стебель-листья log10 (GCV) против ширины построена. Лучшая ширина отмечена зеленой звездочкой.
В алгоритме WidPerDim (Ширина На Размерность), обобщены радиальные основные функции. Вместо того, чтобы иметь один параметр ширины, различная ширина в каждом входном факторе может использоваться; то есть, кривые уровня являются эллиптическими, а не круговыми (или сферическими с большим количеством факторов). Основные функции больше не радиально симметричны.
Это может быть особенно полезно, когда сумма изменчивости значительно отличается по каждому входному направлению. Этот алгоритм предлагает больше гибкости, чем TrialWidths, но является более в вычислительном отношении дорогим.
Можно установить Initial width в средствах управления RBF на диалоговом окне Global Model Setup. Для большинства алгоритмов Initial width является одним значением. Однако для WidPerDim (доступный в выпадающем Width selection algorithm), можно задать вектор ширин, чтобы использовать в качестве стартовых ширин.
При предоставлении вектора ширин должен быть тот же номер как количество глобальных переменных, и они должны быть в том же порядке, как задано в плане тестирования. Если вы обеспечиваете одну ширину, то все размерности начинаются от той же начальной ширины, но, вероятно, переместятся оттуда в вектор ширин во время образцового подбора кривой.
Оценка времени для ширины на алгоритм размерности вычисляется. Это дано как много единиц измерения времени (когда это зависит от машины). Временная оценка более чем 10, но меньше чем 100 генерируют предупреждение. Временная оценка более чем 100 может занять предельно долгое количество времени (вероятно, более чем пять минут на большинстве машин). У вас есть опция, чтобы остановить выполнение и изменить некоторые параметры, чтобы уменьшать время выполнения.
Подходящие Параметры. Что касается алгоритма TrialWidths.
Существует три части к древовидному алгоритму регрессии для RBFs:
Древовидное Создание. Древовидный алгоритм регрессии создает дерево регрессии из данных и использует узлы (или панели) этого дерева, чтобы вывести центры кандидата и ширины для RBF. Корневая панель дерева соответствует гиперкубу, который содержит все точки данных. Эта панель разделена на две дочерних панели, таким образом, что каждый дочерний элемент содержит тот же объем изменения, так, как возможно. Дочерняя панель с большей частью изменения затем разделена похожим способом. Этот процесс продолжается, пока нет никаких панелей, оставленных разделению, т.е. никакая бездетная панель не имеет больше, чем минимальное количество точек данных, или пока максимальное количество панелей не было достигнуто. Каждая панель в дереве соответствует центру кандидата, и размер панели определяет ширину, которая идет с тем вектором.
Размер дочерних панелей может базироваться только на размере родительской панели или может быть определен путем уменьшения дочерней панели на данные, которые это содержит.
Если вы выбрали Radial Basis Function в диалоговом окне Global Model Setup, можно выбрать Tree Regression из Width Selection Algorithm выпадающее меню.
Нажмите Advanced, чтобы открыть Радиальное Окно параметров Основных функций, чтобы достигнуть настроек, таких как максимальное количество панелей и минимальное количество точек данных на панель. Чтобы уменьшить дочерние панели, чтобы соответствовать данным, выберите флажок Shrink panels to data.
Альфа-Алгоритм выбора. Размер для ширин кандидата не взят непосредственно из размеров панели: мы должны масштабировать размеры панели, чтобы получить соответствующие ширины. Этот масштабный коэффициент называется альфой. Тот же масштабный коэффициент должен быть применен к каждой панели в дереве и определить оптимальное значение альфы, мы используем альфа-алгоритм выбора.
Можно выбрать параметр Specify Alpha, чтобы задать точное значение альфы, чтобы использовать, или можно выбрать Trial Alpha. Trial Alpha очень похож на Испытательный алгоритм Ширин. Единственная разница - то, что испытательный альфа-алгоритм может задать, как расположить значения с интервалами, чтобы искать. Linear эквивалентен используемый испытательными ширинами, но Logarithmic ищет больше значений около более низкой области значений.
Нажмите Advanced, чтобы открыть Радиальное Окно параметров Основных функций, чтобы достигнуть дальнейших настроек, таких как границы на альфе, количестве изменений масштаба и количестве испытательных альф. Здесь можно установить флажок Display, чтобы видеть прогресс алгоритма, и значения альфы запоздали.
Центральный Алгоритм выбора. Древовидное создание генерирует центры кандидата, и альфа-выбор генерирует ширины кандидата для этих центров. Центральный выбор выбирает который из тех центров, чтобы использовать.
Generic Center Selection является центральным алгоритмом выбора, который знает, что ничто о древовидной структуре не используется. Это использует Rols, который является очень быстрым способом выбрать центры и работает в этом случае, а также обычные случаи RBF. Однако в этом случае кандидаты на центры не являются данными центрами от дерева регрессии.
Tree-based center selection использует дерево регрессии. Естественно использовать дерево регрессии, чтобы выбрать центры из-за способа, которым это создается. В частности, панель, соответствующая корневому узлу, должна быть рассмотрена для выбора перед любым из его дочерних элементов, когда это получает крупную деталь в то время как узлы в листах древовидных мелких деталей получения. Это - то, что делает Tree-based center selection. Можно также определить максимальный номер центров.
Нажмите Advanced, чтобы открыть Радиальное Окно параметров Основных функций, чтобы достигнуть установки Model selection criteria. Model selection criteria определяет, какая функция должна использоваться в качестве меры того, насколько хороший модель. Это может быть BIC (Байесов информационный критерий), или GCV (обобщил перекрестную валидацию). BIC обычно менее восприимчив к по подбору кривой.
Меню Stepwise является тем же самым для всего RBFs, смотрите Класс Глобальной модели: Радиальная Основная функция.
Древовидная Регрессия и CentreExchange являются единственными алгоритмами, которые разрешают центрам, которые не расположены в точках данных. Это означает, что вы не видите центры на образцовых графиках.
Если вы оставите Alpha selection algorithm в значении по умолчанию, Trial Alpha, вы будете видеть диалоговое окно прогресса, когда вы нажмете OK, чтобы начать моделировать. Пример показывают.
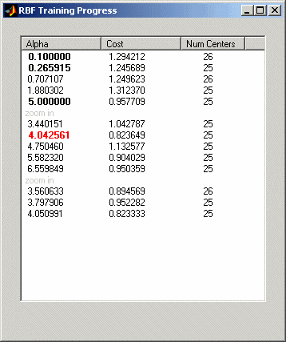
Это - диалоговое окно прогресса в качестве примера модели Tree Regression RBF, соответствующей происходящему. Здесь вы видите каждое испытательное значение альфы с его расчетной стоимостью и лучшим количеством центров с тем значением альфы. Альфа-значение красного цвета является лучшим до сих пор. Альфа-более не красные значения, но полужирным, предыдущие оптимальные значения. Можно затем совершенствовать модель путем увеличивания масштаб оптимальных значений для альфы и количества центров.
Ссылка: M. Орр, Дж. Халлэм, К. Тэкезоа, А. Мюррей, С. Ниномия, М. Оид, Т. Леонард, “Комбинируя деревья регрессии и радиальные сети основной функции”, международный журнал нейронных систем, издания 10, № 6 (2000) 453-465.
Можно использовать функцию Чернослива, чтобы сократить количество центров в радиальной сети основной функции. Это помогает вам решить, сколько центров необходимо.
Использовать средство Чернослива:
Выберите глобальную модель RBF в дереве модели.
Или нажмите кнопку на панели инструментов или выберите пункт меню Model> Utilities> Prune.
Количество диалогового окна Селектора Центров появляется.
Графики показывают, как подходящее качество сети растет, когда добавляется больше RBFs. Это использует то, что большинство центральных алгоритмов выбора является жадным по своей природе, и таким образом, порядок, в котором центры были выбраны примерно, отражает порядок важности основных функций.
Подходящие критерии по умолчанию являются логарифмами НАЖАТИЯ, GCV, RMSE и Взвешенного НАЖАТИЯ. Дополнительные опции определяются вашими выборами в итоговой Статистике. Взвешенное НАЖАТИЕ штрафует наличие большего количества центров, и выбор количества центров, чтобы минимизировать взвешенное НАЖАТИЕ часто является хорошим вариантом.
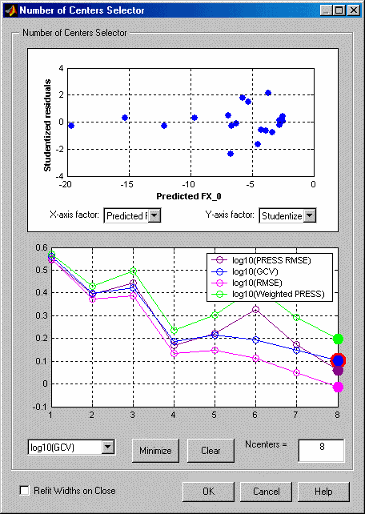
Все четыре критерия в этом типичном примере указывают на тот же минимум в восьми центрах.
Если графики все уменьшение, как в предыдущем примере, это предполагает, что максимальное количество центров является слишком маленьким, и число центров должно быть увеличено.
Нажатие кнопки Minimize выбирает количество центров, которое минимизирует критерий, выбранный в выпадающем меню слева. Хорошо, если это значение также минимизирует все другие критерии. Кнопка Clear возвращается к предыдущему выбору.
Обратите внимание на то, что сокращение количества центров с помощью Чернослива только переоборудует линейные параметры (веса RBF). Нелинейные параметры (центральные местоположения, ширина и lambda) не настроены. Можно выполнить дешевый ремонт ширины при выходе из диалогового окна путем установки флажка Refit widths on close. Если сеть была значительно сокращена, необходимо использовать кнопку на панели инструментов Update Model Fit. Это выполняет полный ремонт всех параметров.
Позвольте A быть матрицей, таким образом, что веса даны тем
, где X матрица регрессии. Форма A отличается в зависимости от основного подходящего используемого алгоритма.
В случае обычных наименьших квадратов мы имеем = X'X.
Для гребенчатой регрессии (с параметром регуляризации
), A дан = X'X + 
я
Затем алгоритм Rols. Во время алгоритма Rols X анализируется с помощью Алгоритма Грама-Шмидта, чтобы дать X = WB, где W имеет ортогональные столбцы, и B верхний треугольный. Соответствующая матрица А для Rols затем
.
Матрица
называется матрицей шляпы, и рычаги ith точки данных привет даны ith диагональным элементом H. Все статистические данные, выведенные из матрицы шляпы, например, НАЖАТИЯ, studentized невязки, доверительные интервалы, и расстояние Кука, вычисляются с помощью матрицы шляпы, соответствующей конкретному подходящему алгоритму.
Так же PEV, данный в Терминах Тулбокса и Определениях Статистики как
становится
PEV вычисляется с помощью формы соответствующего конкретному подходящему алгоритму (обычные наименьшие квадраты, гребень или списки).
Обобщенная перекрестная проверка (GCV) является мерой качества подгонки модели к данным, которые минимизированы, когда невязки маленькие, но не столь маленькими, что сеть сверхсоответствовала данным. Легко вычислить, и сети с маленькими значениями GCV должны иметь хорошую прогнозирующую возможность. Это связано со статистической величиной НАЖАТИЯ.
Определение GCV дано Орром (4, смотрите Ссылки).
где y является целевым вектором, N является количеством наблюдений, и P является матрицей проекции, данной мной - XA-1XT. Смотрите Статистику для определения A.
Важной функцией использования GCV как критерий определения оптимальной сети в наших подходящих алгоритмах является существование формул обновления для параметра регуляризации
. Эти формулы обновления получены путем дифференциации GCV относительно
и обнуления результата. Таким образом, они основаны на спуске градиента.
Это дает общее уравнение (из Орра, 6, Ссылки)
Мы теперь специализируем эти формулы к случаю гребенчатой регрессии и к алгоритму Rols.
Это показывают в Орре (4) и утверждают в Орре (5, смотрите Ссылки), что для случая гребенчатой регрессии GCV может быть записан как
где
“эффективное количество параметров”, которым дан
где NumTerms является количеством условий, включенных в модель.
Для RBFs 'p' является эффективным количеством параметров, то есть, количеством условий минус корректировка, чтобы учесть эффект сглаживания lambda в алгоритме подбора. Когда lambda = 0, эффективное количество параметров совпадает с количеством условий.
Формула для обновления
дана
где 
На практике предыдущие формулы не используются явным образом в Орре (5, смотрите Ссылки). Вместо этого сингулярное разложение X сделано, и формулы переписаны с точки зрения собственных значений и собственных векторов матрицы XX'. Это старается не брать инверсию матрицы А, и это может использоваться, чтобы дешево вычислить GCV для многих значений
. Смотрите Статистику для определения A.
В случае Rols, компонентов для формулы
вычисляются с помощью формул, данных в Орре [6; смотрите Ссылки]. Вспомните, что матрица регрессии учтена во время алгоритма Rols в продукт X = WB. Позвольте wj обозначить jth столбец W, затем мы имеем
и “эффективным количеством параметров” дают
Это эквивалентно 'p' (эффективное количество параметров) заданный в GCV для Гребенчатой Регрессии.
Формула переоценки для
дана
где дополнительно
и
Обратите внимание на то, что эти формулы для Rols не требуют явной инверсии A. Смотрите Статистику для определения A.
Чен, S., Chng, E.S., Alkadhimi, Упорядоченный Ортогональный Алгоритм Наименьших квадратов для Построения Радиальных Сетей Основной функции, Инта Дж. Контрола, 1996, Издание 64, № 5, стр 829-837.
Hassoun, M., основные принципы искусственных нейронных сетей, MIT, 1995.
Орр, M., Введение в Радиальные Сети Основной функции, доступные под эгидой http://www.anc.ed.ac.uk/.
Орр, M., Оптимизируя Ширины Радиальных Основных функций, доступных под эгидой http://www.anc.ed.ac.uk/.
Орр, M., Регуляризация в Выборе Радиальных Центров Основной функции, доступных под эгидой http://www.anc.ed.ac.uk/.
Wendland, H., Кусочные полиномы, Положительные Определенные и Сжато Поддерживаемые Радиальные Основные функции Минимальной Степени, Усовершенствований в Вычислительной Математике 4 (1995), стр 389-396.
Гибридные RBFs комбинируют радиальную модель основной функции с более стандартными линейными моделями, такими как полиномы или гибридные сплайны. Эти две части добавляются вместе, чтобы сформировать полную модель. Этот подход предлагает способность объединить априорное знание, такое как ожидание квадратичного поведения в одной из переменных, с непараметрической природой RBFs.
Образцовый графический интерфейс пользователя настройки для гибридного RBFs имеет главную кнопку Set Up , где можно установить алгоритм подбора и опции. Интерфейс также имеет две вкладки, один, чтобы задать радиальную часть основной функции, и один для линейной образцовой части.
Это - тот же алгоритм, как используется в обычном RBFs, то есть, ведомый поиск лучшего параметра ширины.
Этот алгоритм является обобщением StepItRols для RBFs. Алгоритм выбирает радиальные основные функции и линейные образцовые условия чересстрочным способом, а не на двух шагах. На каждом шаге прямая поисковая процедура выполняется, чтобы выбрать радиальную основную функцию (с центром, выбранным из набора точек данных) или линейный образцовый термин (выбранный от тех заданных в линейной образцовой панели настройки), который уменьшает упорядоченную ошибку больше всего. Этот процесс продолжается, пока максимальное количество условий не выбрано. Первые несколько условий добавляются с помощью хранимой суммы lambda, пока Number of terms to add before updating не был достигнут. Впоследствии lambda выполнен с помощью итераций после того, как каждый центр добавляется, чтобы улучшить GCV.
Подходящие опции для этого алгоритма следующие:
Максимальное количество Maximum number of terms: условий, которые будут выбраны. Значением по умолчанию является количество точек данных.
Максимальное количество Maximum number of centers: условий, которые могут быть радиальными основными функциями. Значением по умолчанию является четверть точек данных, или 25, какой бы ни меньше.
Максимальное количество использованных терминов является комбинацией максимального количества центров и количества линейных образцовых условий. Это ограничивается можно следующим образом:
Максимальное количество терминов, использованных = Минимум (Maximum number of terms, Maximum number of centers + количество линейных образцовых условий)
В результате этого модель может иметь больше центров, чем заданный в Maximum number of centers, но всегда будет меньше условий, чем (Maximum number of centers + количество линейных образцовых условий). Можно просмотреть количество возможных линейных образцовых условий на вкладке Linear Part диалогового окна Global Model Setup (Total number of terms).
Процент Percentage of data to be candidate centers: точек данных, которые доступны, чтобы быть выбранными в качестве центров. Значение по умолчанию составляет 100%, когда количество точек данных 200.
Number of terms to add before updating:, Сколько условий, чтобы добавить прежде, чем обновить lambda начинается.
Допуск Minimum change in log10(GCV):.
Количество Maximum no. times log10(GCV) change is minimal: шагов подряд, что изменение в log10 (GCV) может быть меньше, чем допуск перед алгоритмом, останавливается.
Этот алгоритм запускается путем подбора кривой линейной модели, заданной в линейной образцовой панели, и затем соответствует радиальной сети основной функции к невязке. Можно задать линейные образцовые условия, чтобы включать в обычный способ использовать термин селектор. При желании можно активировать пошаговые опции. В этом случае, после того, как линейная образцовая часть адаптирована, некоторые условия автоматически добавлены или удалены, прежде чем часть RBF адаптирована. Можно выбрать алгоритм и опции, которые используются, чтобы соответствовать нелинейным параметрам RBF путем нажатия кнопки Set Up в опциях обучения RBF.
Определите, какие параметры оказывают большую часть влияния на подгонку путем выполнения этих шагов:
Соответствуйте RBF по умолчанию. Удалите любые очевидные выбросы.
Получите общее представление о том, сколько RBFs будет необходимыми. Если центр совпадает с точкой данных, он отмечен пурпурной звездочкой на, Предсказывал/Наблюдал график. Можно просмотреть местоположение центров в графическом и формате таблицы при помощи кнопки на панели инструментов View Centers
. Если вы удаляете выброс, который совпал с центром (отмеченный звездочкой), ремонт путем нажатия на Update Fit на панели инструментов.
Попробуйте больше чем одним ядром. Можно изменить параметры в подгонке путем нажатия кнопки Set Up в диалоговом окне Model Selection.
Выберите основной алгоритм выбора ширины. Попробуйте и TrialWidths и алгоритмами WidPerDim.
Определите, какие типы ядра выглядят самыми обнадеживающими.
Сузьте соответствующую область значений ширины, чтобы искать.
Выберите центральный алгоритм выбора.
Выберите алгоритм выбора lambda.
Попытайтесь изменить параметры в алгоритмах.
Если какие-либо точки, кажется, возможные выбросы, попытайтесь соответствовать модели и и без тех точек.
Если на каком-либо этапе вы выбираете изменение, которое оказывает большое влияние (такое как удаление выброса), то необходимо повторить предыдущие шаги, чтобы определить, влияло ли это на путь, вы выбрали.
Смотрите Подходящие Стандартные программы для деталей обо всех подходящих параметрах.
Model Browser имеет быструю опцию для сравнения всех различных ядер RBF и попытки множества цифр центров.
После подбора кривой RBF по умолчанию выберите глобальную модель RBF в дереве модели.
Кликните по значку панели инструментов Build Models.
Выберите значок RBF в диалоговом окне Build Models, которое появляется, и нажмите OK.
Окно параметров Построения моделей появляется. Можно задать область значений значений для максимального количества центров и нажать Model settings, чтобы изменить любые другие образцовые настройки. Используемые значения по умолчанию совпадают с родительским типом модели RBF.
Можно установить флажок к Build all kernels, чтобы создать модели с заданной областью значений центров каждого типа ядра как выбор дочерних вершин текущей модели RBF.
Обратите внимание, что это может занять много времени для локальных моделей, когда вы создадите альтернативные модели с областью значений центров каждого типа ядра для каждой функции ответа; если построение моделей запускается, можно всегда нажимать Stop, чтобы прерваться, если процесс занимает слишком много времени.
Нажмите Build, чтобы создать заданные модели.
Основной параметр, который необходимо настроить в порядке получить подходящий вариант для RBF, является максимальным количеством центров. Это - параметр центрального алгоритма выбора и является максимальным количеством centers/RBFs, который выбран.
Обычно максимальное количество центров является количеством RBFs, которые на самом деле выбраны. Однако иногда меньше RBFs выбрано, потому что (упорядоченная) ошибка упала ниже допуска, прежде чем максимум был достигнут.
Необходимо использовать много RBFs, который является значительно меньше, чем количество точек данных, в противном случае существует недостаточно степеней свободы по ошибке оценить прогнозирующее качество модели. Таким образом, вы не можете сказать, полезна ли модель, если вы используете слишком много RBFs. Мы рекомендовали бы верхнюю границу 60% на отношении количества RBFs к количеству точек данных. Наличие 80 центров, когда существует только 100 точек данных, может казаться, дает хорошее значение НАЖАТИЯ, но когда дело доходит до валидации, может иногда становиться ясно, что данные были сверхадаптированы, и прогнозирующая возможность не так хороша, как НАЖАТИЕ предложило бы.
Одна стратегия выбора количества RBFs состоит в том, чтобы соответствовать большему количеству центров, чем вы думаете, необходим (скажите 70 из 100), затем используйте кнопку на панели инструментов Prune, чтобы сократить количество центров в модели. После сокращения сети обратите внимание на сокращенное количество RBFs. Попытайтесь соответствовать модели снова максимальным количеством набора центров к этому сокращенному количеству. Это повторно вычисляет значения нелинейных параметров (ширина и lambda), чтобы быть оптимальным для сокращенного количества RBFs.
Одна стратегия использования Пошаговых состоит в том, чтобы использовать его, чтобы минимизировать НАЖАТИЕ как итоговую подстройку для сети, если сокращение было сделано. Принимая во внимание, что Чернослив только позволяет последний RBF, введенный, чтобы быть удаленным, Пошагово позволяет любому RBF быть вынутым.
Не фокусируйтесь только на НАЖАТИИ как мера качества подгонки, особенно в больших отношениях RBFs к точкам данных. Возьмите log10 (GCV) во внимание также.
Попробуйте и TrialWidths и WidPerDim. Второй алгоритм предлагает больше гибкости, но является более в вычислительном отношении дорогим. Просмотрите значения ширины в каждом направлении, чтобы видеть, существует ли значительная разница, чтобы видеть, стоит ли это фокусировать, усилие на эллиптических основных функциях (используйте кнопку на панели инструментов View Model
).
Если со множеством основных функций ширины значительно не отличаются между размерностями, и значения PRESS/GCV не значительно улучшены с помощью WidPerDim по TrialWidths, то фокусируются на TrialWidths, и только возвращаются к WidPerDim, чтобы подстроить в заключительных этапах.
Включите опцию Display в TrialWidths, чтобы видеть прогресс алгоритма. См. за альтернативными областями в области значений ширины, которыми преждевременно пропустили. Вывод log10 (GCV) в итоговом изменении масштаба должен быть подобным для каждой из ширин, которые попробовали; то есть, вывод должен быть приблизительно плоским. Если дело обстоит не так, попытайтесь увеличить число изменений масштаба.
В TrialWidths, для каждого типа RBF, попытка сузить начальную область значений ширин, чтобы искать. Эта сила позволяет количеству изменений масштаба уменьшаться.
Трудно дать эмпирические правила о том, как выбрать лучший RBF, когда лучший выбор очень информационно-зависим. Лучшая инструкция должна попробовать всех их и алгоритмами верхнего уровня (TrialWidths и WidPerDim) и разумным количеством центров, сравнить значения PRESS/GCV, затем фокусировать на тех тот самый обнадеживающий взгляд.
Если мультиквадрики и сплайны тонкой пластины дают плохие результаты, стоит судить их в сочетании с полиномами младшего разряда как гибридный сплайн. Попытайтесь добавить мультиквадрики с постоянным термином и сплайны тонкой пластины с линейным (порядок 1) условия. Смотрите Гибридные Радиальные Основные функции.
Не упустите создание условий проблем с Гауссовыми ядрами (скажите номер условия> 10^8).
Не упустите странные результаты с функциями Вендлэнда, когда отношение количества параметров к количеству наблюдений будет высоко. Когда эти функции имеют очень маленькую ширину, каждая основная функция только способствует подгонке в одной точке данных. Это вызвано тем, что его поддержка только охватывает одну основную функцию, которая является его центром. Невязки будут нулем в каждой из точек данных, выбранных в качестве центра и больших в других точках данных. Этот сценарий может указать на хорошие значения RMSE, но прогнозирующее качество сети будет плохо.
Lambda является параметром регуляризации.
IterateRols обновляет центры после каждого обновления lambda. Это делает его более в вычислительном отношении интенсивным, но потенциально приводит к лучшей комбинации lambda и центров.
StepItRols чувствителен к установке Number of centers to add before updating. Включите опцию Display, чтобы просмотреть, как log10 (GCV) уменьшает, когда количество центров растет.
Исследуйте графики, произведенные из алгоритма выбора lambda, игнорирование предупреждения “Чрезмерного количества графиков будет произведено”. Был бы, увеличивая допуск или количество начальных тестовых значений для вывода lambda к лучшему выбору lambda?
На большинстве проблем Rols, кажется, является самым эффективным.
Если меньше, чем максимальное количество центров выбираются, и вы хотите обеспечить выбор максимального количества, уменьшать допуск до эпсилона (eps).
CenterExchange является очень дорогим, и вы не должны использовать это на больших проблемах. В этом случае другие центральные алгоритмы выбора, которые ограничивают центры, чтобы быть подмножеством точек данных, не могут предложить достаточную гибкость.
Попробуйте Пошагово после сокращения, затем обновите образцовую подгонку с новым максимальным количеством набора центров к количеству условий, оставленных после Пошагово.
Обновите образцовую подгонку после удаления выбросов; используйте кнопку на панели инструментов.
Перейдите к линейной части, разделяют на области и задают полином или условия сплайна, которые вы ожидаете видеть в модели.
Подбор кривой слишком многим условиям non-RBF сделан очевидным большим значением lambda, указав, что базовые тренды заботятся о линейной частью. В этом случае необходимо сбросить начальное значение lambda (чтобы сказать 0.001) перед следующей подгонкой.
С любой моделью можно использовать кнопку на панели инструментов View Model или View> Model Definition (или горячая клавиша CTRL +V), чтобы видеть детали текущей модели. Диалоговое окно Model Viewer появляется. Здесь для любой модели RBF вы видите тип ядра, количество центров, ширины и параметра регуляризации.
Однако, чтобы задать формулу модели RBF полностью, также необходимо дать местоположения центров и высоту каждой основной функции. Центральная информация о местоположении доступна в диалоговом окне “View Centers”, и коэффициенты могут быть найдены в окне “Stepwise”. Обратите внимание, что эти значения - все в закодированных модулях.
