Много решателей позволяют вам предоставлять функцию, которая вычисляет первые производные (градиенты или Якобианы) ограничительных функций или цели. Можно проверять ли производные, вычисленные функциональными приближениями конечной разности соответствия. Эта проверка может помочь вам диагностировать, правильна ли ваша производная функция.
Если компонент функции градиента является меньше, чем 1, “соответствие” означает абсолютную разность функции градиента, и приближение конечной разности того компонента является меньше, чем 1e-6.
В противном случае “соответствие” означает, что относительной разницей являются меньше, чем 1e-6.
Опция CheckGradients заставляет решатель проверять предоставленную производную по приближению конечной разности во всего одной точке. Если конечная разность и предоставленные производные не соответствуют, ошибки решателя. Если соответствие производных к в 1e-6, решатель сообщает о расчетных различиях и продолжает выполнять итерации без дальнейших производных проверок. Решатели проверяют соответствие в точке, которая является небольшим случайным возмущением начальной точки x0, измененный, чтобы быть в любых границах. Решатели не включают вычисления для CheckGradients в функциональном количестве; смотрите Итерации и Функциональные количества.
В командной строке MATLAB®:
Установите SpecifyObjectiveGradient или опции SpecifyConstraintGradient к true с помощью optimoptions. Убедитесь ваша цель или ограничительные функции предоставляют соответствующие производные.
Установите опцию CheckGradients на true.
Используя приложение Оптимизации:
В панели Problem Setup and Results выберите Derivatives: Objective function: Gradient supplied или Nonlinear constraint function: Derivatives: Gradient supplied. Убедитесь ваша цель или ограничительные функции предоставляют соответствующие производные.
В панели Options проверяйте User-supplied derivatives > Validate user-supplied derivatives
Центральные конечные разности более точны, чем прямые конечные разности по умолчанию. Использовать центральные конечные разности:
В командной строке MATLAB, набор опция FiniteDifferenceType к 'central' с помощью optimoptions.
Используя приложение Оптимизации, в панели Approximated derivatives, устанавливает Type на central differences.
Полагайте, что проблема минимизации Функции Розенброка в единичном диске, как описано в Решает Ограниченную Нелинейную проблему, Основанную на решателе. Функция rosenboth вычисляет целевую функцию и ее градиент:
function [f g H] = rosenboth(x)
f = 100*(x(2) - x(1)^2)^2 + (1-x(1))^2;
if nargout > 1
g = [-400*(x(2)-x(1)^2)*x(1)-2*(1-x(1));
200*(x(2)-x(1)^2)];
if nargout > 2
H = [1200*x(1)^2-400*x(2)+2, -400*x(1);
-400*x(1), 200];
end
endrosenboth вычисляет Гессиан также, но этот пример не использует Гессиан.
Функция unitdisk2 правильно вычисляет ограничительную функцию и ее градиент:
function [c,ceq,gc,gceq] = unitdisk2(x)
c = x(1)^2 + x(2)^2 - 1;
ceq = [ ];
if nargout > 2
gc = [2*x(1);2*x(2)];
gceq = [];
endФункция unitdiskb неправильно вычисляет градиент ограничительной функции:
function [c ceq gc gceq] = unitdiskb(x)
c = x(1)^2 + x(2)^2 - 1;
ceq = [ ];
if nargout > 2
gc = [x(1);x(2)]; % Gradient incorrect: off by a factor of 2
gceq = [];
endУстановите опции использовать алгоритм внутренней точки, градиент цели и ограничительных функций и опции CheckGradients:
% For reproducibility--CheckGradients randomly perturbs the initial point
rng(0,'twister');
options = optimoptions(@fmincon,'Algorithm','interior-point',...
'CheckGradients',true,'SpecifyObjectiveGradient',true,'SpecifyConstraintGradient',true);Решите минимизацию с fmincon с помощью ошибочной ограничительной функции unitdiskb:
[x fval exitflag output] = fmincon(@rosenboth,...
[-1;2],[],[],[],[],[],[],@unitdiskb,options);
____________________________________________________________
Derivative Check Information
Objective function derivatives:
Maximum relative difference between user-supplied
and finite-difference derivatives = 1.84768e-008.
Nonlinear inequality constraint derivatives:
Maximum relative difference between user-supplied
and finite-difference derivatives = 1.
User-supplied constraint derivative element (2,1): 1.99838
Finite-difference constraint derivative element (2,1): 3.99675
____________________________________________________________
Error using validateFirstDerivatives
Derivative Check failed:
User-supplied and forward finite-difference derivatives
do not match within 1e-006 relative tolerance.
Error in fmincon at 805
validateFirstDerivatives(funfcn,confcn,X, ...Ограничительная функция не совпадает с расчетным градиентом, поощряя вас проверять функцию на ошибку.
Замените ограничительную функцию unitdiskb на unitdisk2 и запустите минимизацию снова:
[x fval exitflag output] = fmincon(@rosenboth,... [-1;2],[],[],[],[],[],[],@unitdisk2,options); ____________________________________________________________ Derivative Check Information Objective function derivatives: Maximum relative difference between user-supplied and finite-difference derivatives = 1.28553e-008. Nonlinear inequality constraint derivatives: Maximum relative difference between user-supplied and finite-difference derivatives = 1.46443e-008. Derivative Check successfully passed. ____________________________________________________________ Local minimum found that satisfies the constraints...
Приложение Оптимизации предупреждает, что будет удалено в будущем релизе.
Настраивать пример с помощью правильных производных функций, но начиная с [0 0], с помощью приложения Оптимизации:
Запустите приложение Оптимизации путем ввода optimtool в командной строке.
Установите панель Problem Setup and Results совпадать со следующей фигурой:
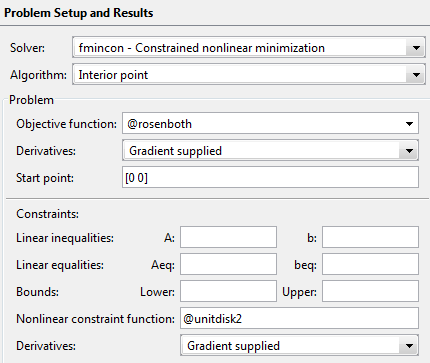
Установите панель Options совпадать со следующей фигурой:
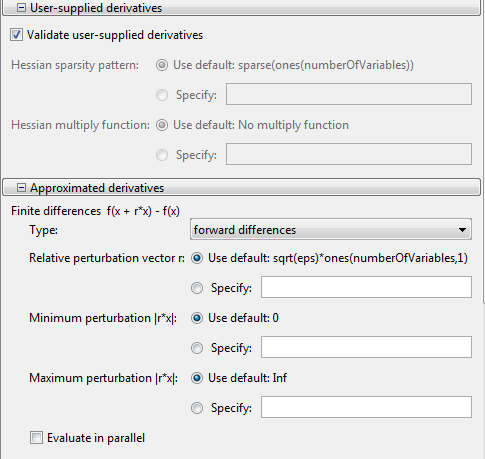
Нажмите кнопку Start под Run solver and view results.
Выходные отображения на экране
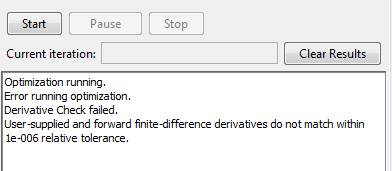
Прямое приближение конечной разности достаточно неточно около [0 0], который приводит к сбою производная проверка.
Чтобы использовать более точные центральные различия, выберите central differences в панели Approximated derivatives > Type:
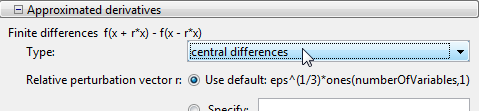
Нажмите Run solver and view results > Clear Results, затем Start. На этот раз производная проверка успешна:
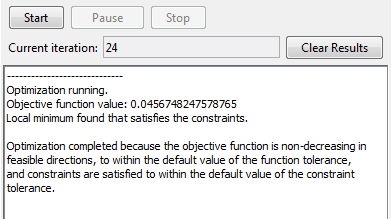
Производная проверка также успешно выполняется, когда вы выбираете начальную точку [-1 2] или наиболее случайные точки.