Алгоритм Внутренней точки fmincon с Аналитическим Гессианом

Алгоритм внутренней точки fmincon может принять функцию Гессиана как вход. Когда вы предоставляете Гессиан, можно получить более быстрое, более точное решение ограниченной проблемы минимизации.

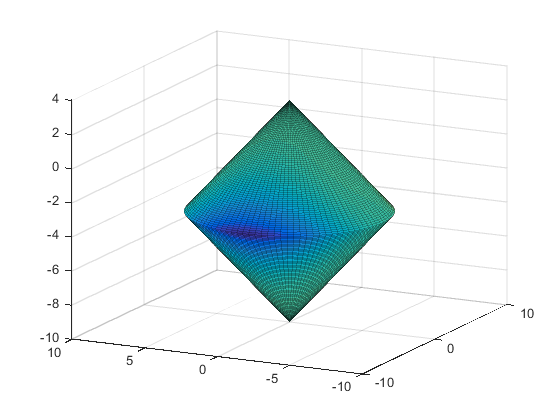
Ограничительный набор для этого примера является пересечением внутренней части двух конусов — одно подчеркивание и одно обращение вниз. Ограничительная функция c является двухкомпонентным вектором, одним компонентом для каждого конуса. Поскольку это - 3D пример, градиент ограничения, которое c 3 2 матрица.

function [c ceq gradc gradceq] = twocone(x)
% This constraint is two cones, z > -10 + r
% and z < 3 - r

ceq = [];
r = sqrt(x(1)^2 + x(2)^2);
c = [-10+r-x(3);
    x(3)-3+r];

if nargout > 2

    gradceq = [];
    gradc = [x(1)/r,x(1)/r;
       x(2)/r,x(2)/r;
       -1,1];

end

Целевая функция становится быстро отрицательной, когда координата x(1) становится отрицательной. Его градиент является трехэлементным вектором.

function [f gradf] = bigtoleft(x)
% This is a simple function that grows rapidly negative
% as x(1) gets negative
%
f=10*x(1)^3+x(1)*x(2)^2+x(3)*(x(1)^2+x(2)^2);

if nargout > 1

   gradf=[30*x(1)^2+x(2)^2+2*x(3)*x(1);
       2*x(1)*x(2)+2*x(3)*x(2);
       (x(1)^2+x(2)^2)];

end

Вот график проблемы. Штриховка представляет значение целевой функции. Вы видите, что целевая функция минимизирована около x = [-6.5,0,-3.5]:

Код для генерации фигуры

function createfigure2

% Create figure
figure1 = figure;

% Create axes
axes1 = axes('Parent',figure1);
view([-63.5 18]);
grid('on');
hold('all');

%Set up polar coordinates and two cones
r=0:.1:6.5;
th=2*pi*(0:.01:1);
x=r'*cos(th);
y=r'*sin(th);
z=-10+sqrt(x.^2+y.^2);
zz=3-sqrt(x.^2+y.^2);

%evaluate objective function on cone surfaces
newxf=reshape(bigtoleft2([reshape(x,6666,1),reshape(y,6666,1),reshape(z,6666,1)]),66,101)/3000;
newxg=reshape(bigtoleft2([reshape(x,6666,1),reshape(y,6666,1),reshape(zz,6666,1)]),66,101)/3000;

% Create lower surf with color set by objective
surf(x,y,z,newxf,'Parent',axes1,'EdgeAlpha',0.25);

% Create upper surf with color set by objective
surf(x,y,zz,newxg,'Parent',axes1,'EdgeAlpha',0.25);

Функциональный bigtoleft2 векторизован:

function f = bigtoleft2(x)
%
f=10*x(:,1).^3+x(:,1).*x(:,2).^2+x(:,3).*(x(:,1).^2+x(:,2).^2);

Гессиан функции Лагранжа дан уравнением:

$\nabla_{x x}^{2} L (x, λ) = \nabla^{2} f (x) + \sum λ_{i} \nabla^{2} c_{i} (x) + \sum λ_{i} \nabla^{2} c e q_{i} (x) .$

Следующая функция вычисляет Гессиан в точке x со структурой множителя Лагранжа lambda:

function h = hessinterior(x,lambda)

h = [60*x(1)+2*x(3),2*x(2),2*x(1);
    2*x(2),2*(x(1)+x(3)),2*x(2);
    2*x(1),2*x(2),0];% Hessian of f
r = sqrt(x(1)^2+x(2)^2);% radius
rinv3 = 1/r^3;
hessc = [(x(2))^2*rinv3,-x(1)*x(2)*rinv3,0;
    -x(1)*x(2)*rinv3,x(1)^2*rinv3,0;
    0,0,0];% Hessian of both c(1) and c(2)
h = h + lambda.ineqnonlin(1)*hessc + lambda.ineqnonlin(2)*hessc;

Запустите эту проблему с помощью алгоритма внутренней точки в fmincon. Сделать это использование приложения Оптимизации:

Установите проблему как в следующей фигуре.
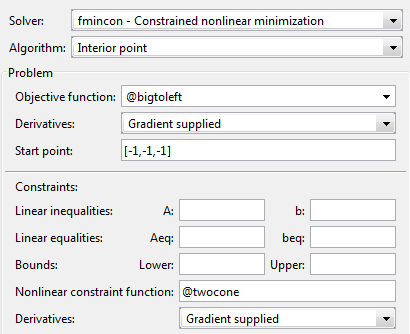
Для итеративного вывода прокрутка к нижней части Options разделяет на области и выбирает Level of display, iterative.
В панели Options дайте аналитический указатель на функцию Гессиана.
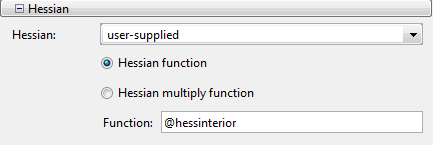
Под Run solver and view results нажмите Start.

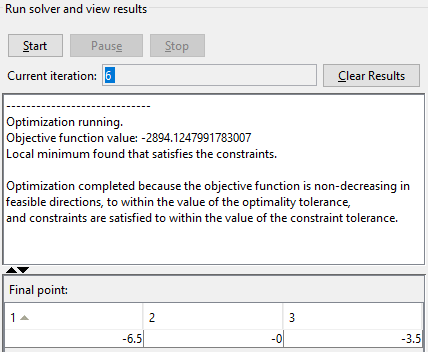
Выполнять минимизацию в командной строке:

Установите options можно следующим образом:

options = optimoptions(@fmincon,'Algorithm','interior-point',...
        'Display','off','SpecifyObjectiveGradient',true,'SpecifyConstraintGradient',true,...
        'HessianFcn',@hessinterior);

Запустите fmincon с отправной точкой [–1, –1, –1], с помощью структуры options:
```
[x,fval,mflag,output] = fmincon(@bigtoleft,[-1,-1,-1],...
           [],[],[],[],[],[],@twocone,options);
```

Исследуйте решение, значение целевой функции, выходной флаг и количество функциональных оценок и итераций:

x,fval,mflag,output.funcCount,output.iterations
x =

   -6.5000   -0.0000   -3.5000


fval =

  -2.8941e+03


mflag =

     1


ans =

     7


ans =

     6

Если вы не используете функцию Гессиана, fmincon берет 9 итераций, чтобы сходиться, вместо 6:

options = optimoptions(@fmincon,'Algorithm','interior-point',...
        'Display','off','SpecifyObjectiveGradient',true,'SpecifyConstraintGradient',true);

[x fval mflag output]=fmincon(@bigtoleft,[-1,-1,-1],...
           [],[],[],[],[],[],@twocone,options);

x,output.funcCount,output.iterations

x =

   -6.5000   -0.0000   -3.5000


ans =

    13


ans =

     9

Оба вывода выполнений к аналогичным решениям, но F-количество и количество итераций ниже при использовании аналитического Гессиана.

Документация

Алгоритм Внутренней точки fmincon с Аналитическим Гессианом

Похожие темы

Документация Optimization Toolbox

Поддержка