Наименьшие квадраты, в целом, являются проблемой нахождения векторного x, который является локальным минимизатором к функции, которая является суммой квадратов, возможно подвергните некоторым ограничениям:
таким образом, что A·x ≤ b, Aeq·x = beq, lb ≤ x ≤ ub.
Существует несколько решателей Optimization Toolbox™, доступных для различных типов F (x) и различные типы ограничений:
| Решатель | F (x) | Ограничения |
|---|---|---|
mldivide | C· – d | 'none' |
lsqnonneg | C· – d | x ≥ 0 |
lsqlin | C· – d | Связанный, линейный |
lsqnonlin | Общий F (x) | Связанный |
lsqcurvefit | F (x, xdata) – ydata | Связанный |
Существуют алгоритмы на четыре наименьших квадрата в решателях Optimization Toolbox, в дополнение к алгоритмам, используемым в mldivide:
Все алгоритмы являются крупномасштабными; смотрите Крупномасштабный по сравнению с Алгоритмами Средней шкалы. Для общего обзора методов нелинейного метода наименьших квадратов смотрите Денниса [8]. Определенные детали о методе Levenberg-Marquardt могут быть найдены в Moré [28].
Многие методы, используемые в решателях Optimization Toolbox, основаны на доверительных областях, простой все же мощной концепции в оптимизации.
Чтобы понять подход доверительной области к оптимизации, рассмотрите проблему безусловной минимизации, минимизируйте f (x), где функция берет аргументы вектора и возвращает скаляры. Предположим, что вы - в точке x в n - пробел, и вы хотите улучшиться, т.е. переместиться в точку с более низким значением функции. Основная идея состоит в том, чтобы аппроксимировать f с более простым функциональным q, который обоснованно отражает поведение функционального f в окружении N вокруг точки x. Это окружение является доверительной областью. Испытательный шаг s вычисляется путем минимизации (или приблизительно минимизации) по N. Это - подпроблема доверительной области,
| (1) |
Текущая точка обновляется, чтобы быть x + s если f (x + s) < f (x); в противном случае текущая точка остается неизменной, и N, область доверия, уменьшается, и испытательное вычисление шага повторяется.
Ключевые вопросы в определении определенного подхода доверительной области к минимизации f (x) состоят в том, как выбрать и вычислить приближение q (заданный в текущей точке x), как выбрать и изменить доверительную область N, и как точно решить подпроблему доверительной области. Этот раздел фокусируется на неограниченной проблеме. Более поздние разделы обсуждают дополнительные осложнения из-за присутствия ограничений на переменные.
В стандартном методе доверительной области ([48]), квадратичное приближение q задан первыми двумя сроками приближения Тейлора к F в x; окружение N является обычно сферическим или эллипсоидальным в форме. Математически подпроблема доверительной области обычно утверждается
| (2) |
где g является градиентом f в текущей точке x, H является матрицей Гессиана (симметрическая матрица вторых производных), D является диагональной матрицей масштабирования, Δ является положительной скалярной величиной и ∥. ∥ является 2-нормой. Хорошие алгоритмы существуют для решения уравнения 2 (см. [48]); такие алгоритмы обычно включают вычисление всех собственных значений H, и процесс Ньютона применился к характеристическому уравнению
Такие алгоритмы предоставляют точное решение уравнения 2. Однако они требуют времени, пропорционального нескольким факторизациям H. Поэтому для проблем доверительной области другой подход необходим. Несколько приближений и эвристических стратегий, на основе уравнения 2, были предложены в литературе ([42] и [50]). Подход приближения, сопровождаемый в решателях Optimization Toolbox, должен ограничить подпроблему доверительной области двумерным подпространством S ([39] и [42]). Однажды подпространство S был вычислен, работа, чтобы решить уравнение 2 тривиальна, даже если полная информация о собственном значении/собственном векторе необходима (поскольку в подпространстве, проблема только двумерна). Доминирующая работа теперь переключила к определению подпространства.
Двумерное подпространство S определяется при помощи предобусловленного процесса метода сопряженных градиентов, описанного ниже. Решатель задает S как линейный пробел, заполненный s 1 и s 2, где s 1 является в направлении градиента g, и s 2 является любой аппроксимированным направлением Ньютона, т.е. решением
| (3) |
или направление отрицательного искривления,
| (4) |
Философия позади этого выбора S должна обеспечить глобальную сходимость (через направление быстрейшего спуска или отрицательное направление искривления) и достигнуть быстро локальной сходимости (через шаг Ньютона, когда это существует).
Эскиз безусловной минимизации с помощью идей доверительной области теперь легко дать:
Сформулируйте двумерную подпроблему доверительной области.
Решите уравнение 2, чтобы определить испытательный шаг s.
Если f (x + s) <f (x), то x = x + s.
Настройте Δ.
Эти четыре шага повторяются до сходимости. Размерность доверительной области Δ настроена согласно стандартным правилам. В частности, это уменьшено, если испытательный шаг не принят, т.е. f (x + s) ≥ f (x). См. [46] и [49] для обсуждения этого аспекта.
Решатели Optimization Toolbox обрабатывают несколько важных особых случаев f со специализированными функциями: нелинейный метод наименьших квадратов, квадратичные функции и линейный метод наименьших квадратов. Однако базовые алгоритмические идеи эквивалентны для общего случая. Эти особые случаи обсуждены в более поздних разделах.
Важный особый случай для f (x) является проблемой нелинейного метода наименьших квадратов
| (5) |
где F (x) является функцией с векторным знаком с i компонента F (x), равный fi (x). Основной метод, используемый, чтобы решить эту проблему, эквивалентен в общем случае, описанном в Методах Доверительной области для Нелинейной Минимизации. Однако структура проблемы нелинейного метода наименьших квадратов используется, чтобы улучшить эффективность. В частности, аппроксимированное направление Ньютона Гаусса, т.е. решение s к
| (6) |
(где J является якобианом F (x)), используется, чтобы помочь задать двумерное подпространство S. Вторые производные функционального fi компонента (x) не используются.
В каждой итерации метод предобусловленных методов сопряженных градиентов используется, чтобы приблизительно решить нормальные уравнения, т.е.
несмотря на то, что нормальные уравнения явным образом не формируются.
В этом случае функциональный f (x), который будет решен,
возможно подвергните линейным ограничениям. Алгоритм генерирует строго выполнимый, выполняет итерации схождения, в пределе, к локальному решению. Каждая итерация включает приближенное решение большой линейной системы (порядка n, где n является длиной x). Матрицы итерации имеют структуру матричного C. В частности, метод предобусловленных методов сопряженных градиентов используется, чтобы приблизительно решить нормальные уравнения, т.е.
несмотря на то, что нормальные уравнения явным образом не формируются.
Метод доверительной области подпространства используется, чтобы определить поисковое направление. Однако вместо того, чтобы ограничить шаг (возможно) одним отражательным шагом, как в нелинейном случае минимизации, кусочный отражающий поиск строки проводится в каждой итерации, как в квадратичном случае. См. [45] для деталей поиска строки. В конечном счете линейные системы представляют подход Ньютона, получая условия оптимальности первого порядка в решении, приводя к сильным локальным уровням сходимости.
Якобиан Умножает Функцию. lsqlin может решить проблему линейно-метода-наименьших-квадратов-с-ограничениями, не используя матричный C явным образом. Вместо этого это использует якобиан, умножают функциональный jmfun,
W = jmfun(Jinfo,Y,flag)
то, что вы обеспечиваете. Функция должна вычислить следующие продукты для матричного Y:
Если flag == 0 затем W = C'*(C*Y).
Если flag > 0 затем W = C*Y.
Если flag < 0 затем W = C'*Y.
Это может быть полезно, если C является большим, но содержит достаточно структуры, что можно записать jmfun, не формируя C явным образом. Для примера смотрите, что якобиан Умножает Функцию с Линейным методом наименьших квадратов.
Алгоритм 'interior-point' lsqlin использует выпуклый внутренней точкой quadprog Алгоритм. quadprog проблемное определение должно минимизировать квадратичную функцию
подвергните линейным ограничениям и связанным ограничениям. Функция lsqlin минимизирует квадратичную норму векторного Cx – d, подвергающегося линейным ограничениям и связанным ограничениям. Другими словами, lsqlin минимизирует
Это помещается в среду quadprog путем установки матрицы H на 2CTC и вектора c к (–2CTd). (Вектор свободных членов dTd не имеет никакого эффекта на местоположение минимума.) После этой переформулировки проблемы lsqlin алгоритм 'interior-point-convex' quadprog вычисляет решение.
Алгоритм 'interior-point-convex' quadprog имеет два пути выполнения кода. Это берет тот, когда матрица Гессиана, из которой H является обычной (полной) матрицей, удваивается, и это берет другой, когда H является разреженной матрицей. Для получения дополнительной информации разреженного типа данных, смотрите Разреженные матрицы (MATLAB). Обычно алгоритм быстрее для больших проблем, которые имеют относительно немного ненулевых условий, когда вы задаете H как sparse. Точно так же алгоритм быстрее для небольших или относительно плотных проблем, когда вы задаете H как full.
В задаче наименьших квадратов функциональный f (x) минимизирован, который сумма квадратов.
| (7) |
Проблемы этого типа происходят в большом количестве практических применений, особенно когда подходящие образцовые функции к данным, т.е. нелинейная оценка параметра. Они также распространены в управлении, где вы хотите вывод, y (x,t), чтобы следовать за некоторой непрерывной образцовой траекторией, φ (t), для векторного x и скалярного t. Эта проблема может быть выражена как
| (8) |
где y (x,t) и φ (t) является скалярными функциями.
Когда интеграл дискретизируется с помощью подходящей формулы квадратуры, вышеупомянутое может быть сформулировано как задача наименьших квадратов:
| (9) |
где и включайте веса квадратурной схемы. Обратите внимание на то, что в этой проблеме векторный F (x)
В проблемах этого вида невязка ∥F (x) ∥, вероятно, будет маленькой в оптимуме, поскольку это - общая практика, чтобы установить реалистично достижимые целевые траектории. Несмотря на то, что функция в LS может быть минимизирована с помощью общего метода безусловной минимизации, как описано в Основах Неограниченной Оптимизации, определенные характеристики проблемы могут часто использоваться, чтобы повысить итеративную эффективность процедуры решения. Градиент и матрица Гессиана LS имеют специальную структуру.
Обозначая m-by-n якобиевская матрица F (x) как J (x), вектор градиента f (x) как G (x), матрица Гессиана f (x) как H (x) и матрица Гессиана каждого Fi (x) как Hi (x), вы имеете
| (10) |
где
Матричный Q (x) имеет свойство, что, когда невязка ∥F (x) ∥ имеет тенденцию обнулять, когда xk приближается к решению, затем Q (x) также имеет тенденцию обнулять. Таким образом, когда ∥F (x) ∥ является маленьким в решении, очень эффективный метод состоит в том, чтобы использовать направление Ньютона Гаусса в качестве основания для процедуры оптимизации.
В методе Ньютона Гаусса поисковое направление, dk, получено в каждой главной итерации, k, который является решением проблемы линейного метода наименьших квадратов:
| (11) |
Направление, выведенное из этого метода, эквивалентно направлению Ньютона, когда условия Q (x) могут быть проигнорированы. Поисковый dk направления может использоваться в качестве части стратегии поиска строки гарантировать, что в каждой итерации функциональный f (x) уменьшается.
Метод Ньютона Гаусса часто сталкивается с проблемами, когда термин второго порядка Q (x) является значительным. Метод, который преодолевает эту проблему, является методом Levenberg-Marquardt.
Levenberg-Marquardt [25], и [27] метод использует поисковое направление, которое является решением линейной системы уравнений
| (12) |
или, опционально, уравнений
| (13) |
где скалярный λk управляет и значением и направлением dk. Установите опцию ScaleProblem на 'none' выбирать Equation 12 и устанавливать ScaleProblem на 'Jacobian' выбирать Equation 13.
Вы устанавливаете начальное значение параметра λ 0 использований опции InitDamping. Иногда, значение по умолчанию 0.01 этой опции может быть неподходящим. Если вы находите, что алгоритм Levenberg-Marquardt делает мало начальных успехов, попробуйте установку InitDamping к различному значению, чем значение по умолчанию, возможно, 1e2.
Когда λk является нулем, направление, dk идентичен тому из метода Ньютона Гаусса. Когда λk склоняется к бесконечности, dk склоняется к направлению быстрейшего спуска со значением, имеющим тенденцию обнулять. Это подразумевает, что для некоторого достаточно большого λk, термин F (xk + dk) < F (xk) сохраняется. Термином λk можно поэтому управлять, чтобы гарантировать спуск, даже когда с условиями второго порядка, которые ограничивают эффективность метода Ньютона Гаусса, сталкиваются. То, когда шаг успешен (дает более низкое значение функции), алгоритм устанавливает λ k +1 = λk/10. Когда шаг неудачен, алгоритм устанавливает λ k +1 = λk *10.
Внутренне, алгоритм Levenberg-Marquardt использует допуск оптимальности (останавливающий критерий) времен 1e-4 функциональный допуск.
Метод Levenberg-Marquardt поэтому использует поисковое направление, которое является пересечением направления Ньютона Гаусса и направления быстрейшего спуска. Это проиллюстрировано в рисунке 12-1, Методе Levenberg-Marquardt на Функции Розенброка. Решение для функции Розенброка сходится после 90 функциональных оценок по сравнению с 48 для метода Ньютона Гаусса. Более плохая эффективность частично, потому что метод Ньютона Гаусса является обычно более эффективным, когда невязка является нулем в решении. Однако такая информация не всегда доступна заранее, и увеличенная робастность метода Levenberg-Marquardt компенсирует свою случайную более плохую эффективность.
Рисунок 12-1, метод Levenberg-Marquardt на функции Розенброка
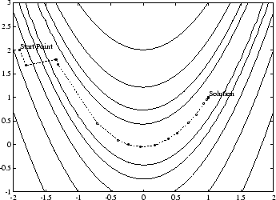
Для большего количества полного описания этой фигуры, включая скрипты, которые генерируют итеративные точки, смотрите Банановую Минимизацию Функции.