Этот пример показывает, как использовать приложение Оптимизации с решателем fmincon, чтобы минимизировать квадратичный предмет к линейным и нелинейным ограничениям и границам.
Приложение Оптимизации предупреждает, что будет удалено в будущем релизе.
Считайте проблему нахождения [x 1, x 2], который решает
подвергните ограничениям
Стартовым предположением для этой проблемы является x 1 = 3 и x 2 = 1.
function f = objecfun(x) f = x(1)^2 + x(2)^2;
function [c,ceq] = nonlconstr(x)
c = [-x(1)^2 - x(2)^2 + 1;
-9*x(1)^2 - x(2)^2 + 9;
-x(1)^2 + x(2);
-x(2)^2 + x(1)];
ceq = [];Введите optimtool в Командном окне, чтобы открыть приложение Оптимизации.
Выберите fmincon из выбора решателей и измените поле Algorithm на Active set.

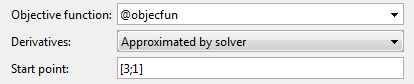
Введите @objecfun в поле Objective function, чтобы вызвать файл objecfun.m.
Введите [3;1] в поле Start point.
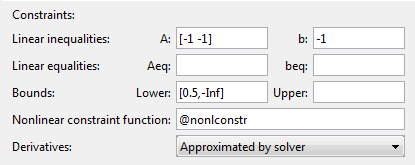
Задайте ограничения.
Установите связанный 0.5 ≤ x 1 путем ввода [0.5,-Inf] в поле Lower. Запись -Inf означает, что нет никакой нижней границы на x 2.
Установите линейное ограничение неравенства путем ввода [-1 -1] в поле A и введите -1 в поле b.
Установите нелинейные ограничения путем ввода @nonlconstr в поле Nonlinear constraint function.
В панели Options расширьте опцию Display to command window при необходимости и выберите Iterative, чтобы показать информацию об алгоритме в Командном окне для каждой итерации.

Нажмите кнопку Start как показано в следующей фигуре.
Когда алгоритм останавливается под Run solver and view results, следующая информация отображена:
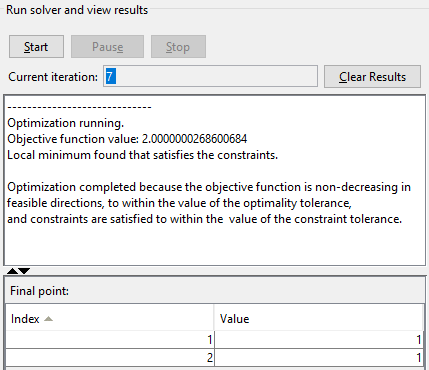
Значение Current iteration, когда отключенный алгоритм, который для этого примера является 7.
Окончательное значение целевой функции, когда отключенный алгоритм:
Objective function value: 2.0000000268595803
Сообщение завершения алгоритма:
Local minimum found that satisfies the constraints. Optimization completed because the objective function is non-decreasing in feasible directions, to within the value of the optimality tolerance, and constraints are satisfied to within the value of the constraint tolerance.
Конечный пункт, который для этого примера является
1
1 В Командном окне информация об алгоритме отображена для каждой итерации:
Max Line search Directional First-order
Iter F-count f(x) constraint steplength derivative optimality Procedure
0 3 10 2 Infeasible start point
1 6 4.84298 -0.1322 1 -5.22 1.74
2 9 4.0251 -0.01168 1 -4.39 4.08 Hessian modified twice
3 12 2.42704 -0.03214 1 -3.85 1.09
4 15 2.03615 -0.004728 1 -3.04 0.995 Hessian modified twice
5 18 2.00033 -5.596e-05 1 -2.82 0.0664 Hessian modified twice
6 21 2 -5.326e-09 1 -2.81 0.000522 Hessian modified twice
Active inequalities (to within options.ConstraintTolerance = 1e-06):
lower upper ineqlin ineqnonlin
3
4
Local minimum found that satisfies the constraints.
Optimization completed because the objective function is non-decreasing in
feasible directions, to within the value of the optimality tolerance,
and constraints are satisfied to within the value of the constraint tolerance.