Коэффициенты для систем УЧП в приложении PDE Modeler

Можно ввести коэффициенты для системы с N = уравнения 2 в приложении PDE Modeler. Для этого откройте приложение PDE Modeler и выберите Generic System.

Затем выберите PDE > PDE Specification.

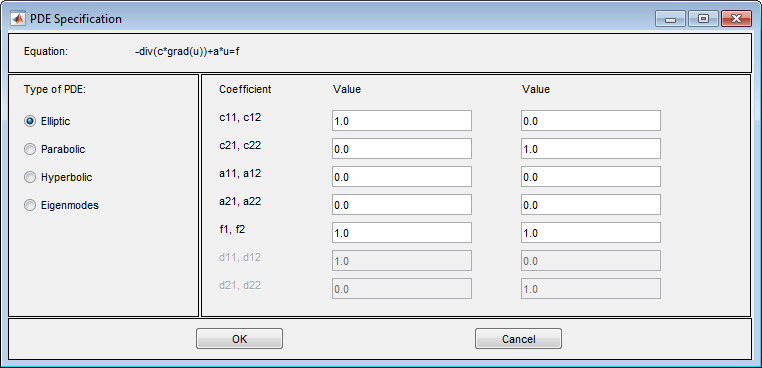
Введите символьные выражения для коэффициентов с помощью формы в Коэффициентах для Скалярных УЧП в Приложении PDE Modeler с дополнительными опциями для нелинейных уравнений. Дополнительные опции:

Представляйте i th компонент решения u с помощью 'u(i)' для i = 1 или 2.
Точно так же представляйте i th компоненты градиентов решения u с помощью 'ux(i)' и 'uy(i)' для i = 1 или 2.

Примечание

Для эллиптических проблем, когда вы включаете коэффициенты u(i), ux(i) или uy(i), необходимо использовать нелинейный решатель. Выберите Solve > Parameters > Use nonlinear solver.

Не используйте кавычки или ненужные пробелы в ваших записях.

Для более многомерных систем не используйте приложение PDE Modeler. Представляйте свои проблемные коэффициенты в командной строке.

Можно ввести скаляры в матрицу c, соответствуя этим уравнениям:

$\begin{matrix} - \nabla \cdot (c_{11} \nabla u_{1}) - \nabla \cdot (c_{12} \nabla u_{2}) + a_{11} u_{1} + a_{12} u_{2} = f_{1} \\ - \nabla \cdot (c_{21} \nabla u_{1}) - \nabla \cdot (c_{22} \nabla u_{2}) + a_{21} u_{1} + a_{22} u_{2} = f_{2} \end{matrix}$

Если вам нужны матричные версии какого-либо из коэффициентов cij, введите выражения, разделенные пробелами. Можно дать 1-, 2-, 3-, или матричные выражения с 4 элементами. Они означают:

Выражение с 1 элементом: $(\begin{matrix} c \\ 00 & c \end{matrix})$
Выражение с 2 элементами: $(\begin{matrix} c (1) \\ 00 & c (2) \end{matrix})$
Выражение с 3 элементами: $(\begin{matrix} c (1) & c (2) \\ c (2) & c (3) \end{matrix})$
Выражение с 4 элементами: $(\begin{matrix} c (1) & c (3) \\ c (2) & c (4) \end{matrix})$

Например, эти выражения показывают один из каждого типа (1-, 2-, 3-, и выражения с 4 элементами)

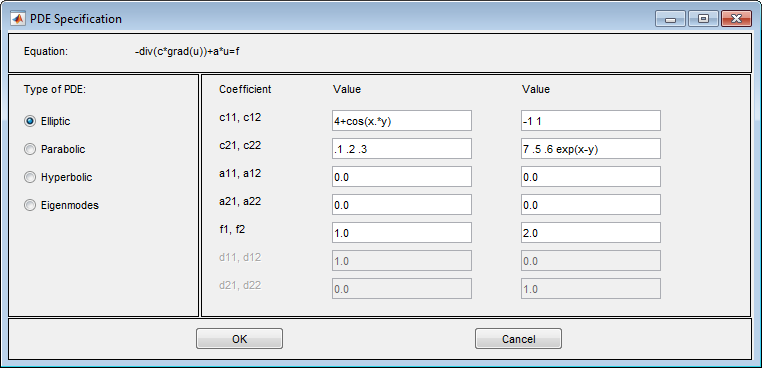
Эти выражения соответствуют уравнениям

$\begin{matrix} - \nabla \cdot ((\begin{matrix} 4 + потому что (x y) \\ 00 & 4 + потому что (x y) \end{matrix}) \nabla u_{1}) - \nabla \cdot ((\begin{matrix} - 1 \\ 001 \end{matrix}) \nabla u_{2}) = 1 \\ - \nabla \cdot ((\begin{matrix} .1 & .2 \\ .2 & .3 \end{matrix}) \nabla u_{1}) - \nabla \cdot ((\begin{matrix} 7 & .6 \\ .5 & \exp (x - y) \end{matrix}) \nabla u_{2}) = 2 \end{matrix}$

Документация Partial Differential Equation Toolbox

Поддержка

Памятка переводчика

1. Если смысл перевода понятен, то лучше оставьте как есть и не придирайтесь к словам, синонимам и тому подобному. О вкусах не спорим.

2. Не дополняйте перевод комментариями “от себя”. В исправлении не должно появляться дополнительных смыслов и комментариев, отсутствующих в оригинале. Такие правки не получится интегрировать в алгоритме автоматического перевода.

3. Сохраняйте структуру оригинального текста - например, не разбивайте одно предложение на два.

4. Не имеет смысла однотипное исправление перевода какого-то термина во всех предложениях. Исправляйте только в одном месте. Когда Вашу правку одобрят, это исправление будет алгоритмически распространено и на другие части документации.

5. По иным вопросам, например если надо исправить заблокированное для перевода слово, обратитесь к редакторам через форму технической поддержки.