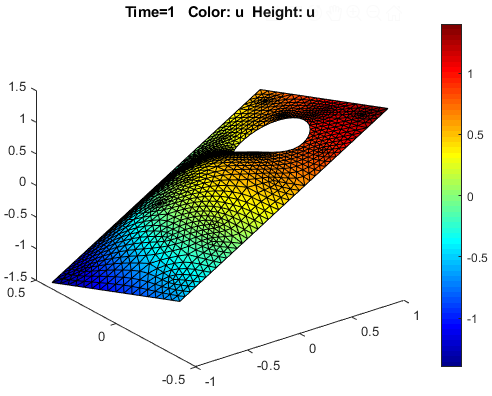
Этот пример показывает, как ввести время - и координатно-зависимые коэффициенты в приложении PDE Modeler.
Решите параболический УЧП,
со следующими коэффициентами:
d = 5
a = 0
f является линейным подъемом до 10, содержит в 10, затем сползает, отступают к 0:
c = 1 +.x2 + y 2
Чтобы решить это уравнение в приложении PDE Modeler, выполните эти шаги:
Запишите файл framp.m и сохраните его на своем пути MATLAB®.
function f = framp(t) if t <= 0.1 f = 10*t; elseif t <= 0.9 f = 1; else f = 10-10*t; end f = 10*f;
Откройте приложение PDE Modeler при помощи команды pdeModeler.
Отобразите линии сетки путем выбора Options> Grid.
Выровняйте новые формы к линиям сетки путем выбора Options> Snap.
Чертите прямоугольник с углами в (-1,-0.4), (-1 0.4), (1 0.4), и (1,-0.4). Для этого сначала нажмите![]() кнопку. Затем кликните по одному из углов с помощью левой кнопки мыши и перетащите, чтобы чертить прямоугольник.
кнопку. Затем кликните по одному из углов с помощью левой кнопки мыши и перетащите, чтобы чертить прямоугольник.
Нарисуйте круг с радиусом 0.2 и центр в (0.5,0). Для этого сначала нажмите![]() кнопку. Затем щелкните правой кнопкой по источнику и перетащите, чтобы нарисовать круг. Щелчок правой кнопкой ограничивает форму, которую вы чертите так, чтобы это был круг, а не эллипс. Если круг не является совершенным модульным кругом, дважды кликните его. В получившемся диалоговом окне задайте точное центральное местоположение и радиус круга.
кнопку. Затем щелкните правой кнопкой по источнику и перетащите, чтобы нарисовать круг. Щелчок правой кнопкой ограничивает форму, которую вы чертите так, чтобы это был круг, а не эллипс. Если круг не является совершенным модульным кругом, дважды кликните его. В получившемся диалоговом окне задайте точное центральное местоположение и радиус круга.
Смоделируйте геометрию путем ввода R1-C1 в поле Set formula.
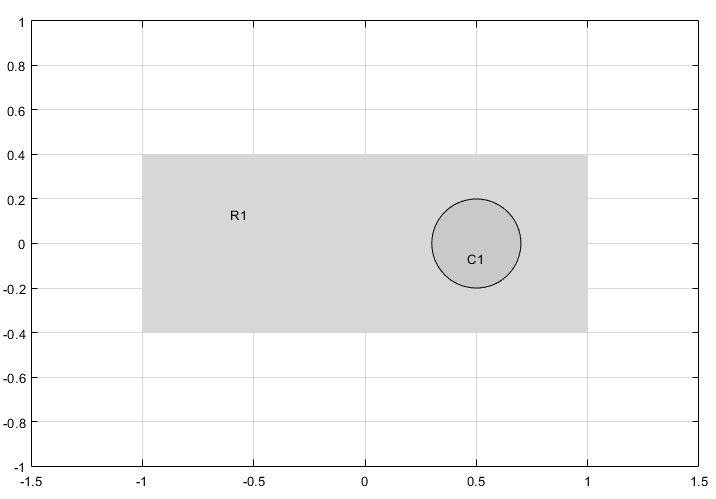
Проверяйте, что режим приложения установлен в Generic Scalar.
Задайте граничные условия. Для этого переключитесь на граничный режим путем выбора Boundary> Boundary Mode. Используйте Shift +click, чтобы выбрать несколько контуров. Затем выберите Boundary> Specify Boundary Conditions.
Для прямоугольника используйте граничное условие Дирихле с h = 1 и r = t*(x-y).
Для круга используйте Нейманово граничное условие с g = x.^2+y.^2 и q = 1.
Задайте коэффициенты путем выбора PDE> PDE Specification или нажатия кнопки PDE на панели инструментов. Выберите тип Parabolic УЧП. Задайте c = 1+x.^2+y.^2, a = 0, f = framp(t) и d = 5.
Не включайте кавычки или пробелы, когда вы зададите свои коэффициенты приложение PDE Modeler. Синтаксический анализатор интерпретирует все входные параметры как векторы символов. Это может неправильно истолковать пробел как векторный разделитель, как тогда, когда вектор MATLAB использует пространство, чтобы разделить элементы вектора.
Инициализируйте mesh путем выбора Mesh> Initialize Mesh.
Совершенствуйте mesh дважды путем выбора Mesh> Refine Mesh.
Улучшите треугольное качество путем выбора Mesh> Jiggle Mesh.
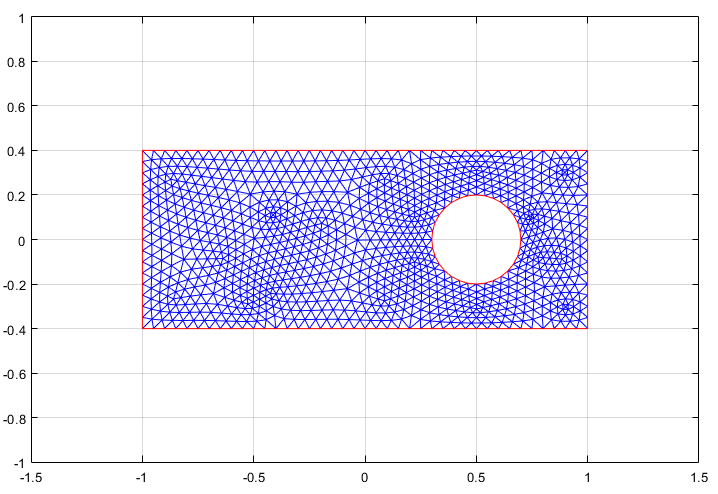
Установите начальное значение и время решения. Для этого выберите Solve> Parameters.
В получившемся диалоговом окне, набор время к linspace(0,1,50) и начальному значению u (t 0) к 0.
Решите уравнение путем выбора Solve> Solve PDE или нажатия кнопки = на панели инструментов.
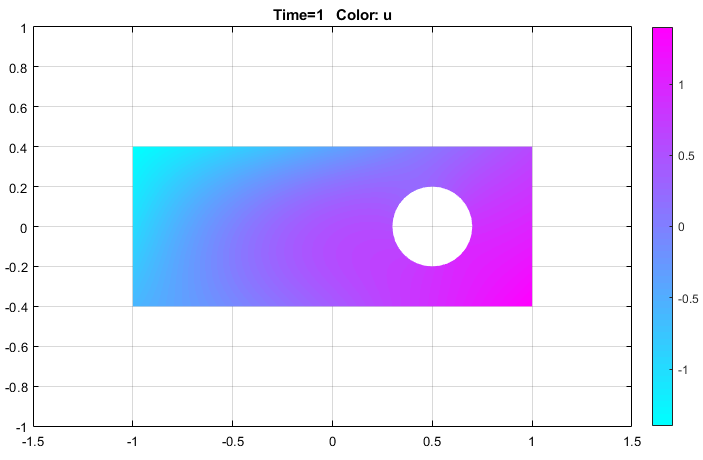
Визуализируйте решение как 3-D статический график. Для этого:
Выберите Plot> Parameters.
В получившемся диалоговом окне выберите опции Height (3-D plot) и Color.
Выберите опцию Show mesh.
Измените палитру на jet при помощи соответствующего выпадающего меню в том же диалоговом окне.