Partial Differential Equation Toolbox™ использует сетки с треугольными элементами для 2D конфигураций и сетки с четырехгранными элементами для 3-D конфигураций. Более ранние версии Partial Differential Equation Toolbox используют сетки в форме [p,e,t] трижды. Матрицы p, e и t представляют точки (узлы), элементы, и треугольники или тетраэдры mesh, соответственно. Более поздние версии тулбокса поддерживают сетки [p,e,t] по причинам совместимости.
Новые возможности не могут быть совместимы с устаревшим рабочим процессом. Для описания данных о mesh в рекомендуемом рабочем процессе смотрите Данные о Mesh.
Данные о mesh для 2D mesh имеют эти компоненты:
p (точки, узлы mesh) является 2-by-Np матрица узлов, где Np является количеством узлов в mesh. Каждый столбец p(:,k) состоит из x - координаты точки k в p(1,k) и y - координата точки k в p(2,k).
e (ребра) является 7-by-Ne матрица ребер, где Ne является количеством ребер в mesh. Ребра mesh в e и ребра геометрии имеют взаимно-однозначное соответствие. Матрица e представляет дискретные ребра геометрии таким же образом, как матрица t представляет дискретные поверхности. Каждый столбец в матрице e представляет одно ребро.
e(1,k) является индексом первой точки в ребре mesh k.
e(2,k) является индексом второй точки в ребре mesh k.
e(3,k) является значением параметров в первой точке ребра k. Значение параметров связано с длиной дуги вдоль геометрического ребра.
e(4,k) является значением параметров во второй точке ребра k.
e(5,k) является ID геометрического ребра, содержащего ребро mesh. Вы видите идентификаторы ребра при помощи команды pdegplot(geom,'EdgeLabels','on').
e(6,k) является номером субдомена на левой стороне ребра. Направление вдоль ребра дано путем увеличения значений параметров. Субдомен 0 является внешним видом геометрии.
e(7,k) является номером субдомена на правой стороне ребра.
t (треугольники) является 4-by-Nt матрица треугольников или 7-by-Nt матрица треугольников, в зависимости от того, вызываете ли вы generateMesh с набором пары "имя-значение" GeometricOrder к 'quadratic' или 'linear', соответственно. initmesh создает только элементы 'linear', которые имеют размер 4-by-Nt. Nt является количеством треугольников в mesh. Каждый столбец t содержит индексы точек в p, которые формируют треугольник. Исключением является последняя запись в столбце, который является номером субдомена. Треугольные точки упорядочены как показано.
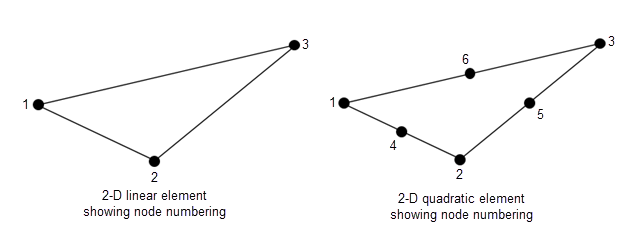
Данные о mesh для 3-D mesh имеют эти компоненты:
p (точки, узлы mesh) является 3-by-Np матрица узлов, где Np является количеством узлов в mesh. Каждый столбец p(:,k) состоит из x - координаты точки k в p(1,k), y - координате точки k в p(2,k) и z - координата точки k в p(3,k).
e является объектом, который сопоставляет поверхности mesh с контурами геометрии. Функции Partial Differential Equation Toolbox используют эту ассоциацию при преобразовании граничных условий, которые вы устанавливаете на контурах геометрии к поверхностям контура mesh.
t (тетраэдры) является или 11 Nt матрицей тетраэдров или 5 Nt матрицей тетраэдров, в зависимости от того, вызываете ли вы generateMesh с набором пары "имя-значение" GeometricOrder к 'quadratic' или 'linear', соответственно. Nt является количеством тетраэдров в mesh. Каждый столбец t содержит индексы точек в p, которые формируют четырехгранник. Исключением является последний элемент в столбце, который является номером субдомена. Точки четырехгранника упорядочены как показано.
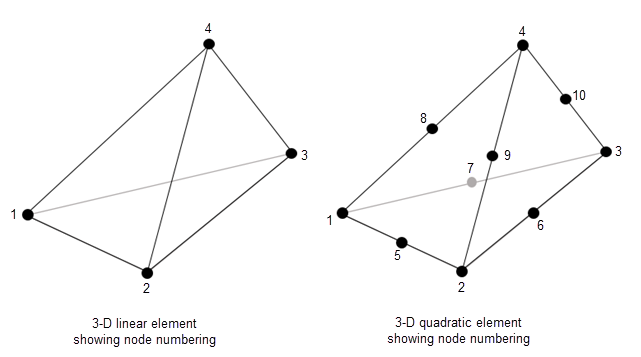
Можно создать mesh [p,e,t] при помощи одного из этих подходов:
Используйте функцию initmesh, чтобы создать 2D mesh [p,e,t].
Используйте функцию generateMesh, чтобы создать 2D или 3-D mesh как объект FEMesh. Затем используйте функцию meshToPet, чтобы преобразовать mesh в mesh [p,e,t].