Моделируйте полученный сигнал в сенсорной матрице
x = sensorsig(pos,ns,ang)x = sensorsig(pos,ns,ang,ncov)x = sensorsig(pos,ns,ang,ncov,scov)x = sensorsig(pos,ns,ang,ncov,scov,'Taper',taper)[x,rt] =
sensorsig(___)[x,rt,r]
= sensorsig(___)x = sensorsig(pos,ns,ang)pos представляет положения элементов массива, каждый из которых принят, чтобы быть изотропным. ns указывает на количество снимков состояния моделируемого сигнала. ang представляет входящие направления каждого сигнала плоской волны. Сигналы плоской волны приняты, чтобы быть сигналами постоянного модуля со случайными фазами.
Моделируйте полученный сигнал в массиве и используйте данные, чтобы оценить направления прибытия.
Примечание: Этот пример запускается только в R2016b или позже. Если вы используете более ранний релиз, заменяете каждый вызов функции с эквивалентным синтаксисом step. Например, замените myObject(x) на step(myObject,x).
Создайте универсальную линейную матрицу с 8 элементами, элементы которой расположены половина длины волны с интервалами независимо.
fc = 3e8; c = 3e8; lambda = c/fc; array = phased.ULA(8,lambda/2);
Моделируйте 100 снимков состояния полученного сигнала в массиве. Примите, что существует два сигнала, прибывающие из азимута 30 ° и 60 °, соответственно. Шум является белым через все элементы массива, и ОСШ составляет 10 дБ.
x = sensorsig(getElementPosition(array)/lambda,...
100,[30 60],db2pow(-10));Используйте beamscan пространственное средство оценки спектра, чтобы оценить направления прибытия, на основе моделируемых данных.
estimator = phased.BeamscanEstimator('SensorArray',array,... 'PropagationSpeed',c,'OperatingFrequency',fc,... 'DOAOutputPort',true,'NumSignals',2); [~,ang_est] = estimator(x);
Постройте пространственный спектр, следующий из процесса оценки.
plotSpectrum(estimator)

График показывает peaks на уровне 30 ° и 60 °.
Моделируйте получение двух некоррелированых входящих сигналов, которые имеют различные уровни мощности. Вектор под названием scov хранит уровни мощности.
Создайте универсальную линейную матрицу с 8 элементами, элементы которой расположены половина длины волны с интервалами независимо.
fc = 3e8; c = 3e8; lambda = c/fc; ha = phased.ULA(8,lambda/2);
Моделируйте 100 снимков состояния полученного сигнала в массиве. Примите, что один входящий сигнал происходит из 30 азимутов степеней и имеет силу 3 Вт. Второй входящий сигнал происходит из 60 азимутов степеней и имеет силу 1 Вт. Два сигнала не коррелируются друг с другом. Шум является белым через все элементы массива, и ОСШ составляет 10 дБ.
ang = [30 60];
scov = [3 1];
x = sensorsig(getElementPosition(ha)/lambda,...
100,ang,db2pow(-10),scov);Используйте beamscan пространственное средство оценки спектра, чтобы оценить направления прибытия, на основе моделируемых данных.
hdoa = phased.BeamscanEstimator('SensorArray',ha,... 'PropagationSpeed',c,'OperatingFrequency',fc,... 'DOAOutputPort',true,'NumSignals',2); [~,ang_est] = step(hdoa,x);
Постройте пространственный спектр, следующий из процесса оценки.
plotSpectrum(hdoa);

График показывает высокий пик в 30 градусах и более низкий пик в 60 градусах.
Моделируйте прием трех сигналов, два из которых коррелируются.
Создайте ковариационную матрицу сигнала, в которой первое и треть из трех сигналов коррелируются друг с другом.
scov = [1 0 0.6;... 0 2 0;... 0.6 0 1];
Моделируйте получение 100 снимков состояния трех входящих сигналов от 30 °, 40 °, и азимута на 60 °, соответственно. Массив, который получает сигналы, является универсальной линейной матрицей с 8 элементами, элементы которой являются распределенной половиной длины волны независимо. Шум является белым через все элементы массива, и ОСШ составляет 10 дБ.
pos = (0:7)*0.5; ns = 100; ang = [30 40 60]; ncov = db2pow(-10); x = sensorsig(pos,ns,ang,ncov,scov);
Моделируйте получение сигнала в URA. Сравните теоретическую ковариацию сигнала с ее выборочной ковариацией.
Создайте универсальную прямоугольную разрядку массивов 2 на 2 элементы 1/4-wavelength независимо.
pos = 0.25 * [0 0 0 0; -1 1 -1 1; -1 -1 1 1];
Задайте шумовую степень независимо для каждого из этих четырех элементов массива. Каждая запись в ncov является шумовой степенью элемента массива. Это положение элемента является соответствующим столбцом в pos. Примите, что шум является некоррелированым через элементы.
ncov = db2pow([-9 -10 -10 -11]);
Моделируйте 100 снимков состояния полученного сигнала в массиве и сохраните теоретические и эмпирические ковариационные матрицы. Примите, что один входящий сигнал происходит из азимута на 30 ° и повышения на 10 °. Второй входящий сигнал происходит из азимута на 50 ° и повышения на 0 °. Сигналы имеют силу 1 Вт и являются некоррелироваными.
ns = 100;
ang1 = [30; 10];
ang2 = [50; 0];
ang = [ang1, ang2];
rng default
[x,rt,r] = sensorsig(pos,ns,ang,ncov);Просмотрите значения теоретической ковариации и выборочной ковариации.
abs(rt)
ans = 4×4
2.1259 1.8181 1.9261 1.9754
1.8181 2.1000 1.5263 1.9261
1.9261 1.5263 2.1000 1.8181
1.9754 1.9261 1.8181 2.0794
abs(r)
ans = 4×4
2.2107 1.7961 2.0205 1.9813
1.7961 1.9858 1.5163 1.8384
2.0205 1.5163 2.1762 1.8072
1.9813 1.8384 1.8072 2.0000
Моделируйте получение сигнала в ULA, где шум между различными датчиками коррелируется.
Создайте универсальную линейную матрицу с 4 элементами, элементы которой являются распределенной половиной длины волны независимо.
pos = 0.5 * (0:3);
Задайте шумовую ковариационную матрицу. Значение в (k, _j _) положение в матрице ncov является ковариацией между k и j элементами массива, перечисленными в массиве.
ncov = 0.1 * [1 0.1 0 0; 0.1 1 0.1 0; 0 0.1 1 0.1; 0 0 0.1 1];
Моделируйте 100 снимков состояния полученного сигнала в массиве. Примите, что один входящий сигнал происходит из азимута на 60 °.
ns = 100; ang = 60; [x,rt,r] = sensorsig(pos,ns,ang,ncov);
Просмотрите теоретические матрицы и матрицы выборочной ковариации для полученного сигнала.
rt,r
rt = 4×4 complex
1.1000 + 0.0000i -0.9027 - 0.4086i 0.6661 + 0.7458i -0.3033 - 0.9529i
-0.9027 + 0.4086i 1.1000 + 0.0000i -0.9027 - 0.4086i 0.6661 + 0.7458i
0.6661 - 0.7458i -0.9027 + 0.4086i 1.1000 + 0.0000i -0.9027 - 0.4086i
-0.3033 + 0.9529i 0.6661 - 0.7458i -0.9027 + 0.4086i 1.1000 + 0.0000i
r = 4×4 complex
1.1059 + 0.0000i -0.8681 - 0.4116i 0.6550 + 0.7017i -0.3151 - 0.9363i
-0.8681 + 0.4116i 1.0037 + 0.0000i -0.8458 - 0.3456i 0.6578 + 0.6750i
0.6550 - 0.7017i -0.8458 + 0.3456i 1.0260 + 0.0000i -0.8775 - 0.3753i
-0.3151 + 0.9363i 0.6578 - 0.6750i -0.8775 + 0.3753i 1.0606 + 0.0000i
pos — Положения элементов в сенсорной матрицеПоложения элементов в сенсорной матрице, заданной как N-вектор-столбец или матрица. Значения в матрице находятся в модулях длины волны сигнала. Например, [0 1 2] описывает три элемента, которые расположены одна длина волны сигнала с интервалами независимо. N является числом элементов в массиве.
Размерности pos:
Для линейной матрицы вдоль оси y задайте y координаты элементов в векторе 1 на n.
Для плоского массива в yz плоскости задайте y и z координаты элементов в столбцах 2 N матрицей.
Для массива произвольной формы задайте x, y, и z координаты элементов в столбцах 3 N матрицей.
Типы данных: double
ns — Количество снимков состояния моделируемого сигналаКоличество снимков состояния моделируемого сигнала, заданного как положительный целочисленный скаляр. Функция возвращает это количество выборок на элемент массива.
Типы данных: double
ang — Направления входящих сигналов плоской волныНаправления входящих сигналов плоской волны, заданных как M-вектор-столбец или матрица в градусах. M является количеством входящих сигналов.
Размерности ang:
Если ang является 2 M матрицей, каждый столбец задает направление. Каждый столбец находится в форме [azimuth; elevation]. Угол азимута должен быть между –180 и 180 градусами, включительно. Угол повышения должен быть между –90 и 90 градусами, включительно.
Если ang является 1 M вектором, каждая запись задает угол азимута. В этом случае соответствующий угол повышения принят, чтобы быть 0.
Типы данных: double
ncov — Шумовые характеристикиШумовые характеристики, заданные как неотрицательный скаляр, вектор 1 на n положительных чисел или N на n положительная определенная матрица.
Размерности ncov:
Если ncov является скаляром, он представляет шумовую степень белого шума через все элементы датчика получения в ваттах. В частности, значение 0 указывает, что нет никакого шума.
Если ncov является вектором 1 на n, каждая запись представляет шумовую степень одного из элементов датчика в ваттах. Шум является некоррелированым через датчики.
Если ncov является N на n матрицей, он представляет ковариационную матрицу для шума через все элементы датчика.
Типы данных: double
scov — Характеристики входящего сигналаХарактеристики входящего сигнала, заданные как положительная скалярная величина, 1 M вектором положительных чисел или M-by-M положительной полуопределенной матрицей.
Размерности scov:
Если scov является скаляром, он представляет степень всех входящих сигналов в ваттах. В этом случае все входящие сигналы являются некоррелироваными и совместно используют тот же уровень мощности.
Если scov является 1 M вектором, каждая запись представляет степень одного из входящих сигналов в ваттах. В этом случае все входящие сигналы являются некоррелироваными друг с другом.
Если scov является M-by-M матрицей, он представляет ковариационную матрицу для всех входящих сигналов. Матрица описывает корреляцию среди входящих сигналов. В этом случае scov может быть действительным или комплексным.
Типы данных: double
taper — Заострение элемента массиваЗаострение элемента массива, заданное как скалярный или N с комплексным знаком-by-1 вектор-столбец. Размерность N является количеством элементов массива. Если taper является скаляром, все элементы в массиве используют то же значение. Если taper является вектором, каждая запись указывает, что заострение применилось к соответствующему элементу массива.
Типы данных: double
Поддержка комплексного числа: Да
x Полученный сигналns-by-N матрицаПолученный сигнал в сенсорной матрице, возвращенной как комплексный ns-by-N матрица. Каждый столбец представляет полученный сигнал в соответствующем элементе массива. Каждая строка представляет снимок состояния.
rt Теоретическая ковариационная матрицаТеоретическая ковариационная матрица полученного сигнала, возвращенного как комплексная N на n матрица.
r Матрица выборочной ковариацииМатрица выборочной ковариации полученного сигнала, возвращенного как комплексная N на n матрица. N является количеством элементов массива. Функция выводит эту матрицу от x.
Если вы задаете этот выходной аргумент, считаете создание ns больше, чем или равный N. В противном случае r имеет неполный ранг.
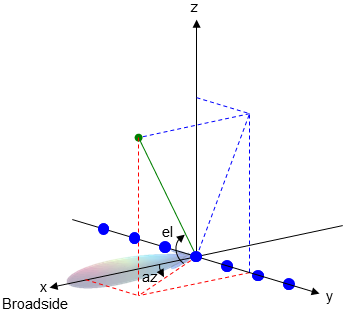
azimuth angle вектора является углом между x - ось и ортогональной проекцией вектора на плоскость xy. Угол положителен в движении от оси x к оси y. Углы азимута находятся между –180 и 180 градусами. elevation angle является углом между вектором и его ортогональной проекцией на xy - плоскость. Угол положителен при движении к положительному z - ось от плоскости xy. Эти определения принимают, что направлением опорного направления является положительный x - ось.
Угол повышения иногда задается в литературе как угол, который вектор делает с положительным z - ось. MATLAB® и продукты Phased Array System Toolbox™ не используют это определение.
Эта фигура иллюстрирует угол азимута и угол повышения для вектора, который появляется как зеленая сплошная линия. Система координат относительно центра универсальной линейной матрицы, элементы которой появляются как синие круги.
Указания и ограничения по применению:
Не поддерживает входные параметры переменного размера.
1. Если смысл перевода понятен, то лучше оставьте как есть и не придирайтесь к словам, синонимам и тому подобному. О вкусах не спорим.
2. Не дополняйте перевод комментариями “от себя”. В исправлении не должно появляться дополнительных смыслов и комментариев, отсутствующих в оригинале. Такие правки не получится интегрировать в алгоритме автоматического перевода.
3. Сохраняйте структуру оригинального текста - например, не разбивайте одно предложение на два.
4. Не имеет смысла однотипное исправление перевода какого-то термина во всех предложениях. Исправляйте только в одном месте. Когда Вашу правку одобрят, это исправление будет алгоритмически распространено и на другие части документации.
5. По иным вопросам, например если надо исправить заблокированное для перевода слово, обратитесь к редакторам через форму технической поддержки.