Канал распространения 2D луча является следующим, подходят в сложности от канала свободного пространства, и самый простой случай многопутевой среды распространения. Канал свободного пространства моделирует прямолинейный путь угла обзора от точки 1 до точки 2. В канале 2D луча носитель задан как гомогенный, изотропный носитель с отражающимся плоским контуром. Контур всегда устанавливается в z = 0. Существует самое большее два распространения лучей от точки 1 до точки 2. Первый путь к лучу распространяет вдоль того же пути угла обзора как в канале свободного пространства (см. Систему phased.FreeSpace object™). Путь угла обзора часто называется прямым путем. Второй луч отражается от контура прежде, чем распространить к точке 2. Согласно Закону Отражения, угол отражения равняется углу падения. В ближних симуляциях, таких как системы сотовой связи и автомобильные радары, можно принять, что отражающаяся поверхность, земля или океанская поверхность, является плоской.
phased.TwoRayChannel и задержка распространения модели Системных объектов phased.WidebandTwoRayChannel, сдвиг фазы, эффект Доплера и эффекты потерь для обоих путей. Для отраженного пути эффекты потерь включают отражательную потерю в контур.
Фигура иллюстрирует два пути к распространению. От исходного положения, ss, и положения получателя, sr, можно вычислить углы падения обоих путей, θ′los и θ′rp. Углы падения являются повышением и углами азимута прибывающего излучения относительно системы локальной координаты. В этом случае система локальной координаты совпадает с глобальной системой координат. Можно также вычислить углы передачи, θlos и θrp. В глобальных координатах угол отражения на контуре совпадает с углами θrp и θ′rp. Отражательный угол важен, чтобы знать, когда вы используете зависимые углом данные отражательной потери. Можно определить отражательный угол при помощи функции rangeangle и установки ссылочных осей к глобальной системе координат. Общую длину пути для пути угла обзора показывает в фигуре Rlos, который равен геометрическому расстоянию между источником и получателем. Общей длиной пути для отраженного пути является Rrp= R1 + R2. Количество L является наземной областью значений между источником и получателем.
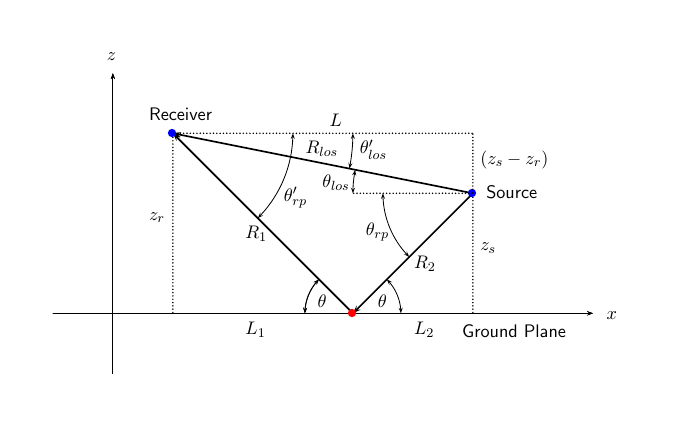
Можно легко вывести точные формулы для длин пути и углов с точки зрения наземной области значений и высот объектов в глобальной системе координат.