Для первого шага в режиме реального времени Образцовый Рабочий процесс Подготовки, вы получаете результаты симуляции переменного шага ссылочной версии вашей модели Simscape™. Ссылочные результаты обеспечивают базовую линию, против которой можно оценить точность модели, когда вы изменяете его. Этот пример показывает, как анализировать ссылочные результаты и размер шага, к которому берет решатель переменного шага:
Оцените максимальный размер шага, который можно использовать для симуляции фиксированного шага
Идентифицируйте события, которые имеют потенциал, чтобы ограничить максимальный размер шага
Разрывы и быстрые изменения требуют размеров небольшого шага для того, чтобы точно получить эти движущие силы. Максимальный размер шага, который можно использовать для симуляции фиксированного шага, должен быть достаточно небольшим, чтобы гарантировать точные результаты. Если ваша модель содержит такую динамику, то возможно, что необходимый размер шага для точных результатов, Tsmax, является слишком небольшим. Размер шага, который является слишком небольшим, не позволяет вашему компьютеру в реальном времени закончить вычислять решение для любого данного шага в симуляции.
Анализ в этом примере помогает вам оценить максимальный размер шага, что решатели фиксированного шага могут использовать и все еще получить точные результаты. Можно также использовать анализ, чтобы определить, какие элементы влияют на максимальный размер шага для точных результатов. Для получения дополнительной информации о том, как получение ссылочных результатов и выполнение анализа неродного размера помогают вам подготовить свою модель к симуляции в реальном времени, видеть Образцовые Цели Подготовки.
Открыть эталонную модель, в командной строке MATLAB®, введите:
model = 'ssc_pneumatic_rts_reference';
open_system(model)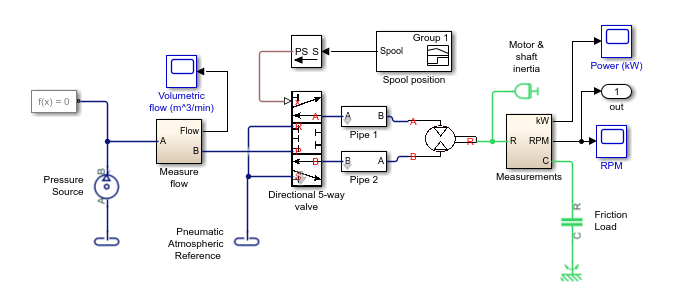
Моделируйте модель:
sim(model)
Создайте полулогарифмический график, который показывает, как размер шага для решателя отличается во время симуляции.
h1 = figure; semilogy(tout(1:end-1),diff(tout),'-x') title('Solver Step Size') xlabel('Time (s)') ylabel('Step Size (s)')
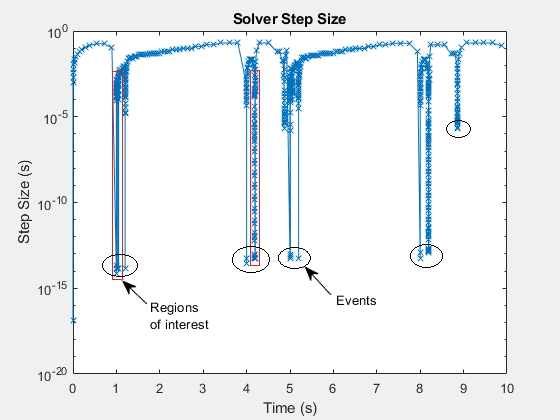
Для большой части симуляции размер шага больше, чем значение Tsmax в графике. Соответствующее значение, ~0.001 секунды, является предполагаемым максимальным размером шага для достижения точных результатов во время симуляции фиксированного шага с моделью. Чтобы видеть, как сконфигурировать размер шага для решателей фиксированного шага для симуляции в реальном времени, смотрите, Выбирают Step Size и Number of Iterations.
Маркеры x в графике указывают время, когда решатель взял, чтобы выполнить один шаг в тот момент в симуляции. Данные неродного размера дискретны. Строка, которая соединяет дискретные точки, существует только, чтобы помочь вам видеть порядок отдельных времен выполнения в течение симуляции.
Значительное сокращение в размере шага указывает, что решатель обнаруживает событие пересечения нулем. Обнаружение пересечения нулем может произойти, когда значение сигнала изменяет знак или пересекает порог. Симуляция уменьшает размер шага, чтобы получить динамику для события пересечения нулем точно. После того, как решатель обрабатывает динамику для события пересечения нулем, размер шага симуляции может увеличиться. Для решателя возможно сделать несколько небольших шагов прежде, чем возвратиться к размеру шага, который предшествует событию пересечения нулем. Области в красных полях содержат изменения во время восстановления для переменного решателя шага.
Чтобы видеть различные поведения постпересечения нулем, масштабируйте в область в красном поле во время (t) = ~1 секунда.
 Скрипт для того, чтобы увеличить масштаб
Скрипт для того, чтобы увеличить масштаб
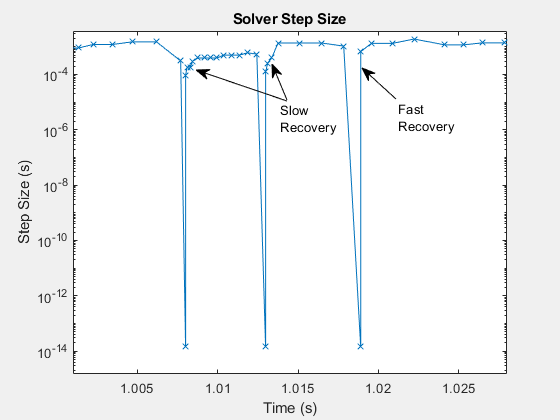
После t = 1,005 секунды, размер шага уменьшается с ~10e-3 секунд до меньше, чем 10e-13 секунд, чтобы получить событие. Размер шага увеличивается быстро до ~10e-5 секунд, и затем медленно к ~10e-4 секундам. Размер шага уменьшается, чтобы получить второе событие и восстанавливается быстро, и затем медленно к размеру шага до первого события. Низкие скорости восстановления указывают, что симуляция использует небольшие шаги, чтобы получить динамику элементов в вашей модели. Если необходимый размер шага ограничивает максимальный размер фиксированного шага достаточно маленьким значением, то переполнение может произойти, когда вы делаете попытку симуляции на своем компьютере в реальном времени.
Типы элементов, которые требуют размера небольшого шага:
Элементы, которые вызывают разрывы, такие как трение промаха палки и жесткие остановки
Элементы, которые имеют небольшие временные константы, такие как маленькие массы с незатухающими, жесткими пружинами и гидросхемы с маленькими, сжимаемыми объемами
Размер шага восстанавливается более быстро после того, как он замедляется, чтобы обработать событие, которое происходит перед t = 1,02 секунды. Это событие, менее вероятно, потребует, чтобы размеры небольшого шага достигли точных результатов.
Чтобы видеть различные типы медленных восстановлений решателя, масштабируйте в область в красном поле в t = ~4.2 секунды.
h1; xZoomStart2 = 4.16; xZoomEnd2 = 4.24; yZoomStart2 = 10e-20; yZoomEnd2 = 10e-1; axis([xZoomStart2 xZoomEnd2 yZoomStart2 yZoomEnd2]);
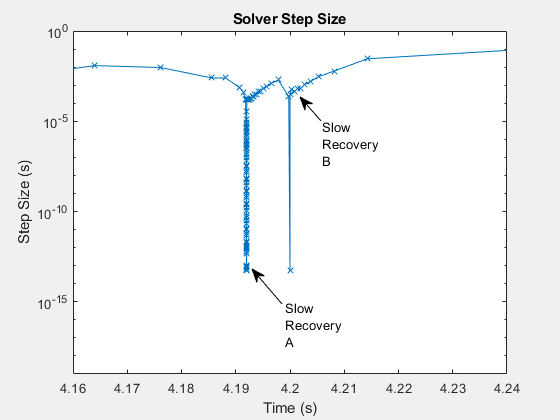
Так же, как существуют различные типы событий, которые заставляют решатели замедляться, существуют различные типы медленного восстановления решателя. События, которые происходят незадолго до t = 4,19 и 4,2 секунды оба, включают нулевые пересечения. Решатель берет серию прогрессивно больших шагов, когда он достигает размера шага до события. Большое количество очень небольших шагов, которые следуют за нулем, пересекающимся при Медленном Восстановлении A, указывает, что элемент, который вызвал нулевое пересечение, также численно жесток.
Более быстрое увеличение неродного размера после события, которое происходит в t = 4,2 секунды, указывает, что элемент, который вызвал нуль, пересекающийся перед Медленным Восстановлением B, не так жесток как событие при Медленном Восстановлении A.
Чтобы видеть результаты, откройте Проводник Результатов Simscape.
sscexplore(simlog)
Исследуйте угловую скорость. В окне Simscape Results Explorer, в симуляции регистрируют древовидную иерархию, выбирают Measurements> Ideal Rotational Motion Sensor> ![]() w.
w.
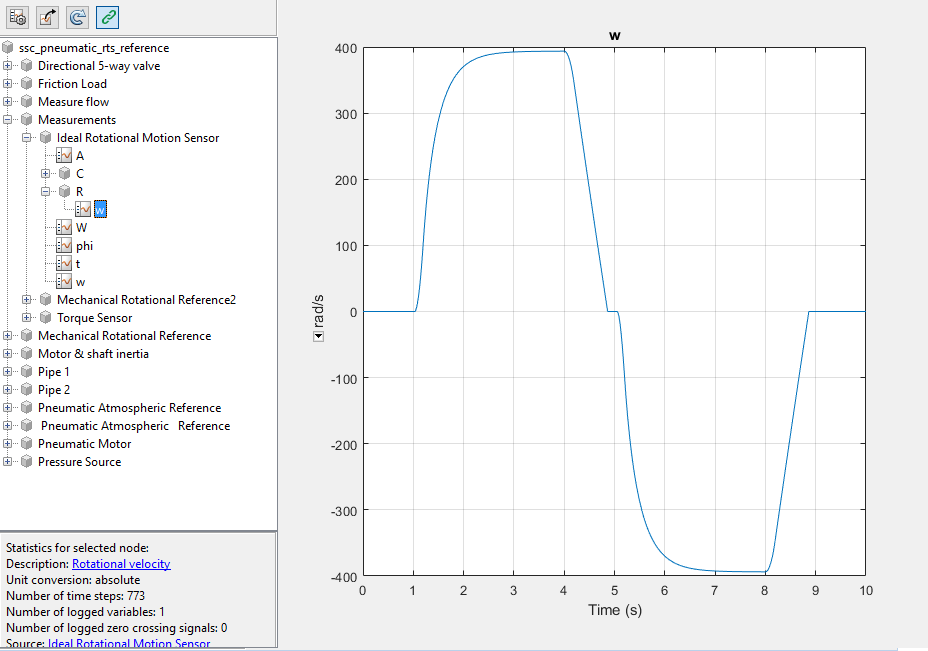
Чтобы добавить график потока газа, выберите Measure Flow> Pneumatic Mass & Heat Flow Sensor и затем, используйте Ctrl+click, чтобы выбрать ![]() G_ps.
G_ps.
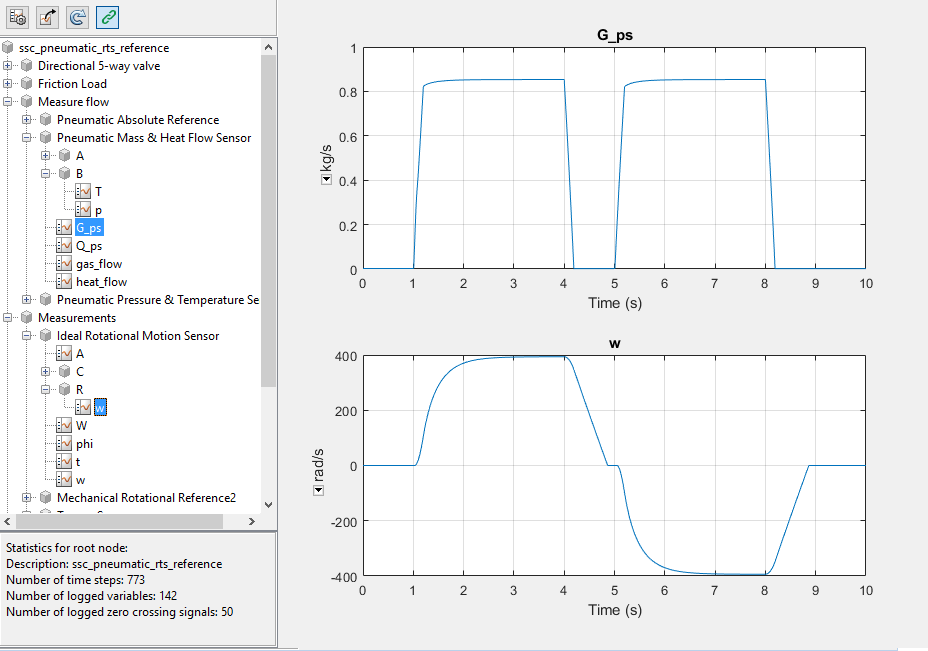
Медленные времена восстановления происходят, когда симуляция инициализирует, и приблизительно в t = 1, 4, 5, 8, и 9 секунд. Эти периоды небольших шагов совпадают с этими временами:
Частота вращения двигателя является близким нулевым об/мин (время симуляции t = ~ 1, 5, и 9 секунд)
Ступенчатое изменение в частоте вращения двигателя инициируется от установившейся скорости до новой скорости (время t = ~ 4 и 8 секунд)
Ступенчатое изменение в скорости потока жидкости инициируется от установившейся скорости до новой скорости потока жидкости (время t = ~ 4 и 8 секунд)
Объемный расход является близким нулем kg/s (t = ~ 1, 4, и 5 секунд),
Эти результаты показывают, что медленные восстановления неродного размера происходят, скорее всего, из-за элементов в модели, которые включают трение или которые имеют маленькие, сжимаемые объемы. Чтобы видеть, как идентифицировать проблематичные элементы и изменить их, чтобы увеличить скорость симуляции, смотрите, Уменьшают Числовую Жесткость и Уменьшают Нулевые Пересечения.