Субнормальные числа, раньше известные как нестандартные числа в литературе с плавающей точкой, заполняют разрыв потери значимости вокруг нуля в арифметике с плавающей точкой. Субнормальные значения являются специальной категорией значений с плавающей точкой, которые слишком близки к 0.0, который будет представлен как нормированное значение. Ведущая мантисса (мантисса) субнормального номера является нулем. При добавлении и вычитании чисел с плавающей запятой, субнормальные числа предотвращают потерю значимости.
Используя субнормальные числа обеспечивает точность вне нормального представления при помощи начальных нулей в мантиссе, чтобы представлять меньшие значения после того, как представление достигнет минимальной экспоненты. Когда значение приближается к 0.0, вы обмениваете точность на расширенную область значений. Субнормальные числа полезны, если ваше приложение требует дополнительной области значений.
Однако в системе реального времени, с помощью субнормальных чисел может существенно увеличить задержку выполнения, приводящую к чрезмерным полям проекта и переполнениям в реальном времени. Если симуляция или сгенерированный код выполняют вычисления, которые производят или используют субнормальные числа, выполнение этих вычислений может быть до 50 раз медленнее, чем подобные вычисления на нормальных числах. Фактическое время симуляции или выполнения кода для субнормальных вычислений номера зависит от вашей компьютерной операционной среды. Как правило, для настольных процессоров, время выполнения для субнормальных вычислений номера в пять раз медленнее, чем подобные вычисления на нормальных числах.
Минимизировать возможность выполнения замедляется или переполняется из-за субнормальной задержки вычисления номера, выполнить одно из следующих действий:
В вашей модели вручную сбросьте, чтобы обнулить любое поступление, или вычислил субнормальные значения во входных параметрах и ключевых операциях, таких как размытия и фильтры. Для примера смотрите Числа Поднормали Сброса, чтобы Обнулить.
Обнаружить субнормальное значение для одинарной точности, 32-битного числа с плавающей запятой:
Найдите самый маленький нормированный номер на хосте MATLAB®. В Командном окне введите:
>> SmallestNormalSingle = realmin('single')FLT_MIN, заданный в float.h, является эквивалентным to realmin('single').Ищите значения в области значений:
0 < fabsf(x) < SmallestNormalSingle
Обнаружить субнормальное значение для двойной точности, 64-битного числа с плавающей запятой:
Найдите самый маленький нормированный номер на хосте MATLAB. В Командном окне введите:
>> SmallestNormalDouble = realmin('double') DBL_MIN, заданный в float.h, является эквивалентным to realmin('double').Чтобы обнаружить субнормальное значение, ищите значения в этой области значений:
0 < fabs(x) < SmallestNormalDouble
На вашем процессоре режим сброса к нулю набора или, с вашим компилятором, задает опцию, чтобы отключить субнормальные числа. Режимы сброса к нулю обрабатывают субнормальный номер как 0, когда это - вход к операции с плавающей точкой. Потеряйте значимость исключения не происходят в режиме сброса к нулю.
Например, в процессорах Intel®, сброс к нулю (FTZ) и флаги denormals-are-zero (DAZ) в регистре MXCSR управляют вычислениями с плавающей точкой. Для gcc компилятора на Linux -ffast-math устанавливает резкую потерю значимости (FTZ), сброс к нулю, в то время как –O3 -ffast-math возвращается к постепенной потере значимости, с помощью субнормальных чисел.
Для получения дополнительной информации смотрите IEEE® Standard 754, Стандарт IEEE для Арифметики С плавающей точкой.
Эта модель показывает, как использование субнормальных чисел увеличивает время симуляции к ~5 разам.
Откройте модель ex_subnormal. Усиление установлено в субнормальное значение realmin('double')/2.
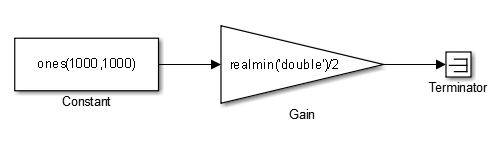
Запускать симуляцию, в Командном окне, for k=1:5, tic; sim('ex_subnormal'); toc,end типа. Наблюдайте прошедшие времена для симуляции с помощью поднормали, подобной следующему:
>> for k=1:5, tic; sim('ex_subnormal'); toc,end Elapsed time is 9.909326 seconds. Elapsed time is 9.617966 seconds. Elapsed time is 9.797183 seconds. Elapsed time is 9.702397 seconds. Elapsed time is 9.893946 seconds.
Установите Усиление на номер, 2, который не является субнормальным значением:
>> set_param('ex_subnormal/Gain', 'Gain', '2');
Запускать симуляцию, в Командном окне, for k=1:5, tic; sim('ex_subnormal'); toc,end типа. Наблюдайте прошедшие времена для симуляций, которые не используют субнормальные значения, подобные следующему:
>> for k=1:5, tic; sim('ex_subnormal'); toc,end Elapsed time is 2.045123 seconds. Elapsed time is 1.796598 seconds. Elapsed time is 1.758458 seconds. Elapsed time is 1.721721 seconds. Elapsed time is 1.780569 seconds.
Этот пример показывает, как сбросить числа поднормали одинарной точности, чтобы обнулить.
Откройте модель ex_flush_to_zero:
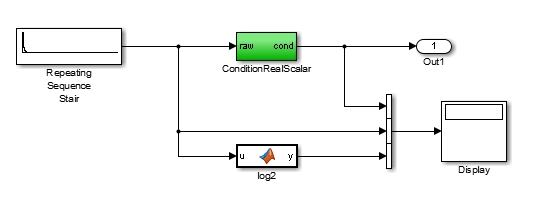
Repeating Sequence Stair генерирует последовательность чисел от двух возведенных в степень из 0 до двух возведенных в степень из-165. Последовательность приближается к нулю.
ConditionRealScalar сбрасывает субнормальные значения одинарной точности, которые являются меньше, чем realmin('single'), чтобы обнулить.
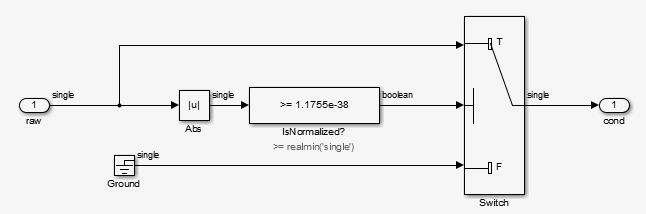
Блок MATLAB function log2 генерирует основу 2 логарифма Repeating Sequence Stair вывод. А именно, log2 генерирует числа 0 до-165.
На Simulation> панель Stepping Options:
Выберите Enable stepping back.
Выберите Pause simulation when time reaches и введите 121.
В окне модели запустите симуляцию. Симуляция делает паузу в T=121. Отображенные значения:
ConditionRealScalar вывод приближается к нулю.
Repeating Sequence Stair output приближается к нулю.
Шаг симуляция передает T=127. ConditionRealScalar сбрасывает субнормальное значение вывод от Repeating Sequence Stair, чтобы обнулить.
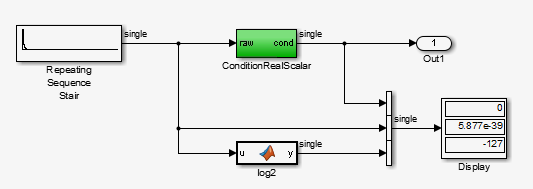
Продолжите продвигаться симуляция вперед. ConditionRealScalar сбрасывает субнормальные значения одинарной точности вывод от Repeating Sequence Stair, чтобы обнулить. Когда T=150, вывод Repeating Squence Stair является самостоятельно нулем.