Дискретное преобразование Фурье с алгоритмом Goertzel второго порядка
dft_data = goertzel(data)
dft_data = goertzel(data,freq_indices)
dft_data = goertzel(data,freq_indices,dim)
dft_data = goertzel(data) возвращает дискретное преобразование Фурье (DFT) входных данных, data, с помощью алгоритма Goertzel второго порядка. Если data является матрицей, goertzel вычисляет ДПФ каждого столбца отдельно. Можно задать типы данных как двойную или одинарную точность.
dft_data = goertzel(data,freq_indices) возвращает ДПФ для индексов частоты freq_indices. Значения freq_indices могут быть любым целым числом или частью.
dft_data = goertzel(data,freq_indices,dim) вычисляет ДПФ матричного data по измерению dim.
Оцените частоты тона, сгенерированного путем нажатия 1 кнопки на телефонной клавиатуре.
Номер 1 производит тон с частотами 697 и 1 209 Гц. Сгенерируйте 205 выборок тона с частотой дискретизации 8 кГц.
Fs = 8000; N = 205; lo = sin(2*pi*697*(0:N-1)/Fs); hi = sin(2*pi*1209*(0:N-1)/Fs); data = lo + hi;
Используйте алгоритм Goertzel, чтобы вычислить ДПФ тона. Выберите индексы, соответствующие частотам раньше, генерировали числа 0 до 9.
f = [697 770 852 941 1209 1336 1477]; freq_indices = round(f/Fs*N) + 1; dft_data = goertzel(data,freq_indices);
Постройте значение ДПФ.
stem(f,abs(dft_data)) ax = gca; ax.XTick = f; xlabel('Frequency (Hz)') title('DFT Magnitude')
Сгенерируйте шумный косинус с частотными составляющими на уровне 1,24 кГц, 1,26 кГц и 10 кГц. Задайте частоту дискретизации 32 кГц. Сбросьте генератор случайных чисел для восстанавливаемых результатов.
rng default Fs = 32e3; t = 0:1/Fs:2.96; x = cos(2*pi*t*10e3) + cos(2*pi*t*1.24e3) + cos(2*pi*t*1.26e3) ... + randn(size(t));
Сгенерируйте вектор частоты. Использование алгоритм Goertzel, чтобы вычислить ДПФ ограничивает область значений частот к между 1.2 и 1,3 кГц.
N = (length(x)+1)/2; f = (Fs/2)/N*(0:N-1); indxs = find(f>1.2e3 & f<1.3e3); X = goertzel(x,indxs);
Постройте среднеквадратический спектр, выраженный в децибелах.
plot(f(indxs)/1e3,mag2db(abs(X)/length(X))) title('Mean Squared Spectrum') xlabel('Frequency (kHz)') ylabel('Power (dB)') grid
Алгоритм Goertzel реализует ДПФ как рекурсивное разностное уравнение. Чтобы установить это разностное уравнение, выразите ДПФ как свертку N - вход точки, x (n), с импульсным ответом, где и u (n) является модульной последовательностью шага.
Z-преобразование импульсного ответа
Прямая форма II реализаций:
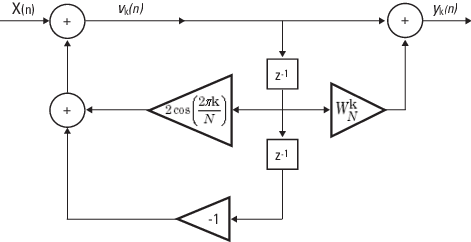
Можно также вычислить ДПФ с:
[1] Proakis, Джон Г. и Димитрис Г. Манолакис. Цифровая обработка сигналов: Принципы, Алгоритмы и Приложения. 3-й Выпуск. Верхний Сэддл-Ривер, NJ: Prentice Hall, 1996, стр 480–481.
[2] Burrus, К. Сидни и Томас В. Парки. DFT/FFT и Алгоритмы Свертки: Теория и Реализация. Нью-Йорк: John Wiley & Sons, 1985.
