Вы моделируете каждый компонент в структуре системы, чтобы представлять физическое или функциональное поведение того компонента. Вы проверяете основное поведение компонента путем симуляции их использующий тестовые данные.
Большая картина всей системы полезна при моделировании отдельных компонентов. Начните, загрузив образец модели:
open_system(fullfile(matlabroot,... 'help', 'toolbox', 'simulink', 'examples', 'system_layout'))
Simulink® модель компонента основана на нескольких отправных точках:
Явное математическое отношение между выводом и входом физического компонента — можно вычислить выходные параметры компонента от входных параметров, прямо или косвенно, посредством алгебраических вычислений и интегрирования дифференциальных уравнений. Например, вычисление уровня воды в корпусе, учитывая уровень притока является явным отношением. Каждый блок Simulink выполняется на основе определения вычислений от его входных параметров до его выходных параметров.
Неявное математическое отношение между образцовыми переменными физического компонента — поскольку переменные являются взаимозависимыми, присваивая вход и вывод к компоненту, не является прямым. Например, напряжение в + конец двигателя, соединенного в схеме и напряжении в – конец, имеет неявное отношение. Чтобы смоделировать такое отношение в Simulink, можно или использовать физические инструменты моделирования, такие как Simscape™ или смоделировать эти переменные как часть большего компонента, который позволяет определение ввода/вывода. Иногда, более близкий контроль моделирования целей и определений компонента помогает задать отношения ввода/вывода.
Данные получили из фактической системы — Вы измерили данные о вводе/выводе из фактического компонента, но полностью заданное математическое отношение не существует. Много устройств не смоделировали компоненты, которые соответствуют этому описанию. Примером было бы тепло, которое рассеивает телевизор. Можно использовать System Identification Toolbox™, чтобы задать отношение ввода/вывода для такой системы.
Явное функциональное определение — Вы задаете выходные параметры функционального компонента от входных параметров до алгебраических и логических вычислений. Переключающаяся логика термостата является примером. Можно смоделировать самые функциональные отношения как блоки Simulink и подсистемы.
Этот учебные модели физические и функциональные компоненты с явными отношениями ввода/вывода:
Используйте системные уравнения, чтобы создать модель Simulink.
Добавьте блоки Simulink в Редакторе Simulink. Блоки представляют коэффициенты и переменные из уравнений. Соедините блоки.
Создайте модель для каждого компонента отдельно. Самый эффективный способ создать модель системы состоит в том, чтобы рассмотреть компоненты независимо.
Начните построением простых моделей с помощью аппроксимации системы. Идентифицируйте предположения, которые могут влиять на точность вашей модели. Итеративно добавляйте деталь, пока уровень сложности не удовлетворит требования точности моделирования.
Опишите отношения между компонентами, например, данными, энергией и передачей силы. Используйте системные уравнения, чтобы создать графическую модель системы в Simulink.
Некоторые вопросы спросить, прежде чем вы начнете моделировать компонент:
Каковы константы для каждого компонента и значений, которые не изменяются, если вы не изменяете их?
Каковы переменные для каждого компонента и значения, которые изменяются во времени?
Сколько переменных состояния компонент имеет?
Выведите уравнения для каждого компонента используя научные принципы. Много системных уравнений попадают в три категории:
Для непрерывных систем дифференциальные уравнения описывают скорость изменения переменных с уравнениями, определенными для всех значений времени. Например, дифференциальное уравнение второго порядка дает скорость автомобиля:
Для дискретных систем разностные уравнения описывают скорость изменения переменных, но уравнения определены только в конкретные моменты времени. Например, следующее разностное уравнение дает управляющий сигнал от дискретного пропорционально-дифференциального регулятора:
Уравнения без производных являются алгебраическими уравнениями. Например, алгебраическое уравнение дает общий ток в параллельной схеме с двумя компонентами:
Колеса и Линейное Движение. Существует две силы, которые действуют на колесо:
Сила, прикладывавшая двигателем — Эта сила, F действует в направлении изменения скорости и является входом к подсистеме колеса.
Сила сопротивления — Эта сила Fdrag действует против направления изменения скорости и является функцией самой скорости:
Ускорение пропорционально сумме этих сил:
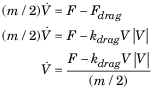
Где kdrag является коэффициентом сопротивления, и m является массой робота. Каждое колесо несет половину этой массы.
Создайте модель колеса:
В модели макета дважды кликните Правильную подсистему Колеса, чтобы отобразить пустую подсистему. Удалите связь между Inport и блоками Выходного порта.
Скорость модели и ускорение. Добавьте блок Integrator. Оставьте начальное условие как 0. Вывод этого блока является скоростью, V, и вход является ускорением, Vdot.
Смоделируйте силу сопротивления. Добавьте блок Fcn от библиотеки User-Defined Functions. Установите выражение на k_drag*u*abs(u). Можно изменить размер блока, чтобы видеть выражение на его значке. Блок Fcn обеспечивает быстрый способ ввести простые математические выражения одной входной переменной, u.
Вычтите силу сопротивления из моторной силы с блоком Subtract и завершите уравнение ускорения силы с блоком Gain с параметром 1/(2*m).
Чтобы инвертировать направление блока Fcn, щелкните правой кнопкой по блоку и выберите Rotate & Flip > Flip Block. Установите связи между блоками как показано.
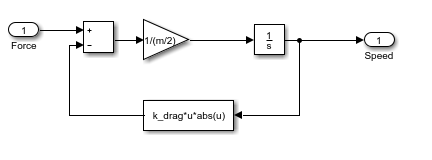
Просмотрите верхний уровень модели: Нажмите кнопку Up to Parent ![]() . Сделайте копию подсистемы, которую вы смоделировали, когда движущие силы для обоих колес являются тем же самым.
. Сделайте копию подсистемы, которую вы смоделировали, когда движущие силы для обоих колес являются тем же самым.
Вращательное Движение. Когда эти два колеса поворачиваются в противоположных направлениях, то есть, у них есть направлено противоположные скорости, они перемещаются в круг с радиусом r, вызывая вращательное движение. Когда они поворачиваются в том же направлении, нет никакого вращения. Поэтому учитывая, что скорости колеса всегда являются тем же самым в значении, это практично, чтобы смоделировать вращательное движение как зависящее от различия этих двух скоростей, VR и VL:
Создайте модель Rotation Dynamics:
В модели макета дважды кликните подсистему Вращения, чтобы отобразить пустую подсистему. Удалите связь между Inport и Выходным портом.
Угловая скорость модели и угол: Добавьте блок Integrator. Оставьте начальное условие как 0. Вывод этого блока является углом, тетой, и вход является угловой скоростью, theta_dot.
Вычислите угловую скорость из тангенциальной скорости. Добавьте Усиление с параметром 1/(2*r).
Установите связи между блоками можно следующим образом.

Просмотрите верхний уровень: Нажмите кнопку Up to Parent ![]() .
.
Опишите функцию от входа функции к ее выводу. Это описание может включать алгебраические уравнения и логические построения, которые можно использовать, чтобы создать графическую модель системы в Simulink.
Координатное Преобразование. Скорость робота в координатах X и Y, Vx и Vy, связана с линейной скоростью, Vn и углом можно следующим образом:
Создайте координатную модель преобразования:
В модели макета дважды кликните Координатную подсистему Преобразования, чтобы отобразить пустую подсистему.
Образцовые тригонометрические функции. Добавьте блок SinCos от библиотеки Math Operations.
Образцовое умножение. Добавьте два блока продукта от библиотеки Math Operations.
Установите связи между блоками как показано.
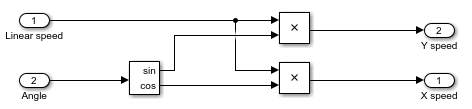
Просмотрите верхний уровень: Нажмите кнопку Up to Parent ![]() .
.
Источник для значений параметра модели может быть:
Записанные спецификации, такие как стандартные таблицы свойства или таблицы данных производителя
Прямые измерения в существующей системе
Оценки с помощью системного ввода/вывода
Модель использует эти параметры:
| Параметр | Символ | Значение/Модуль |
|---|---|---|
| Масса | m | 2,5 кг |
| Сопротивление качению | k_drag | 30 Ns2/m |
| Радиус робота | r | 0,15 м |
Simulink использует рабочую область MATLAB®, чтобы оценить параметры. Установите эти параметры в окне команды MATLAB:
m = 2.5; k_drag = 30; r = 0.15;
Валидируйте компоненты путем подачи входного сигнала и наблюдения выходного сигнала. Даже такая простая валидация может указать на мгновенные способы улучшить модель. Этот пример подтверждает следующее поведение:
Когда сила прикладывается постоянно к колесу, скоростные увеличения, пока она не достигает установившейся скорости.
Когда колеса поворачиваются в противоположных направлениях, угол постоянно увеличивается.
Создайте и запустите тестовую модель для компонента колеса:
Создайте модель. Кликните![]() и скопируйте блок Right Wheel в новую модель.
и скопируйте блок Right Wheel в новую модель.
Создайте тестовое воздействие в новой модели. Добавьте блок Step от библиотеки Sources. Соедините его с входом блока Right Wheel.
Добавьте средство просмотра в вывод. Щелкните правой кнопкой по выходному порту блока Right Wheel и выберите Create & Connect Viewer > Simulink > Scope.
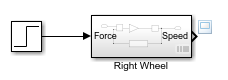
Запустите симуляцию. Щелкнуть![]() .
.
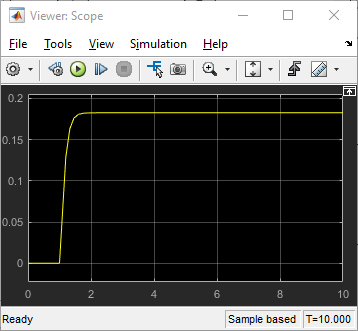
Результат симуляции показывает общее ожидаемое поведение. Нет никакого движения, пока сила не прикладывается во время шага. Когда сила прикладывается, скорость начинает увеличиваться и затем обосновывается в константе, когда приложенная сила и сила сопротивления достигают равновесия. Помимо валидации, эта симуляция также дает информацию о максимальной скорости колеса с данной силой.
Создайте и запустите тестовую модель для модели вращения:
Создайте модель. Кликните![]() и скопируйте блок Rotation в новую модель.
и скопируйте блок Rotation в новую модель.
Создайте тестовое воздействие в новой модели. Добавьте блок Step от библиотеки Sources. Соедините его с входом блока Rotation. Этот вход представляет различие скоростей колеса, когда колеса вращаются в противоположных направлениях.
Добавьте средство просмотра в вывод. Щелкните правой кнопкой по выходному порту блока Rotation и выберите Create & Connect Viewer > Simulink > Scope.

Запустите симуляцию. Щелкнуть![]() .
.
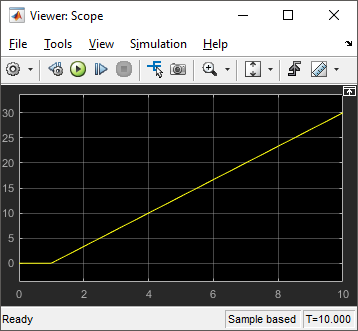
Эта симуляция показывает, что угол увеличивается постоянно, когда колеса поворачиваются с той же скоростью в противоположных направлениях. Можно сделать некоторые образцовые улучшения, чтобы облегчить интерпретировать угол вывод, например:
Можно преобразовать вывод в радианах до степеней. Добавьте блок Gain с усилением 180/pi.
Можно отобразить степени вывод в циклах 360 градусов. Добавьте блок Math Function с функциональным mod.
Тригонометрические функции MATLAB берут входные параметры в радианах.
После того, как вы валидируете компоненты, можно выполнить схожую валидацию на полной модели. Этот пример подтверждает следующее поведение:
Когда та же сила прикладывается к обоим колесам в том же направлении, перемещениям автомобиля в строке.
Когда та же сила прикладывается к обоим колесам в противоположных направлениях, автомобиль изменяет к лучшему себя.
В модели макета дважды кликните Входную подсистему, чтобы отобразить пустую подсистему.
Создайте тестовое воздействие путем добавления блока Step. Соедините его с обоими блоками Выходного порта.
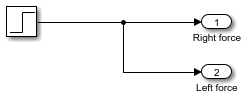
В верхнем уровне модели добавьте оба выходных сигнала в то же средство просмотра:
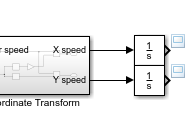
Запустите модель.
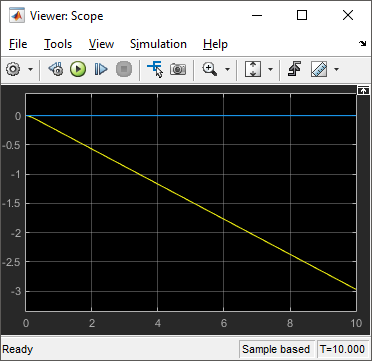
В этой фигуре желтая строка является направлением X, и синяя строка является направлением Y. Поскольку угол является нулем и не изменяется, автомобиль перемещается только в направление X, как ожидалось.
Дважды кликните Входную подсистему и добавьте Усиление с параметром -1 между источником и вторым выводом. Это инвертирует направление для левого колеса.
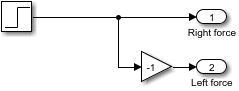
Добавьте осциллограф в угол вывод.
Запустите модель.
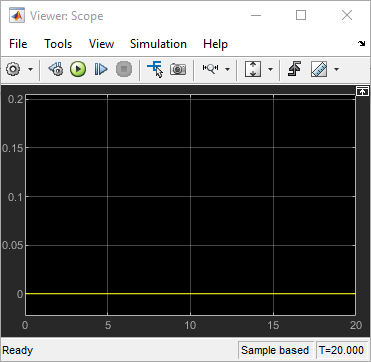
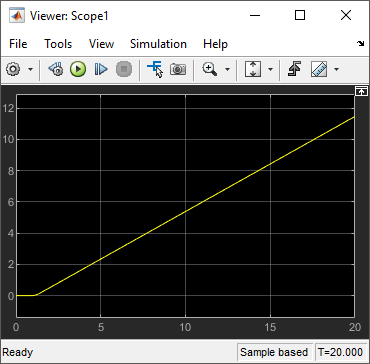
Первое представление показывает, что нет никакого движения в плоскости X-Y. Второе представление показывает, что существует устойчивое вращение.
Можно использовать эту итоговую модель, чтобы ответить на многие вопросы о модели путем изменения входа. Некоторые примеры:
Что происходит, когда начальный угол не является нулем?
Сколько времени занимает для движения остановиться, когда сила опускается до нуля?
Что происходит, когда робот более тяжел?
Что происходит, когда перемещения робота на более сглаженной поверхности, то есть, коэффициент сопротивления ниже?