Можно часто формулировать математическую систему, которую вы моделируете несколькими способами. Выбор математической модели лучшей формы позволяет симуляции выполняться быстрее и более точно. Например, рассмотрите простую схему серии RLC.
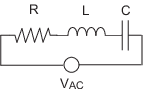
Согласно закону о напряжении Кирчофф, падение напряжения через эту схему равно сумме падения напряжения через каждый элемент схемы.
Используя закон Ома, чтобы решить для напряжения через каждый элемент схемы, уравнение для этой схемы может быть записано как
Можно смоделировать эту систему в Simulink® путем решения или для напряжения резистора или для напряжения индуктора. Который вы принимаете решение решить для влияния структуру модели и ее производительности.
Решение схемы RLC для урожаев напряжения резистора
Следующая схема показывает это уравнение, смоделированное в Simulink, где R является 70, C является 0.00003, и L является 0.04. Напряжение резистора является суммой источника напряжения, конденсаторного напряжения и напряжения индуктора. Вам нужен ток в схеме, чтобы вычислить напряжения конденсатора и индуктора. Чтобы вычислить ток, умножьте напряжение резистора на усиление 1/R. Вычислите конденсаторное напряжение путем интеграции тока и умножения усилением 1/C. Вычислите напряжение индуктора путем взятия производной тока и умножения усилением L.
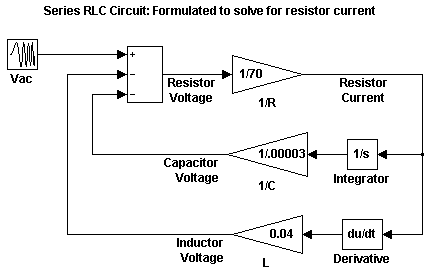
Эта формулировка содержит блок Derivative, сопоставленный с индуктором. Каждый раз, когда возможно, необходимо избежать математических формулировок, которые требуют Производных блоков, когда они вводят разрывы в систему. Численное интегрирование используется, чтобы решить образцовую динамику хотя время. Эти решатели интегрирования делают небольшие шаги в течение времени, чтобы удовлетворить ограничение точности на решение. Если разрыв, введенный блоком Derivative, является слишком большим, для решателя не возможно продвинуться через него.
Кроме того, в этой модели Производная, Сумма и два блока Усиления создают алгебраический цикл. Алгебраические циклы замедляют выполнение модели и могут произвести менее точные результаты симуляции. Смотрите Алгебраические Концепции Цикла для получения дополнительной информации.
Чтобы избегать использования блока Derivative, сформулируйте уравнение, чтобы решить для напряжения индуктора.
Следующая схема показывает это уравнение, смоделированное в Simulink. Напряжение индуктора является суммой источника напряжения, напряжения резистора и конденсаторного напряжения. Вам нужен ток в схеме, чтобы вычислить резистор и конденсаторные напряжения. Чтобы вычислить ток, интегрируйте напряжение индуктора и разделитесь на L. Вычислите конденсаторное напряжение путем интеграции тока и деления на C. Вычислите напряжение резистора путем умножения тока на усиление R.
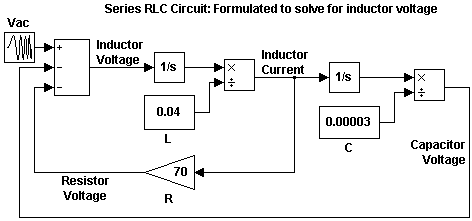
Эта модель содержит только блоки интегратора и никакие алгебраические циклы. В результате модель моделирует быстрее и более точно.