Образцовые дифференциальные алгебраические уравнения

Обзор примера реакции Робертсона

Робертсон [1] создал систему автокаталитических химических реакций протестировать и сравнить числовые решатели для жестких систем. Реакции, константы скорости (k), и скорости реакции (V) для системы даны можно следующим образом:

$\begin{matrix} A & \overset{k_{1}}{\to} & B & k_{1} = 0.04 & V_{1} = k_{1} [A] \\ B + B & \overset{k_{2}}{\to} & C + B & k_{2} = 3 \cdot 10^{7} & V_{2} = k_{2} [B] [B] \\ B + C & \overset{k_{3}}{\to} & A + C & k_{3} = 1 \cdot 10^{4} & V_{3} = k_{3} [B] [C] \end{matrix}$

Поскольку существуют значительные различия между скоростями реакции, числовые решатели рассматривают дифференциальные уравнения как жесткие. Для жестких дифференциальных уравнений некоторые числовые решатели не могут сходиться на решении, если размер шага не является чрезвычайно небольшим. Если размер шага является чрезвычайно небольшим, время симуляции может быть неприемлемо длинным. В этом случае необходимо использовать числовой решатель, разработанный, чтобы решить жесткие уравнения.

Модель Simulink от уравнений ОДУ

Система обыкновенных дифференциальных уравнений (ODE) имеет следующие характеристики:

Все уравнения являются обыкновенными дифференциальными уравнениями.
Каждое уравнение является производной зависимой переменной относительно одной независимой переменной, обычно время.
Количество уравнений равно количеству зависимых переменных в системе.

Используя скорости реакции, можно создать набор дифференциальных уравнений, описывающих скорость изменения каждой химической разновидности. С тех пор существует три разновидности, в математической модели существует три дифференциальных уравнения.

$\begin{array}{l} A^{'} = - 0.04 A + 1 \cdot^{104} B C \\ B^{'} = 0.04 A - 1 \cdot^{104} B C - 3 \cdot^{107} B^{2} \\ C^{'} = 3 \cdot^{107} B^{2} \end{array}$

Начальные условия: $A = 1$ , $B = 0$ , и $C = 0$ .

Создайте модель

Создайте модель или откройте модель ex_hb1ode.

Добавьте три блока Интегратора в свою модель. Маркируйте входные параметры A', B', и C', и выходными параметрами A, B и C соответственно.
Добавьте Сумму, продукт и блоки Усиления, чтобы решить каждую дифференциальную переменную. Например, чтобы смоделировать C' сигнала,
1. Добавьте блок Math Function и соедините вход, чтобы сигнализировать о B. Установите the Function параметр на square.
2. Соедините вывод от блока Math Function до блока Gain. Установите параметр Gain на 3e7.
3. Продолжите добавлять остающиеся условия дифференциального уравнения в свою модель.
Смоделируйте начальное условие A путем установки параметра Initial condition для блока A Integrator к 1.
Добавьте блоки, чтобы сохранить сигналы A, B и C к переменной MATLAB yout.

Моделируйте модель

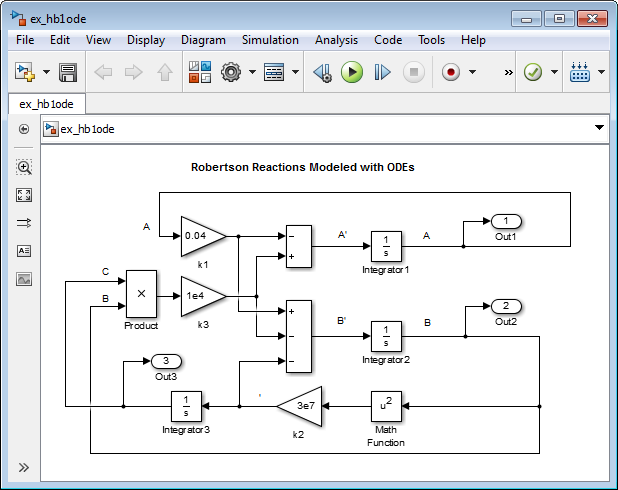
Создайте скрипт, который использует команду sim, чтобы моделировать вашу модель. Этот скрипт сохраняет результаты симуляции в переменной MATLAB yout. Поскольку симуляция имеет долговременный интервал, и B первоначально изменяется очень быстро, графический вывод значений на логарифмическом масштабе помогает визуально сравнить результаты. Кроме того, поскольку значение B является маленьким относительно значений A и C, умножьте B на $1 \cdot 10^{4}$ прежде, чем построить значения.

Введите следующие операторы в скрипт MATLAB^®. Если вы создали свою собственную модель, замена ex_hblode с именем вашей модели.
```
sim('ex_hb1ode')
yout(:,2) = 1e4*yout(:,2);
figure;
semilogx(tout,yout);
xlabel('Time');
ylabel('Concentration');
title('Robertson Reactions Modeled with ODEs')
```
Из меню Editor Simulink^® выберите Simulation> Model Configuration Parameters:
— В панели Решателя, набор Stop time к 4e5 и the Solver к ode15s (stiff/NDF).
— В панели Импорта Данных установите флажки Time и Output.
Запустите скрипт. Заметьте, что весь A преобразован в C.

Модель Simulink от уравнений ДАУ

Система дифференциальных алгебраических уравнений (DAE) имеет следующие характеристики:

Это содержит оба обыкновенных дифференциальных уравнения и алгебраические уравнения. Алгебраические уравнения не имеют никаких производных.
Только некоторые уравнения являются дифференциальными уравнениями, задающими производные некоторых зависимых переменных. Другие зависимые переменные заданы с алгебраическими уравнениями.
Количество уравнений равно количеству зависимых переменных в системе.

Некоторые системы содержат ограничения из-за законов сохранения, таких как сохранение массы и энергии. Если вы устанавливаете начальные концентрации на $A = 1$ , $B = 0$ , и $C = 0$ , общая концентрация трех разновидностей всегда равна $1$ с тех пор $A + B + C = 1$ . Можно заменить дифференциальное уравнение для $C^{'}$ со следующим алгебраическим уравнением, чтобы создать набор дифференциальных алгебраических уравнений (ДАУ).

$C = 1 - A - B$

Дифференциальные переменные A и B исключительно определяют алгебраическую переменную C.

$\begin{array}{l} A^{'} = - 0.04 A + 1 \cdot^{104} B C \\ B^{'} = 0.04 A - 1 \cdot^{104} B C - 3 \cdot^{107} B^{2} \\ C = 1 - A - B \end{array}$

Начальные условия: $A = 1$ и $B = 0$ .

Создайте модель

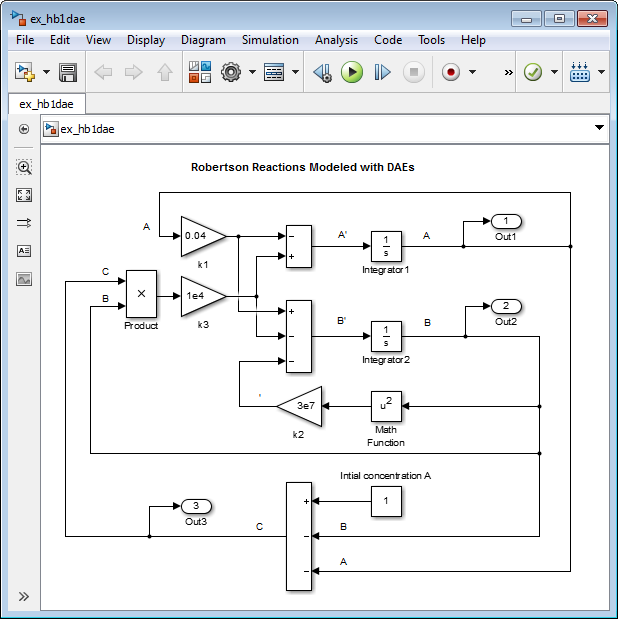
Внесите эти изменения в свою модель или в модель ex_hb1ode или откройте модель ex_hb1dae.

Удалите блок Integrator для вычисления C.
Добавьте блок Sum и установите параметр List of signs на + –.
Соедините сигналы A и B к минус входные параметры блока Sum.
Смоделируйте начальную концентрацию A с блоком Constant, соединенным с плюс вход блока Sum. Установите параметр Constant value to 1.
Соедините вывод блока Sum к разветвленному трубопроводу, соединенному с продуктом, и блокируется.

Моделируйте модель

Создайте скрипт, который использует команду sim, чтобы моделировать вашу модель.

Введите следующие операторы в скрипт MATLAB. Если вы создали свою собственную модель, замена ex_hbldae с именем вашей модели.
```
sim('ex_hb1dae')
yout(:,2) = 1e4*yout(:,2);
figure;
semilogx(tout,yout);
xlabel('Time');
ylabel('Concentration');
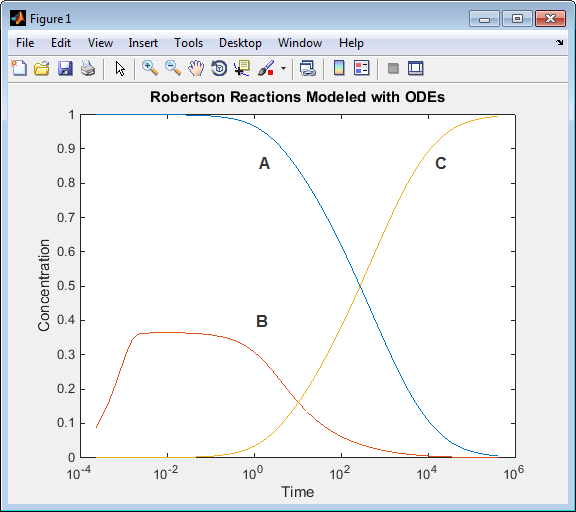
title('Robertson Reactions Modeled with DAEs')
```
Из меню Simulink Editor выберите Simulation> Model Configuration Parameters:
— В панели Решателя, набор Stop time к 4e5 и the Solver к ode15s (stiff/NDF).
— В панели Импорта Данных установите флажки Time и Output.
Запустите скрипт. Результаты симуляции, когда вы используете алгебраическое уравнение, эквивалентны для симуляции модели с помощью только дифференциальные уравнения.

Модель Simulink от уравнений ДАУ Используя блок алгебраического ограничения

Можно заменить дифференциальное уравнение для $C^{'}$ с алгебраическим уравнением, смоделированным с помощью блока Algebraic Constraint и блока Sum. Блок Algebraic Constraint ограничивает свой входной сигнал F (z) обнулять и выводит алгебраическое состояние z. Другими словами, блок вывод является значением, должен был произвести нуль во входе. Используйте следующее алгебраическое уравнение для входа к блоку.

$0 = A + B + C - 1$

Дифференциальные переменные A и B исключительно определяют алгебраическую переменную C.

$\begin{array}{l} A^{'} = - 0.04 A + 1 \cdot^{104} B C \\ B^{'} = 0.04 A - 1 \cdot^{104} B C - 3 \cdot^{107} B^{2} \\ C = 1 - A - B \end{array}$

Начальные условия: $A = 1$ , $B = 0$ , и $C = 1 \cdot 10^{- 3}$ .

Создайте модель

Внесите эти изменения в свою модель или в модель ex_hb1ode или откройте модель ex_hb1dae_acb.

Удалите блок Integrator для вычисления C.
Добавьте блок Algebraic Constraint. Установите параметр Initial guess на 1e-3.
Добавьте блок Sum. Установите параметр List of signs на – +++.
Соедините сигналы A и B к плюс входные параметры блока Sum.
Смоделируйте начальную концентрацию A с блоком Constant, соединенным с минус вход блока Sum. Установите параметр Constant value на 1.
Соедините вывод блока Algebraic Constraint к разветвленному трубопроводу, соединенному с продуктом и входными параметрами блока Out.
Создайте ответвление из вывода блока Algebraic Constraint к финалу плюс вход блока Sum.

Моделируйте модель

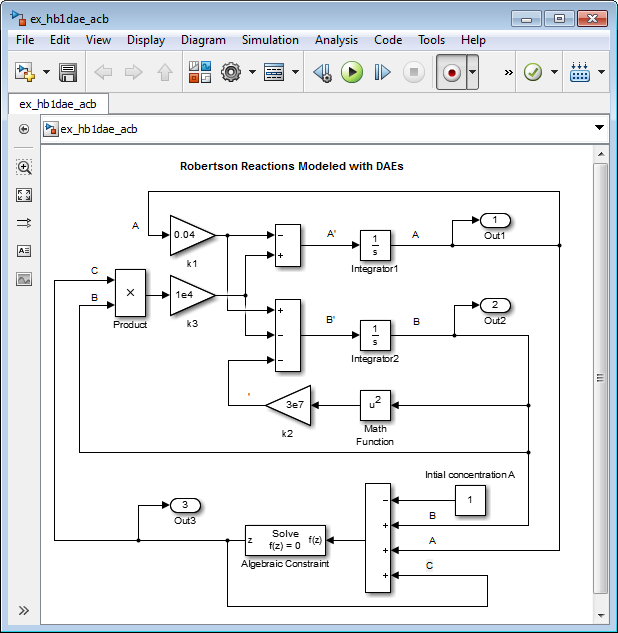
Создайте скрипт, который использует команду sim, чтобы моделировать вашу модель.

Введите следующие операторы в скрипт MATLAB. Если вы создали свою собственную модель, замена ex_hbl_acb с именем вашей модели.
```
sim('ex_hb1dae_acb')
yout(:,2) = 1e4*yout(:,2);
figure;
semilogx(tout,yout);
xlabel('Time');
ylabel('Concentration');
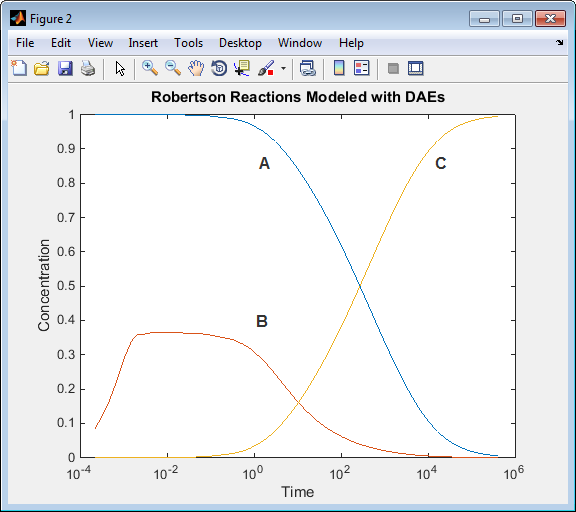
title('Robertson Reactions Modeled with DAEs and Algebraic Constraint Block')
```
Из меню Simulink Editor выберите Simulation> Model Configuration Parameters:
— В панели Решателя, набор Stop time к 4e5 и the Solver к ode15s (stiff/NDF).
— В панели Импорта Данных установите флажки Time и Output.
Запустите скрипт. Результаты симуляции, когда вы используете блок Algebraic Constraint, эквивалентны для симуляции модели с помощью только дифференциальные уравнения.

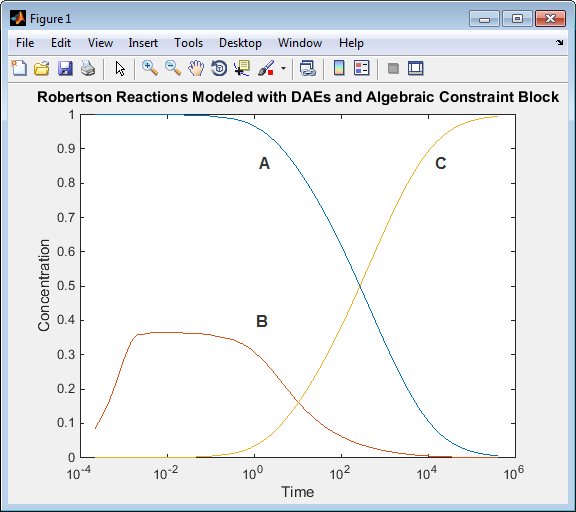
Используя Algebraic Constraint блок создает алгебраический цикл в модели, Если вы устанавливаете параметр Algebraic Loop на warning ( Simulation> Model Configuration Parameters> Diagnostics> Algebraic Loop), следующие индикаторы сообщения в Диагностическом Средстве просмотра во время симуляции.

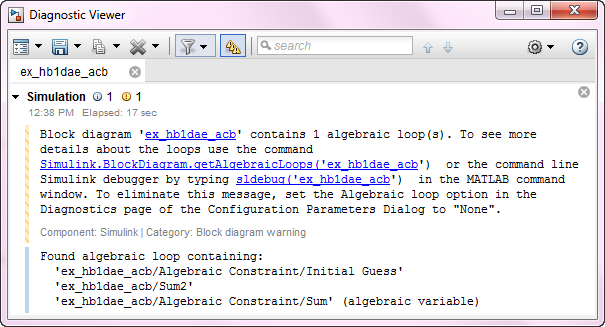
Для этой модели алгебраический решатель цикла смог найти решение для симуляции, но алгебраические циклы не всегда имеют решение, и они не поддержаны для генерации кода. Для получения дополнительной информации об алгебраических циклах в моделях Simulink и как удалить их, смотрите Алгебраические Концепции Цикла.

hb1ode hb1dae

Ссылки

[1] Робертсон, H. H. “Решение набора уравнений скорости реакции”. Числовой Анализ: Введение (редактор Дж. Уолша). Лондон, Нажатие England:Academic, 1966, стр 178–182.

Документация