Числа фиксированной точки используют целые числа и целочисленную арифметику, чтобы аппроксимировать вещественные числа. Они - действенные средства для выполнения вычислений, включающих вещественные числа, не требуя поддержки с плавающей точкой в базовом оборудовании системы.
Числа фиксированной точки представляют вещественные числа при помощи схемы кодирования:
V ≈ = S Q + B.
V является точным реальным значением, которое вы хотите аппроксимировать с номером фиксированной точки.
аппроксимированное реальное значение, которое следует из представления фиксированной точки.
Q является целым числом, которое кодирует номер фиксированной точки. Это значение называется квантованным целым числом.
S является коэффициентом, который определяет точность представления фиксированной точки. Это значение называется наклоном.
B является аддитивным исправлением, названным смещением.
Квантованный целочисленный Q является единственной частью представления фиксированной точки, которое отличается по значению. В сгенерированном коде количества S и B являются постоянными и появляются только как литеральные числа или выражения. Если номер фиксированной точки изменяется, его квантованные целочисленные изменения Q, но S и B остаются неизменными.
Определить квантованный целочисленный Q, соответствующий реальному значению V, вокруг количества (V – B)/S к целому числу. Например, чтобы представлять номер V = 15.345 в фиксированной точке с наклонным S = 0.5 и сместить B = 0.1, вы используете квантованное целое число
Q = вокруг ((V – B)/S) = вокруг ((15.345 – 0.1)/0.5) = раунд (30.49) = 30.
Поскольку вы вокруг Q к целому числу, вы теряете некоторую точность в представлении номера 15.345. Номер, который на самом деле представляет Q,
= S Q + B = 0,5 ⨉ 30 + 0.1 = 15.1.
Используя числа фиксированной точки, чтобы представлять вещественные числа с целыми числами включает потерю некоторой точности. Однако с подходящим выбором S и B, можно минимизировать эту потерю для допустимых уровней. Например, путем изменения схемы кодирования использовать S = 0.25 и B = 0.1, можно представлять номер V = 15.345 с большей точностью как:
Q = вокруг ((V – B)/S) = вокруг ((15.345 – 0.1)/0.25) = раунд (60.98) = 61
= S Q + B = 0,25 ⨉ 61 + 0.1 = 15.35.
Различием между![]() и V всегда являются меньше, чем наклонный S.
и V всегда являются меньше, чем наклонный S.
В Model Explorer можно задать кодирование фиксированной точки для объекта данных при помощи Ассистента Типа данных, как описано в Fixed-Point Data Properties. Установите поле Mode на Fixed point и задайте эти свойства:
Signedness: выберите Signed или Unsigned.
Word length: Задайте диаметр долота слова, которое содержит квантованный целочисленный Q.
Масштабирование: выберите Binary point или Slope and bias.
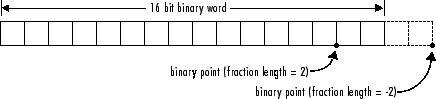
Если вы выбираете Binary point, Ассистент Типа данных отображает поле Fraction length, которое задает местоположение двоичной точки. Выбор Fraction length of n задает кодирование фиксированной точки с наклоном S = 2-n и смещение B = 0.
Если вы выбираете Slope and bias, Ассистент Типа данных отображает поля для ввода
S Slope и Bias
B для схемы кодирования фиксированной точки.
Также можно задать кодирование для объекта данных фиксированной точки непосредственно при помощи функции fixdt. В Property Inspector или Model Explorer, в поле Type, вводят выражение в один из этих форматов:
fixdt(Signed, WordLength, FractionLength)
fixdt(Signed, WordLength, Slope, Bias)
Некоторые схемы кодирования являются в вычислительном отношении дорогими, особенно в умножении и операциях деления. Выбор наклона, который является целочисленной степенью двойки и нулевым смещением, избегает этих в вычислительном отношении дорогих инструкций. Используя двоичную точку рекомендуется масштабирование.
Графики Stateflow® преобразовывают вещественные числа в числа фиксированной точки во время инициализации данных и как часть кастинга операций в приложении. Эти преобразования вычисляют квантованный целочисленный Q из входа вещественного числа. Тип преобразования зависит от языка действия для графика.
В графике, который использует MATLAB® в качестве языка действия, вы задаете метод для всех преобразований через свойства фиксированной точки для графика. Смотрите Свойства Фиксированной точки.
Например, если вы устанавливаете свойство MATLAB Chart fimath на Same as MATLAB, затем график округляет получившееся квантованное целое число к своему самому близкому целочисленному значению.
Графики, которые используют C в качестве языка действия, используют два метода для преобразования данных фиксированной точки:
Оффлайновые преобразования инициализируют данные во время генерации кода. Оффлайновые преобразования разработаны, чтобы максимизировать точность. Эти преобразования вокруг получившегося квантованного целого числа к его самому близкому целочисленному значению. Оффлайновые преобразования выполняются для инициализации данных (переменные и константы) в иерархии Stateflow и от рабочего пространства MATLAB.
Онлайновые преобразования выполняют операции кастинга в течение времени выполнения. Онлайновые преобразования разработаны, чтобы максимизировать вычислительную эффективность. Они быстрее и более эффективны, но менее точны, чем оффлайновые преобразования. Вместо того, чтобы округлить Q к его самому близкому целому числу, онлайновые преобразования вокруг в пол (за исключением деления, которое может вокруг к 0, в зависимости от компилятора C).
Например, эта таблица иллюстрирует различие между оффлайновыми и онлайновыми преобразованиями вещественных чисел к числам фиксированной точки, заданным с наклоном S = 2-4 и смещение B = 0. Для каждого реального значения V график вычисляет квантованный целочисленный Q путем округления (V-B)/S к самому близкому целому числу (в оффлайновом преобразовании) или на пол (в онлайновом преобразовании). Для каждого преобразования, = Q S + B является аппроксимированным реальным значением, следующим из Q.
| Реальное значение | Оффлайновое преобразование | Онлайновое преобразование | |||
|---|---|---|---|---|---|
V | (V-B)/S | Q | Q | ||
15.345 | 245.52 | 246 | 15.375 | 245 | 15.3125 |
3.45 | 55.2 | 55 | 3.4375 | 55 | 3.4375 |
1.0375 | 16.6 | 17 | 1.0625 | 16 | 1 |
2.06 | 32.96 | 33 | 2.0625 | 32 | 2 |
В графиках, которые используют C в качестве языка действия, можно избежать явных бросков типа при помощи фиксированной точки контекстно-зависимые константы. Эти константы выводят свой тип из контекста, в котором они происходят. Они записаны как обычные числа с суффиксным C или c. Например, 4.3C и 123.4c являются допустимой фиксированной точкой контекстно-зависимые константы, которые можно использовать в операторах действия.
Несмотря на то, что фиксированная точка, контекстно-зависимые константы могут появиться в выражениях с любыми типами данных (включая целые числа и данные с плавающей точкой), их основное использование, с числами фиксированной точки. Алгоритм, который интерпретирует контекстно-зависимую константу, вычисляет тип, который обеспечивает максимальную точность без переполнения. Алгоритм зависит от:
Операции в выражении
Другие типы данных в контексте
Значение константы
Фиксированная точка контекстно-зависимые константы выводит их тип согласно этим правилам:
В операции кастинга константа имеет тип, к которому она бросается.
В простой операции присвоения формы a = b:
Если b является контекстно-зависимой константой, он имеет тот же тип как a.
Если b является операцией сложения или операцией вычитания, то константа имеет тот же тип как другой операнд.
Если b является умножением или операцией деления с операндом фиксированной точки, то константа имеет тип, который обеспечивает самую лучшую точность для результата фиксированной точки, как определено функцией fixptbestexp.
Если b является умножением или операцией деления с операндом с плавающей точкой типа double или single, то константа имеет тот же тип как операнд с плавающей точкой.
В специальной операции присвоения формы a := b:
Если b является контекстно-зависимой константой, он имеет тот же тип как a.
Если b является арифметической операцией с операндом с плавающей точкой типа double или single, или если a является объектом данных с плавающей точкой, то константа имеет тот же тип как число с плавающей запятой.
Если b является операцией сложения или операцией вычитания с операндом фиксированной точки, и a является объектом данных фиксированной точки, то константа имеет тот же тип как a.
Если b является умножением или операцией деления с операндом фиксированной точки, и a является объектом данных фиксированной точки, то константа имеет тип, который обеспечивает самую лучшую точность для результата фиксированной точки.
В качестве аргумента в вызове функции константа имеет тот же тип в качестве формального аргумента.
Вы не можете использовать контекстно-зависимые константы в качестве обоих операндов бинарной операции или как крайний левый операнд операции присвоения.
Разработайте и протестируйте свое приложение при помощи двойного - или числа с плавающей запятой с одинарной точностью. Используя двойной - или числа с плавающей запятой с одинарной точностью не ограничивает область значений или точность ваших вычислений. Если ваше приложение работает, как разработано, можно начать заменять данными фиксированной точки данные с двойной точностью.
В диалоговом окне Model Configuration Parameters, на панели Hardware Implementation, устанавливает целочисленный размер слова для среды симуляции к целочисленному размеру намеченного целевого окружения. Код, сгенерированный Stateflow, использует этот целочисленный размер, чтобы выбрать типы результата для ваших операций фиксированной точки. Смотрите Панель Аппаратной реализации (Simulink).
Когда вы моделируете свою модель, используйте обнаружение переполнения, чтобы предупредить вас, когда результат операции фиксированной точки превышает числовую способность своей фиксированной точки. В диалоговом окне Model Configuration Parameters, на Diagnostics> панель Data Validity, устанавливает Wrap on overflow и Saturate on overflow к error или warning. Если вы сталкиваетесь с ошибками переполнения в данных фиксированной точки, увеличиваете область значений ваших данных:
Увеличение значения Word length для переполняющихся данных фиксированной точки. Например, изменитесь, количество битов раньше кодировало данные фиксированной точки от 16 до 32. Это действие изменяет основной целочисленный тип для Q от int16 до int32.
Уменьшение значения Fraction length (при использовании масштабирования Binary point) или увеличение значения Slope (при использовании масштабирования Slope and bias). Например, уменьшите значение Fraction length с 4 до 1 (или, эквивалентно, увеличьте значение Slope от S = 2-4 = 0.0625 к S = 2-1 = 0.5). Это действие увеличивает область значений ваших данных фиксированной точки, но уменьшает доступную точность.
Для получения дополнительной информации смотрите Нарушения Области значений Данных.
Если вы сталкиваетесь с проблемами с поведением модели, происходящим от несоответствующей точности в ваших данных фиксированной точки, увеличиваете точность ваших данных путем увеличения значения Fraction length (при использовании масштабирования Binary point) или уменьшение значения Slope (при использовании масштабирования Slope and bias). Например, увеличьте значение Fraction length от 2 до 3 (или, эквивалентно, уменьшите значение Slope с S = 2-2 = 0.25 к S = 2-3 = 0.125). Это действие увеличивает точность ваших данных фиксированной точки, но уменьшает доступную область значений.
В графиках, которые используют C в качестве языка действия, можно использовать специальную операцию := присвоения и контекстно-зависимые константы, чтобы поддержать как можно больше точности. Смотрите Продвижение Фиксированной точки Переопределения в Графиках C и Фиксированной точке Контекстно-зависимые Константы.
Если вы не используете контекстно-зависимые константы с фиксированными точками, нецелое число числовые константы (константы, которые имеют десятичную точку), может обеспечить операции фиксированной точки, чтобы привести к результатам с плавающей точкой.
Инструменты автоматического масштабирования могут изменить настройки данных фиксированной точки Stateflow. Можно предотвратить автоматическое масштабирование путем выбора установки типа данных Блокировки против изменений опцией Fixed-Point Tool для объекта данных фиксированной точки. Смотрите Тип данных Блокировки Против Fixed-Point Tool. Для методов при автомасштабировании данных фиксированной точки смотрите Выбор Range Collection Method (Fixed-Point Designer).
Совместно использовать данные фиксированной точки с моделями Simulink®:
Используйте те же значения свойств, чтобы задать данные в диаграмме Stateflow и в модели Simulink. Для примера этого метода совместного использования входных данных из модели Simulink с помощью блока Gateway In см. Модель Контроллер Скорострельного оружия при помощи Входных параметров Фиксированной точки.
Для некоторых блоков Simulink можно задать тип данных о вводе или выводе непосредственно. Например, можно задать тип данных с фиксированной точкой для блока Constant непосредственно в поле Output data type при помощи функции fixdt.
Задайте данные как Ввод или вывод в диаграмме Stateflow и дайте команду отправке или получению блока в модели Simulink наследовать свой тип от данных о графике. Во многих блоках можно установить типы данных посредством наследования от ведущего блока, или посредством обратного распространения от следующего блока. Можно установить тип данных блока Simulink совпадать с типом данных порта Stateflow, с которым это соединяется.
Например, можно установить блок Constant наследовать свой тип от порта Stateflow Input to Simulink, который он предоставляет. Установите параметры блоков Output data type на Inherit via back propagation.
Диаграммы Stateflow задают типы данных с фиксированной точкой от значений, которые вы задаете для S, B и основного целочисленного типа для Q.
Для каждых данных фиксированной точки график задает целочисленную переменную для Q в сгенерированном коде. Это целое число является единственной частью номера фиксированной точки, который изменяется в значении. Доступные базовые типы для Q являются типами беззнаковых целых чисел uint8, uint16 и uint32, и целое число со знаком вводит int8, int16 и int32. Если номер фиксированной точки имеет наклонный S = 1 и смещение B = 0, это эквивалентно своему квантованному целочисленному Q и ведет себя точно как его основной целочисленный тип.
Наклонный S включен в коэффициент F с 1 ≤ F <2 и целочисленная степень двойки с экспонентой E:
S = F ⨉ 2E.
Если дробный наклонный F больше, чем 1, он преобразован в номер фиксированной точки. Схемы кодирования с F> 1 могут быть в вычислительном отношении дорогими, особенно в умножении и операциях деления. Установка F = 1 избегает этих в вычислительном отношении дорогих инструкций. В этой установке, масштабирующейся степенью 2, реализован как сдвиги разряда, которые более эффективны, чем умножают инструкции. Поэтому использование единственного двоичной точкой масштабирования, в который F = 1 и B = 0, рекомендуется.
Операции для фиксированных точек реализованы с решениями для квантованного целого числа, как описано в Арифметических операциях для Данных Фиксированной точки. Чтобы сгенерировать эффективный код, правила продвижения фиксированной точки выбирают значения для наклона и смещения, которые отменяют трудные условия в решениях. См. Правила Продвижения для Операций Фиксированной точки.