Проект поля-Behnken
dBB = bbdesign(n)
[dBB,blocks] = bbdesign(n)
[...] = bbdesign(n,param,val)
dBB = bbdesign(n) генерирует проект Поля-Behnken для факторов n. n должен быть целочисленный 3 или больше. dBB выходной матрицы является m-by-n, где m является количеством выполнений в проекте. Каждая строка представляет запущенный тот с настройками для всех факторов, представленных в столбцах. Факторные значения нормированы так, чтобы точки куба приняли значения между -1 и 1.
[dBB,blocks] = bbdesign(n) запрашивает блокированный проект. Выводом blocks является m-by-1 вектор номеров блока для каждого выполнения. Блоки указывают на выполнения, которые должны быть измерены при подобных условиях минимизировать эффект межблочных различий на оценках параметра.
[...] = bbdesign(n, задает одну или несколько дополнительных пар параметра/значения для проекта. В следующей таблице перечислены допустимые пары параметра/значения.param,val)
| Параметр | Описание | Значения |
|---|---|---|
'center' | Количество центральных точек. | Целое число. Значение по умолчанию зависит от |
'blocksize' | Максимальное количество точек на блок. | Целое число. Значением по умолчанию является |
Следующее создает проект Поля-Behnken с 3 факторами:
dBB = bbdesign(3)
dBB =
-1 -1 0
-1 1 0
1 -1 0
1 1 0
-1 0 -1
-1 0 1
1 0 -1
1 0 1
0 -1 -1
0 -1 1
0 1 -1
0 1 1
0 0 0
0 0 0
0 0 0Центральная точка запущена 3 раза, чтобы допускать более универсальную оценку отклонения прогноза по целому пробелу проекта.
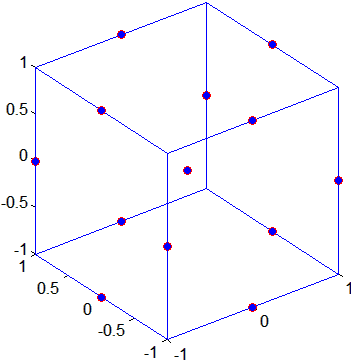
Визуализируйте проект можно следующим образом:
plot3(dBB(:,1),dBB(:,2),dBB(:,3),'ro',...
'MarkerFaceColor','b')
X = [1 -1 -1 -1 1 -1 -1 -1 1 1 -1 -1; ...
1 1 1 -1 1 1 1 -1 1 1 -1 -1];
Y = [-1 -1 1 -1 -1 -1 1 -1 1 -1 1 -1; ...
1 -1 1 1 1 -1 1 1 1 -1 1 -1];
Z = [1 1 1 1 -1 -1 -1 -1 -1 -1 -1 -1; ...
1 1 1 1 -1 -1 -1 -1 1 1 1 1];
line(X,Y,Z,'Color','b')
axis square equal