Создайте агломерационные кластеры из данных
T = clusterdata(X,cutoff)T = clusterdata(X,Name,Value)T = clusterdata(X,cutoff)X, учитывая порог cutoff для сокращения агломерационного иерархического дерева, которое функция linkage генерирует от X.
clusterdata поддерживает агломерационную кластеризацию и включает pdist, linkage и функции cluster, которые можно использовать отдельно для более детального анализа. Дополнительную информацию см. в Описании Алгоритма.
T = clusterdata(X,Name,Value)'Maxclust',5, чтобы найти максимум пяти кластеров.
Найдите и визуализируйте максимум трех кластеров в случайным образом сгенерированном наборе данных с помощью двух разных подходов:
Задайте значение для входного параметра cutoff.
Задайте значение для аргумента пары "имя-значение" 'MaxClust'.
Создайте набор выборочных данных, состоящий из случайным образом сгенерированных данных из трех стандартных равномерных распределений.
rng('default'); % For reproducibility X = [gallery('uniformdata',[10 3],12); ... gallery('uniformdata',[10 3],13)+1.2; ... gallery('uniformdata',[10 3],14)+2.5]; y = [ones(10,1);2*(ones(10,1));3*(ones(10,1))]; % Actual classes
Создайте график рассеивания данных.
scatter3(X(:,1),X(:,2),X(:,3),100,y,'filled') title('Randomly Generated Data in Three Clusters');
Найдите максимум трех кластеров в данных путем определения значения 3 для входного параметра cutoff.
T1 = clusterdata(X,3);
Поскольку значение cutoff больше, чем 2, clusterdata интерпретирует cutoff как максимальное количество кластеров.
Отобразите данные на графике с получившимися кластерными присвоениями.
scatter3(X(:,1),X(:,2),X(:,3),100,T1,'filled') title('Result of Clustering');
Найдите максимум трех кластеров путем определения значения 3 для аргумента пары "имя-значение" 'MaxClust'.
T2 = clusterdata(X,'Maxclust',3); Отобразите данные на графике с получившимися кластерными присвоениями.
scatter3(X(:,1),X(:,2),X(:,3),100,T2,'filled') title('Result of Clustering');
Используя оба подхода, clusterdata идентифицирует три отличных кластера в данных.
Создайте иерархическое кластерное дерево и найдите кластеры за один шаг. Визуализируйте кластеры с помощью 3-D графика рассеивания.
Создайте 20,000 3 матрица выборочных данных, сгенерированных от стандартного равномерного распределения.
rng('default'); % For reproducibility X = rand(20000,3);
Найдите максимум четырех кластеров в иерархическом кластерном дереве созданным с помощью метода связи ward. Задайте 'SaveMemory' как 'on', чтобы создать кластеры, не вычисляя матрицу расстояния. В противном случае можно получить ошибку из памяти, если машина не имеет достаточной памяти, чтобы содержать матрицу расстояния.
T = clusterdata(X,'Linkage','ward','SaveMemory','on','Maxclust',4);
Отобразите данные на графике с каждым кластером, отображенным различным цветом.
scatter3(X(:,1),X(:,2),X(:,3),10,T)
clusterdata идентифицирует четыре кластера в данных.
Если 'Linkage' является 'centroid' или 'median', то linkage может произвести кластерное дерево, которое не является монотонным. Этот результат происходит, когда расстояние от объединения двух кластеров, r и s, к третьему кластеру является меньше, чем расстояние между r и s. В этом случае, в древовидной схеме, чертившей с ориентацией по умолчанию, путь от листа до корневого узла делает некоторые нисходящие шаги. Чтобы избежать этого результата, задайте другое значение для 'Linkage'. Следующее изображение показывает немонотонное кластерное дерево.
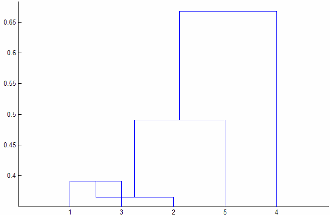
В этом случае к кластеру 1 и кластеру 3 соединяют в новый кластер, в то время как расстояние между этим новым кластером и кластером 2 является меньше, чем расстояние между кластером 1 и кластером 3.
Если вы задаете значение c для входного параметра cutoff, то T = clusterdata(X,c)
Создайте вектор Евклидова расстояния между парами наблюдений в X при помощи pdist.
Y = pdist(X,'euclidean')
Создайте агломерационное иерархическое кластерное дерево из Y при помощи linkage с методом 'single' для вычисления кратчайшего расстояния между кластерами.
Z = linkage(Y,'single')
Если 0 < c < 2, используйте cluster, чтобы задать кластеры от Z, когда противоречивые значения будут меньше, чем c.
T = cluster(Z,'Cutoff',c)
Если c является целочисленным значением ≥ 2, используйте cluster, чтобы найти максимум кластеров c от Z.
T = cluster(Z,'MaxClust',c)
Если у вас есть иерархический кластерный древовидный Z (вывод функции linkage для матрицы входных данных X), можно использовать cluster, чтобы выполнить агломерационную кластеризацию на Z и возвратить кластерное присвоение для каждого наблюдения (строка) в X.
cluster | dendrogram | inconsistent | kmeans | linkage | pdist