Quasi-random number generators (QRNGs) производит очень универсальные выборки единичного гиперкуба. QRNGs минимизируют discrepancy между распределением сгенерированных точек и распределением с равными пропорциями точек в каждом подкубе универсального раздела гиперкуба. В результате QRNGs систематически заполняют “дыры” в любом начальном сегменте сгенерированной квазислучайной последовательности.
В отличие от псевдослучайных последовательностей, описанных в общих Методах Генерации Псевдослучайного числа, квазислучайные последовательности проваливают много статистических тестов на случайность. Приближение истинной случайности, однако, не является их целью. Квазислучайные последовательности стремятся заполнить пробел однородно и сделать так таким способом, которым начальные сегменты аппроксимируют это поведение до заданной плотности.
Приложения QRNG включают:
Интегрирование квази-Монте-Карло (QMC). Методы Монте-Карло часто используются, чтобы оценить трудные, многомерные интегралы без решения закрытой формы. QMC использует квазислучайные последовательности, чтобы улучшить свойства сходимости этих методов.
Заполнение экспериментальных планов. Во многих экспериментальных настройках проведение измерений при каждой факторной установке является дорогим или неосуществимым. Квазислучайные последовательности обеспечивают эффективную, универсальную выборку пробела проекта.
Глобальная оптимизация. Алгоритмы оптимизации обычно находят локальный оптимум в окружении начального значения. При помощи квазислучайной последовательности начальных значений, ищет глобальные оптимумы, однородно выбирают бассейны привлекательности всех локальных минимумов.
Вообразите простую 1D последовательность, которая производит целые числа от 1 до 10. Это - основная последовательность, и первыми тремя точками является [1,2,3]:
![]()
Теперь посмотрите на то, как Scramble, Skip и Leap работают совместно:
Scramble — Скремблирование переставляет точки одним из нескольких различных способов. В этом примере примите, что скремблирование превращает последовательность в 1,3,5,7,9,2,4,6,8,10. Первыми тремя точками является теперь [1,3,5]:
![]()
Skip — Значение Skip задает количество начальных точек, чтобы проигнорировать. В этом примере, установленном значение Skip к 2. Последовательностью является теперь 5,7,9,2,4,6,8,10, и первыми тремя точками является [5,7,9]:
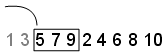
Leap — Значение Leap задает число точек, чтобы проигнорировать для каждого, которого вы берете. При продолжении примера с набором Skip к 2, если вы устанавливаете Leap на 1, последовательность использует любую точку. В этом примере последовательностью является теперь 5,9,4,8, и первыми тремя точками является [5,9,4]:
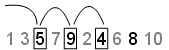
Функции Statistics and Machine Learning Toolbox™ поддерживают эти квазислучайные последовательности:
Последовательности Холтона. Произведенный функцией haltonset. Эти последовательности используют различные главные основы, чтобы сформировать последовательно более прекрасные универсальные разделы единичного интервала в каждой размерности.
Последовательности Sobol. Произведенный функцией sobolset. Эти последовательности используют основу 2, чтобы сформировать последовательно более прекрасные универсальные разделы единичного интервала, и затем переупорядочить координаты в каждой размерности.
Латинские последовательности гиперкуба. Произведенный функцией lhsdesign. Хотя не квазислучайный в смысле минимизации несоответствия, эти последовательности, тем не менее, производят разреженные универсальные выборки, полезные в экспериментальных планах.
Квазислучайные последовательности являются функциями от положительных целых чисел до единичного гиперкуба. Чтобы быть полезным в приложении, начальный point set последовательности должен быть сгенерирован. Укажите, что наборы являются матрицами размера n-by-d, где n является числом точек, и d является размерностью выбираемого гиперкуба. Функции haltonset и sobolset создают наборы точки со свойствами заданной квазислучайной последовательности. Начальные сегменты наборов точки сгенерированы методом net haltonset и классов sobolset, но точки могут быть сгенерированы и получены доступ в более общем плане использующая индексация круглой скобки.
Из-за пути, которым сгенерированы квазислучайные последовательности, они могут содержать нежелательные корреляции, особенно в их начальных сегментах, и особенно в более высоких размерностях. Чтобы решить эту проблему, квазислучайная точка часто устанавливает skip, leap или значения scramble в последовательности. haltonset и функции sobolset позволяют вам задавать и Skip и свойство Leap квазислучайной последовательности, и метод scramble haltonset и классов sobolset позволяет вам, применяют множество борющихся методов. Скремблирование уменьшает корреляции, также улучшая однородность.
Этот пример показывает, как использовать haltonset, чтобы создать 2D набор квазислучайной точки Холтона.
Создайте объект haltonset p, который пропускает первые 1 000 значений последовательности и затем сохраняет каждую 101-ю точку.
rng default % For reproducibility p = haltonset(2,'Skip',1e3,'Leap',1e2)
p =
Halton point set in 2 dimensions (89180190640991 points)
Properties:
Skip : 1000
Leap : 100
ScrambleMethod : none
Объект p инкапсулирует свойства заданной квазислучайной последовательности. Набор точки конечен с длиной, определенной свойствами Skip и Leap и пределами на размере индексов набора точки.
Используйте scramble, чтобы применить скремблирование противоположного основания.
p = scramble(p,'RR2')p =
Halton point set in 2 dimensions (89180190640991 points)
Properties:
Skip : 1000
Leap : 100
ScrambleMethod : RR2
Используйте net, чтобы сгенерировать первые 500 точек.
X0 = net(p,500);
Это эквивалентно
X0 = p(1:500,:);
Значения точки устанавливают X0, не сгенерированы и сохранены в памяти, пока вы не получаете доступ к p с помощью индексации круглой скобки или net.
Чтобы ценить природу квазислучайных чисел, создайте график рассеивания этих двух размерностей в X0.
scatter(X0(:,1),X0(:,2),5,'r') axis square title('{\bf Quasi-Random Scatter}')

Сравните это с рассеянием универсальных псевдослучайных чисел, сгенерированных функцией rand.
X = rand(500,2); scatter(X(:,1),X(:,2),5,'b') axis square title('{\bf Uniform Random Scatter}')

Квазислучайное рассеяние кажется более универсальным, избегая сбора в группу в псевдослучайном рассеянии.
В статистическом смысле квазислучайные числа слишком универсальны, чтобы пройти традиционные тесты случайности. Например, тест Кольмогорова-Смирнова, выполняемый kstest, используется, чтобы оценить, имеет ли набор точки универсальное случайное распределение. Когда выполняется неоднократно на универсальных псевдослучайных выборках, таких как сгенерированные rand, тест производит равномерное распределение p-значений.
nTests = 1e5; sampSize = 50; PVALS = zeros(nTests,1); for test = 1:nTests x = rand(sampSize,1); [h,pval] = kstest(x,[x,x]); PVALS(test) = pval; end histogram(PVALS,100) h = findobj(gca,'Type','patch'); xlabel('{\it p}-values') ylabel('Number of Tests')

Результаты очень отличаются, когда тест неоднократно выполняется на универсальных квазислучайных выборках.
p = haltonset(1,'Skip',1e3,'Leap',1e2); p = scramble(p,'RR2'); nTests = 1e5; sampSize = 50; PVALS = zeros(nTests,1); for test = 1:nTests x = p(test:test+(sampSize-1),:); [h,pval] = kstest(x,[x,x]); PVALS(test) = pval; end histogram(PVALS,100) xlabel('{\it p}-values') ylabel('Number of Tests')

Маленькие p-значения подвергают сомнению нулевую гипотезу, что данные равномерно распределены. Если гипотеза будет верна, приблизительно 5% p-значений, как ожидают, упадут ниже 0.05. Результаты удивительно сопоставимы в своем отказе бросить вызов гипотезе.
Квазислучайный streams, произведенный функцией qrandstream, используется, чтобы сгенерировать последовательные квазислучайные выходные параметры, вместо того, чтобы указать наборы определенного размера. Потоки используются как псевдоrng, такие как rand, когда клиентские приложения требуют источника квазислучайных чисел неопределенного размера, к которому можно получить доступ периодически. Свойства квазислучайного потока, такие как его тип (Холтон или Sobol), размерность, пропуск, прыжок, и скремблирование, установлены, когда поток создается.
В реализации квазислучайные потоки являются по существу очень большими наборами квазислучайной точки, хотя к ним получают доступ по-другому. state квазислучайного потока является скалярным индексом следующего вопроса, который будет взят из потока. Используйте метод qrand класса qrandstream, чтобы сгенерировать точки от потока, начинающего с текущего состояния. Используйте метод reset, чтобы сбросить состояние к 1. В отличие от наборов точки, потоки не поддерживают индексацию круглой скобки.
Этот пример показывает, как сгенерировать выборки от набора квазислучайной точки.
Используйте haltonset, чтобы создать квазислучайную точку, устанавливает p, затем неоднократно постепенно увеличиваются, индекс в точку установил test генерировать различные выборки.
p = haltonset(1,'Skip',1e3,'Leap',1e2); p = scramble(p,'RR2'); nTests = 1e5; sampSize = 50; PVALS = zeros(nTests,1); for test = 1:nTests x = p(test:test+(sampSize-1),:); [h,pval] = kstest(x,[x,x]); PVALS(test) = pval; end
Те же результаты получены при помощи qrandstream, чтобы создать квазислучайный поток, q на основе точки установил p и разрешение потоку заботиться о шаге к индексу.
p = haltonset(1,'Skip',1e3,'Leap',1e2); p = scramble(p,'RR2'); q = qrandstream(p); nTests = 1e5; sampSize = 50; PVALS = zeros(nTests,1); for test = 1:nTests X = qrand(q,sampSize); [h,pval] = kstest(X,[X,X]); PVALS(test) = pval; end