В статистике effect - что-либо, что влияет на значение переменной отклика при конкретной установке переменных прогноза. Эффекты переводятся в параметры модели. В линейных моделях эффекты становятся коэффициентами, представляя пропорциональные вклады образцовых условий. В нелинейных моделях эффекты часто имеют определенные физические интерпретации и появляются в более общих нелинейных комбинациях.
Fixed effects представляет параметры генеральной совокупности, принятые, чтобы быть тем же каждым разом, когда данные собраны. Оценка фиксированных эффектов является традиционной областью моделирования регрессии. Random effects, для сравнения, является демонстрационно-зависимыми случайными переменными. В моделировании должны быть заданы случайное действие эффектов как дополнительные остаточные члены, и их дистрибутивы и ковариации.
Например, рассмотрите модель устранения препарата от кровотока. Модель использует время t в качестве предиктора и концентрации препарата C как ответ. Нелинейный образцовый термин C 0e–rt комбинирует параметры C 0 и r, представление, соответственно, начальная концентрация и уровень устранения. Если данные собраны через несколько человек, разумно принять, что уровень устранения является случайной переменной r i в зависимости от отдельного i, отличающегося вокруг среднего значения генеральной совокупности . Термин C 0e–rt становится
где β = фиксированный эффект и b i = случайный эффект.
Случайные эффекты полезны, когда данные попадают в естественные группы. В модели устранения препарата группы являются просто людьми при исследовании. Более сложные модели могут сгруппировать данные возрастом человека, весом, диетой, и т.д. Несмотря на то, что группы не являются особым вниманием исследования, добавляя, что случайные эффекты к модели расширяют надежность выводов вне определенной выборки людей.
Счет Mixed-effects models и зафиксированные и случайные эффекты. Как со всеми моделями регрессии, их цель состоит в том, чтобы описать переменную отклика как функцию переменных прогноза. Модели смешанных эффектов, однако, распознают корреляции в демонстрационных подгруппах. Таким образом они обеспечивают компромисс между игнорированием групп данных полностью и подбором кривой каждой группе с отдельной моделью.
Предположим, что данные для нелинейной модели регрессии попадают в один из m отличные группы i = 1..., m. Чтобы составлять группы в модели, напишите ответу j в группе i как:
y i, j является ответом, x i j, является вектором предикторов, φ, является вектором параметров модели и ε i, j является ошибкой измерения или процесса. Индексный j колеблется от 1 до n i, где n i является количеством наблюдений в группе i. Функциональный f задает форму модели. Часто, x i j является просто временем наблюдения t i j. Ошибки обычно принимаются, чтобы быть независимыми и тождественно, нормально распределенными, с постоянным отклонением.
Оценки параметров в φ описывают генеральную совокупность, принимая, что те оценки являются тем же самым для всех групп. Если, однако, оценки отличаются группой, модель становится
В модели смешанных эффектов φ i может быть комбинацией фиксированного и случайного эффекта:
Случайные эффекты b i обычно описываются как многомерные нормально распределенный со средним нулем и ковариацией Ψ. Оценка фиксированных эффектов, β и ковариация случайных эффектов Ψ предоставляют описание генеральной совокупности, которая не принимает параметры φ, i является тем же самым через группы. При оценке случайных эффектов b i также дает описание определенных групп в данных.
Параметры модели не должны быть идентифицированы с отдельными эффектами. В целом design matrices A и B используется, чтобы идентифицировать параметры с линейными комбинациями фиксированных и случайных эффектов:
Если матрицы проекта отличаются среди групп, модель становится
Если матрицы проекта также отличаются среди наблюдений, модель становится
Некоторые специфичные для группы предикторы в x i j не могут изменить с наблюдением j. Вызывая тех v i, модель становится
Предположим, что данные для нелинейной модели регрессии попадают в один из m отличные группы i = 1..., m. (А именно, предположите, что группы не вкладываются.), Чтобы задать общую нелинейную модель смешанных эффектов для этих данных:
Задайте специфичные для группы параметры модели φ i как линейные комбинации фиксированных эффектов β и случайные эффекты b i.
Задайте значения ответа y i как нелинейный функциональный f параметров и специфичных для группы переменных прогноза X i.
Модель:
Эта формулировка нелинейной модели смешанных эффектов использует следующее обозначение:
| φ i | Вектор специфичных для группы параметров модели |
| β | Вектор фиксированных эффектов, моделируя параметры генеральной совокупности |
| b i | Вектор многомерных нормально распределенных специфичных для группы случайных эффектов |
| A i | Специфичная для группы матрица проекта для объединения фиксированных эффектов |
| B i | Специфичная для группы матрица проекта для объединения случайных эффектов |
| \Xi | Матрица данных специфичных для группы значений предиктора |
| y i | Вектор данных специфичных для группы значений ответа |
| f | Общая, действительная функция φ i и X i |
| ε i | Вектор специфичных для группы ошибок, принятых, чтобы быть независимым, тождественно, нормально распределенный, и независимый от b i |
| Ψ | Ковариационная матрица для случайных эффектов |
| σ2 | Ошибочное отклонение, принятое, чтобы быть постоянным через наблюдения |
Например, рассмотрите модель устранения препарата от кровотока. Модель включает две перекрывающихся фазы:
p начальной фазы, во время которого концентрации препарата достигают равновесия с окружающими тканями
Вторая фаза q, во время которой препарат устраняется из кровотока
Для данных по нескольким людям i модель
где y i j является наблюдаемой концентрацией в отдельном i во время t i j. Модель позволяет в течение различного времени выборки и различных количеств наблюдений для различных людей.
Уровни устранения r p i и r q i должны быть положительны быть физически значимыми. Осуществите это путем представления логарифмических уровней R p i = журнал (r p i) и R q i = журнал (r q i) и перепараметризации модели:
Выбор, какие параметры к модели со случайными эффектами являются важным соображением при создавании модели смешанных эффектов. Один метод должен добавить случайные эффекты во все параметры и оценки использования их отклонений, чтобы определить их значение в модели. Альтернатива должна соответствовать модели отдельно к каждой группе, без случайных эффектов, и посмотреть на изменение оценок параметра. Если оценка значительно различается через группы, или если доверительные интервалы для каждой группы имеют минимальное перекрытие, параметр является хорошим кандидатом на случайный эффект.
Чтобы ввести зафиксированные эффекты β и случайные эффекты b i для всех параметров модели, повторно выразите модель можно следующим образом:
В обозначении общей модели:
где n i является количеством наблюдений за отдельным i. В этом случае матрицы проекта A i и B i являются, по крайней мере, первоначально, единичными матрицами 4 на 4. Матрицы проекта могут быть изменены, по мере необходимости, чтобы ввести взвешивание отдельных эффектов или зависимость времени.
Подбор кривой модели и оценка ковариационной матрицы Ψ часто приводят к дальнейшим улучшениям. Относительно небольшая оценка для отклонения случайного эффекта предполагает, что это может быть удалено из модели. Аналогично, относительно небольшие оценки для ковариаций среди определенных случайных эффектов предполагает, что полная ковариационная матрица является ненужной. Поскольку случайные эффекты не наблюдаются, Ψ должен быть оценен косвенно. Определение диагонального или диагонального блоком шаблона ковариации для Ψ может улучшить сходимость и эффективность алгоритма подбора.
Функции Statistics and Machine Learning Toolbox™ nlmefit и nlmefitsa соответствуют общей нелинейной модели смешанных эффектов к данным, оценивая фиксированные и случайные эффекты. Функции также оценивают ковариационную матрицу Ψ для случайных эффектов. Дополнительные диагностические выходные параметры позволяют вам оценивать компромиссы между количеством параметров модели и качеством подгонки.
Если модель в Определении Моделей Смешанных Эффектов принимает зависимый группой ковариант, такой как вес (w), модель становится:
Таким образом параметр φ i для любого человека в i th группа:
Чтобы задать ковариационную модель, используйте опцию 'FEGroupDesign'.
'FEGroupDesign' является массивом p-by-q-by-m, задающим различный p-by-q, фиксированные эффекты разрабатывают матрицу для каждой из групп m. Используя предыдущий пример, массив напоминает следующее:
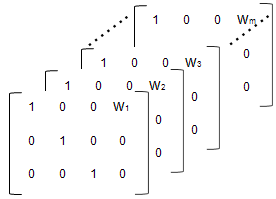
Создайте массив.
% Number of parameters in the model (Phi) num_params = 3; % Number of covariates num_cov = 1; % Assuming number of groups in the data set is 7 num_groups = 7; % Array of covariate values covariates = [75; 52; 66; 55; 70; 58; 62 ]; A = repmat(eye(num_params, num_params+num_cov),... [1,1,num_groups]); A(1,num_params+1,1:num_groups) = covariates(:,1)
Создайте struct с заданной матрицей проекта.
options.FEGroupDesign = A;
Задайте аргументы для nlmefit (или nlmefitsa) как показано в Моделях Смешанных Эффектов Используя nlmefit и nlmefitsa.
Statistics and Machine Learning Toolbox обеспечивает две функции, nlmefit и nlmefitsa для подбора кривой нелинейным моделям смешанных эффектов. Каждая функция предусматривает различные возможности, которые могут помочь вам решить, чтобы использовать.
nlmefit предоставляет следующие четыре метода приближения для подбора кривой нелинейным моделям смешанных эффектов:
'LME' — Используйте вероятность для линейной модели смешанных эффектов в текущих условных оценках beta и B. Это значение по умолчанию.
'RELME' — Используйте ограниченную вероятность для линейной модели смешанных эффектов в текущих условных оценках beta и B.
'FO' — Лапласово приближение первого порядка без случайных эффектов.
'FOCE' — Лапласово приближение первого порядка в условных оценках B.
nlmefitsa предоставляет дополнительный метод приближения, Стохастическая максимизация ожидания приближения (SAEM) [24] с тремя шагами:
Симуляция: Сгенерируйте моделируемые значения случайных эффектов b от следующей плотности p (b |Σ), учитывая текущие оценки параметра.
Стохастическое приближение: Обновите ожидаемое значение логарифмической функции правдоподобия путем принятия ее значение от предыдущего шага и подвижная часть путь к среднему значению логарифмической вероятности, вычисленной от моделируемых случайных эффектов.
Шаг максимизации: Выберите новые оценки параметра, чтобы максимизировать логарифмическую функцию правдоподобия, учитывая моделируемые значения случайных эффектов.
И nlmefit и nlmefitsa пытаются найти, что оценки параметра максимизируют функцию правдоподобия, которую трудно вычислить. nlmefit имеет дело с проблемой путем приближения функции правдоподобия в различных способах и максимизации аппроксимированной функции. Это использует традиционные методы оптимизации, которые зависят от вещей как пределы итерации и критерии сходимости.
nlmefitsa, с другой стороны, моделирует случайные значения параметров таким способом, которым в конечном счете они сходятся к значениям, которые максимизируют точную функцию правдоподобия. Результаты случайны, и традиционные тесты сходимости не применяются. Поэтому nlmefitsa предоставляет возможности строить результаты, в то время как симуляция прогрессирует, и перезапускать симуляцию многократно. Можно использовать эти функции, чтобы судить, сходились ли результаты с точностью, которой вы желаете.
Следующие параметры характерны для nlmefitsa. Большая часть управления стохастический алгоритм.
Cov0 — Начальное значение для ковариационной матрицы PSI. Должен быть r-by-r положительная определенная матрица. Если пустой, значение по умолчанию зависит от значений BETA0.
ComputeStdErrors — true, чтобы вычислить стандартные погрешности для содействующих оценок и сохранить их в структуре вывода STATS или false (значение по умолчанию), чтобы не использовать это вычисление.
LogLikMethod — Задает метод для приближения логарифмической вероятности.
NBurnIn — Количество начальных итераций выжигания дефектов, во время которых не повторно вычисляются оценки параметра. Значение по умолчанию равняется 5.
NIterations — Средства управления, сколько итераций выполняется для каждой из трех фаз алгоритма.
NMCMCIterations — Количество итераций Цепи Маркова Монте-Карло (MCMC).
Существуют некоторые различия в возможностях nlmefit и nlmefitsa. Поэтому некоторые данные и модели применимы с любой функцией, но некоторые могут потребовать, чтобы вы выбрали только одного из них.
Ошибочные модели — nlmefitsa поддерживает множество ошибочных моделей. Например, стандартное отклонение ответа может быть постоянным, пропорциональным значению функции или комбинации двух. nlmefit соответствует моделям под предположением, что стандартное отклонение ответа является постоянным. Одна из ошибочных моделей, 'exponential', указывает, что журнал ответа имеет постоянное стандартное отклонение. Можно соответствовать таким моделям с помощью nlmefit путем обеспечения показаний, как введено, и путем перезаписи образцовой функции, чтобы произвести журнал нелинейного значения функции.
Случайные эффекты — Обе функции соответствуют данным к нелинейной функции с параметрами, и параметры могут быть простыми скалярными значениями или линейными функциями ковариантов. nlmefit позволяет любым коэффициентам линейных функций иметь и зафиксированные и случайные эффекты. nlmefitsa поддерживает случайные эффекты только для константы (прерывание) коэффициент линейных функций, но не для наклонных коэффициентов. Таким образом в примере в Определении Ковариационных Моделей, nlmefitsa может обработать только первые три коэффициента бета как случайные эффекты.
Образцовая форма — nlmefit поддерживает очень общую образцовую спецификацию с немногими ограничениями на матрицы проекта, которые связывают фиксированные коэффициенты и случайные эффекты к параметрам модели. nlmefitsa более строг:
Фиксированный проект эффекта должен быть постоянным в каждой группе (для каждого человека), таким образом, зависимый наблюдением проект не поддержан.
Случайный проект эффекта должен быть постоянным для целого набора данных, таким образом, ни зависимый наблюдением проект, ни зависимый группой проект не поддерживаются.
Как упомянуто под Случайными Эффектами, случайный проект эффекта не должен задавать случайные эффекты для наклонных коэффициентов. Это подразумевает, что проект должен состоять из нулей и единиц.
Случайный проект эффекта не должен использовать тот же случайный эффект для нескольких коэффициентов и не может использовать больше чем один случайный эффект ни для какого одного коэффициента.
Фиксированный проект эффекта не должен использовать тот же коэффициент для нескольких параметров. Это подразумевает, что может иметь самое большее одно ненулевое значение в каждом столбце.
Если вы хотите использовать nlmefitsa для данных, в которых ковариационные эффекты случайны, включают коварианты непосредственно в нелинейное образцовое выражение. Не включайте коварианты в фиксированные или случайные матрицы проекта эффекта.
Сходимость — Как описано в Образцовой форме, nlmefit и nlmefitsa имеет разные подходы к измеряющейся сходимости. nlmefit использует традиционные меры по оптимизации, и nlmefitsa обеспечивает диагностику, чтобы помочь вам судить сходимость случайной симуляции.
На практике nlmefitsa имеет тенденцию быть более устойчивым, и менее вероятно перестать работать на трудных проблемах. Однако nlmefit может сходиться быстрее на проблемах, где он сходится вообще. Некоторые проблемы могут извлечь выгоду из объединенной стратегии, например, путем выполнения nlmefitsa некоторое время, чтобы получить разумные оценки параметра и использования тех в качестве отправной точки для дополнительных итераций с помощью nlmefit.
Поле Outputfcn структуры options задает одну или несколько функций что вызовы решателя после каждой итерации. Как правило, вы можете использовать выходную функцию, чтобы построить точки в каждой итерации или отобразить количества оптимизации из алгоритма. Настраивать выходную функцию:
Запишите выходную функцию как функцию файла MATLAB® или локальную функцию.
Используйте statset, чтобы установить значение Outputfcn, чтобы быть указателем на функцию, то есть, имя функции, которому предшествует знак @. Например, если выходной функцией является outfun.m, команда
options = statset('OutputFcn', @outfun);задает OutputFcn, чтобы быть указателем на outfun. Чтобы задать несколько выходных функций, используйте синтаксис:
options = statset('OutputFcn',{@outfun, @outfun2});Вызовите функцию оптимизации с options как входной параметр.
Для примера выходной функции смотрите Демонстрационную Выходную функцию.
Функциональная строка определения выходной функции имеет следующую форму:
stop = outfun(beta,status,state)
бета является текущими фиксированными эффектами.
состояние является структурой, содержащей данные из текущей итерации. Поля в состоянии описывают структуру подробно.
состояние является текущим состоянием алгоритма. Состояния Алгоритма перечисляют возможные значения.
остановка является флагом, который является true или false в зависимости от того, должна ли стандартная программа оптимизации выйти или продолжиться. Смотрите Флаг Остановки для получения дополнительной информации.
Решатель передает значения входных параметров к outfun в каждой итерации.
В следующей таблице перечислены поля структуры status:
| Поле | Описание |
|---|---|
procedure |
|
iteration | Целое число, запускающееся от 0. |
inner |
Структура, описывающая состояние внутренних итераций в
|
fval | Текущая логарифмическая вероятность |
Psi | Текущая ковариационная матрица случайных эффектов |
theta | Текущая параметризация Psi |
mse | Текущее ошибочное отклонение |
В следующей таблице перечислены возможные значения для state:
| состояние | Описание |
|---|---|
| Алгоритм находится в начальном состоянии перед первой итерацией. |
| Алгоритм в конце итерации. |
| Алгоритм находится в конечном состоянии после последней итерации. |
Следующий код иллюстрирует, как выходная функция может использовать значение state, чтобы решить который задачи выполнить в текущей итерации:
switch state
case 'iter'
% Make updates to plot or guis as needed
case 'init'
% Setup for plots or guis
case 'done'
% Cleanup of plots, guis, or final plot
otherwise
endstop выходного аргумента является флагом, который является true или false. Флаг говорит решатель, должно ли это выйти или продолжиться. Следующие примеры показывают типичные способы использовать флаг stop.
Остановка Оптимизации На основе Промежуточных Результатов. Выходная функция может остановиться, оценка в любой итерации на основе значений аргументов передала в нее. Например, следующая остановка кодовых наборов к истине на основе значения логарифмической вероятности сохранила в поле 'fval' структуры состояния:
stop = outfun(beta,status,state)
stop = false;
% Check if loglikelihood is more than 132.
if status.fval > -132
stop = true;
endОстановка Итерации На основе Входа графический интерфейса пользователя. Если вы разрабатываете графический интерфейс пользователя, чтобы выполнить итерации nlmefit, можно заставить выходную функцию остановиться, когда пользователь нажимает кнопку Stop на графический интерфейсе пользователя. Например, следующий код реализует диалоговое окно, чтобы отменить вычисления:
function retval = stop_outfcn(beta,str,status)
persistent h stop;
if isequal(str.inner.state,'none')
switch(status)
case 'init'
% Initialize dialog
stop = false;
h = msgbox('Press STOP to cancel calculations.',...
'NLMEFIT: Iteration 0 ');
button = findobj(h,'type','uicontrol');
set(button,'String','STOP','Callback',@stopper)
pos = get(h,'Position');
pos(3) = 1.1 * pos(3);
set(h,'Position',pos)
drawnow
case 'iter'
% Display iteration number in the dialog title
set(h,'Name',sprintf('NLMEFIT: Iteration %d',...
str.iteration))
drawnow;
case 'done'
% Delete dialog
delete(h);
end
end
if stop
% Stop if the dialog button has been pressed
delete(h)
end
retval = stop;
function stopper(varargin)
% Set flag to stop when button is pressed
stop = true;
disp('Calculation stopped.')
end
end
nmlefitoutputfcn является демонстрационной выходной функцией Statistics and Machine Learning Toolbox для nlmefit и nlmefitsa. Это инициализирует или обновляет график с фиксированными эффектами (BETA) и отклонение случайных эффектов (diag (STATUS.Psi)). Для nlmefit график также включает логарифмическую вероятность (STATUS.fval).
nlmefitoutputfcn является выходной функцией по умолчанию для nlmefitsa. Чтобы использовать его с nlmefit, задайте указатель на функцию для него в структуре опций:
opt = statset('OutputFcn', @nlmefitoutputfcn, …)
beta = nlmefit(…, 'Options', opt, …), чтобы nlmefitsa использовал этой функции, задайте пустое значение для выходной функции:opt = statset('OutputFcn', [], …)
beta = nlmefitsa(…, 'Options', opt, …)nlmefitoutputfcn останавливает nlmefit или nlmefitsa, если вы закрываете фигуру, которую это производит.