Выполните неклассическое многомерное масштабирование с помощью mdscale.
Функциональный mdscale выполняет неклассическое многомерное масштабирование. Как с cmdscale, вы используете mdscale или чтобы визуализировать данные о несходстве, для которых никакие “местоположения” не существуют, или визуализировать высоко-размерные данные путем сокращения его размерности. Обе функции берут матрицу несходств как вход и производят настройку точек. Однако mdscale предлагает выбор различных критериев создать настройку и позволяет недостающие данные и веса.
Например, зерновые данные включают измерения на 10 переменных, описывающих блюда из хлопьев для завтрака. Можно использовать mdscale, чтобы визуализировать эти данные в двух измерениях. Во-первых, загрузите данные. Для ясности этот пример кода выбирает подмножество 22 из наблюдений.
load cereal.mat
X = [Calories Protein Fat Sodium Fiber ...
Carbo Sugars Shelf Potass Vitamins];
% Take a subset from a single manufacturer
mfg1 = strcmp('G',cellstr(Mfg));
X = X(mfg1,:);
size(X)
ans =
22 10Затем используйте pdist, чтобы преобразовать 10-мерные данные в несходства. Вывод от pdist является симметричной матрицей несходства, сохраненной как вектор, содержащий только (23*22/2) элементы в его верхнем треугольнике.
dissimilarities = pdist(zscore(X),'cityblock');
size(dissimilarities)
ans =
1 231Этот пример кода сначала стандартизирует зерновые данные, и затем использует расстояние городского квартала в качестве несходства. Выбор преобразования к несходствам является зависящим от приложения, и выбор здесь только для простоты. В некоторых приложениях исходные данные уже в форме несходств.
Затем, используйте mdscale, чтобы выполнить метрический MDS. В отличие от cmdscale, необходимо задать желаемое количество размерностей и метод, чтобы использовать, чтобы создать выходную настройку. В данном примере используйте две размерности. Метрический критерий STRESS является общепринятой методикой для вычисления вывода; для другого выбора смотрите страницу с описанием mdscale в онлайн-документации. Второй вывод от mdscale является значением того критерия, оцененного для выходной настройки. Это измеряется, как хорошо разделять знаками препинания расстояния выходной настройки аппроксимируют исходные входные несходства:
[Y,stress] =...
mdscale(dissimilarities,2,'criterion','metricstress');
stress
stress =
0.1856scatterplot вывода от mdscale представляет исходные 10-мерные данные в двух измерениях, и можно использовать функцию gname, чтобы маркировать выбранные точки:
plot(Y(:,1),Y(:,2),'o','LineWidth',2); gname(Name(mfg1))
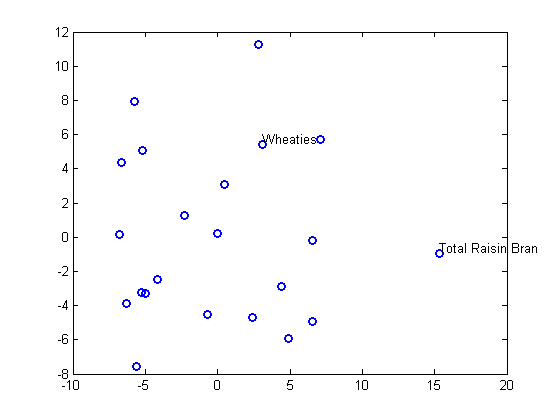
Метрическое многомерное масштабирование создает настройку точек, чьи разделяют знаками препинания расстояния, аппроксимированные данные несходства. Это иногда - слишком строгое требование, и неметрическое масштабирование разработано, чтобы ослабить его немного. Вместо того, чтобы пытаться аппроксимировать сами несходства, неметрическое масштабирование аппроксимирует нелинейное, но монотонное, преобразование их. Из-за монотонности большие или меньшие расстояния на графике вывода будут соответствовать большим или меньшим несходствам, соответственно. Однако нелинейность подразумевает, что mdscale только пытается сохранить упорядоченное расположение несходств. Таким образом могут быть сокращения или расширения расстояний в различных шкалах.
Вы используете mdscale, чтобы выполнить неметрический MDS почти таким же способом что касается метрического масштабирования. Неметрический критерий STRESS является общепринятой методикой для вычисления вывода; для большего количества вариантов смотрите страницу с описанием mdscale в онлайн-документации. Как с метрическим масштабированием, второй вывод от mdscale является значением того критерия, оцененного для выходной настройки. Для неметрического масштабирования, однако, это измеряется, как хорошо разделять знаками препинания расстояния выходной настройки аппроксимируют несоизмеримости. Несоизмеримости возвращены в третьем выводе. Они - преобразованные значения исходных несходств:
[Y,stress,disparities] = ...
mdscale(dissimilarities,2,'criterion','stress');
stress
stress =
0.1562Чтобы проверять припадок выходной настройки к несходствам и понять несоизмеримости, это помогает сделать график Шепарда:
distances = pdist(Y);
[dum,ord] = sortrows([disparities(:) dissimilarities(:)]);
plot(dissimilarities,distances,'bo', ...
dissimilarities(ord),disparities(ord),'r.-', ...
[0 25],[0 25],'k-')
xlabel('Dissimilarities')
ylabel('Distances/Disparities')
legend({'Distances' 'Disparities' '1:1 Line'},...
'Location','NorthWest');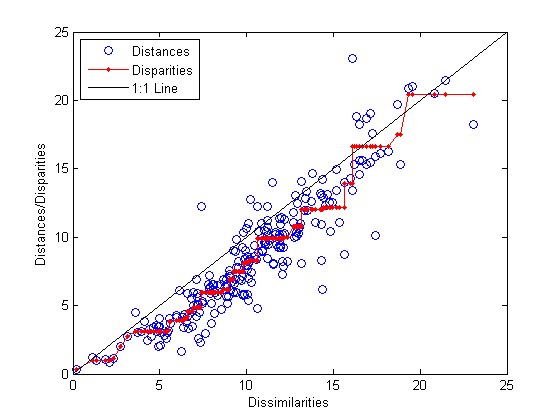
Этот график показывает, что mdscale нашел настройку точек в двух измерениях, чьи разделяют расстояния знаками препинания, аппроксимирует несоизмеримости, которые в свою очередь являются нелинейным преобразованием исходных несходств. Вогнутая форма несоизмеримостей как функция несходств указывает, что подгонка имеет тенденцию сокращать маленькие расстояния относительно соответствующих несходств. Это может быть совершенно приемлемо на практике.
mdscale использует итеративный алгоритм, чтобы найти выходную настройку, и результаты могут часто зависеть от отправной точки. По умолчанию mdscale использует cmdscale, чтобы создать начальную настройку, и этот выбор часто приводит к глобально лучшему решению. Однако для mdscale возможно остановиться в настройке, которая является локальным минимумом критерия. Такие случаи могут быть диагностированы и часто преодолеваться путем выполнения mdscale многократно с различными отправными точками. Можно сделать это использование аргументов пары "имя-значение" 'start' и 'replicates'. Следующий код запускается пять, реплицирует MDS, каждый запускающийся в различной случайным образом выбранной начальной настройке. Значение критерия распечатывается для каждой репликации; mdscale возвращает настройку с лучшей подгонкой.
opts = statset('Display','final');
[Y,stress] =...
mdscale(dissimilarities,2,'criterion','stress',...
'start','random','replicates',5,'Options',opts);
35 iterations, Final stress criterion = 0.156209
31 iterations, Final stress criterion = 0.156209
48 iterations, Final stress criterion = 0.171209
33 iterations, Final stress criterion = 0.175341
32 iterations, Final stress criterion = 0.185881Заметьте, что mdscale находит несколько различных локальных решений, некоторые из которых не имеют столь низкого значения напряжений, как решение нашло с отправной точкой cmdscale.