`ellipticPi`

Полные и неполные эллиптические интегралы третьего вида

Блокноты MuPAD® будут демонтированы в будущем релизе. Используйте live скрипты MATLAB® вместо этого.

Live скрипты MATLAB поддерживают большую часть функциональности MuPAD, хотя существуют некоторые различия. Для получения дополнительной информации смотрите, Преобразовывают Notebook MuPAD в Live скрипты MATLAB.

Синтаксис

ellipticPi(n,<φ>,m)

Описание

ellipticPi(n,m) представляет полный эллиптический интеграл третьего вида

$Π (n, m) = Π (n; \frac{π}{2} | m) = \int_{0}^{π / 2} \frac{1}{(1 - n \sin^{2} θ) \sqrt{1 - m \sin^{2} θ}} d θ$

ellipticPi(n,φ,m) представляет неполный эллиптический интеграл третьего вида

$Π (n, m) = Π (n; φ | m) = \int_{0}^{φ} \frac{1}{(1 - n \sin^{2} θ) \sqrt{1 - m \sin^{2} θ}} d θ$

Эллиптические интегралы третьего вида заданы для сложных аргументов m, ϕ и n.

Если все аргументы являются числовыми, и по крайней мере один - значение с плавающей точкой, ellipticPi(n,<φ>,m) возвращает результаты с плавающей точкой. Для большинства точных аргументов это отвечает на неоцененные символьные звонки. Можно аппроксимировать такие результаты с числами с плавающей запятой с помощью функции float.

Взаимодействия среды

Когда названо аргументами с плавающей точкой, эта функция чувствительна к переменной окружения DIGITS, который определяет числовую рабочую точность.

Примеры

Пример 1

Большинство вызовов с точными аргументами возвращает себя неоцененный. Чтобы аппроксимировать такие значения с числами с плавающей запятой, используйте float:

ellipticPi(PI/4, I);
float(ellipticPi(PI/4, I))

Также используйте значение с плавающей точкой в качестве аргумента:

ellipticPi(1/2, 1, 1/4);
ellipticPi(0.5, 1, 1/4)

Некоторые специальные аргументы возвращают явные символьные представления:

ellipticPi(n, 0);
ellipticPi(0, m);
ellipticPi(0, p, m);
ellipticPi(1, p, m)

Параметры

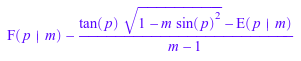
`m`	Арифметическое выражение, задающее параметр.
φ	Арифметическое выражение, задающее амплитуду. Значение по умолчанию $\frac{π}{2}$ .
`n`	Арифметическое выражение, задающее характеристику.

Возвращаемые значения

Арифметическое выражение.

Смотрите также

Функции MuPAD

ellipticCE | ellipticCK | ellipticCPi | ellipticE | ellipticF | ellipticK

Документация Symbolic Math Toolbox

Поддержка

Памятка переводчика

1. Если смысл перевода понятен, то лучше оставьте как есть и не придирайтесь к словам, синонимам и тому подобному. О вкусах не спорим.

2. Не дополняйте перевод комментариями “от себя”. В исправлении не должно появляться дополнительных смыслов и комментариев, отсутствующих в оригинале. Такие правки не получится интегрировать в алгоритме автоматического перевода.

3. Сохраняйте структуру оригинального текста - например, не разбивайте одно предложение на два.

4. Не имеет смысла однотипное исправление перевода какого-то термина во всех предложениях. Исправляйте только в одном месте. Когда Вашу правку одобрят, это исправление будет алгоритмически распространено и на другие части документации.

5. По иным вопросам, например если надо исправить заблокированное для перевода слово, обратитесь к редакторам через форму технической поддержки.