IntMethodМетод для интегрального приближения
Блокноты MuPAD® будут демонтированы в будущем релизе. Используйте live скрипты MATLAB® вместо этого.
Live скрипты MATLAB поддерживают большую часть функциональности MuPAD, хотя существуют некоторые различия. Для получения дополнительной информации смотрите, Преобразовывают Notebook MuPAD в Live скрипты MATLAB.
| Дополнительный | Exact, RiemannLeft, RiemannRight, RiemannLower, RiemannUpper, RiemannMiddle, RiemannLowerAbs, RiemannUpperAbs, Simpson или Trapezoid |
| Объекты | Значения по умолчанию IntMethod |
|---|---|
plot::Integral | Exact |
IntMethod определяет метод визуализации объектов plot::Integral.
Реализованы следующие методы:
Точный
область между осью X и функциональным графиком окрашена
RiemannLower
отобразите поля между осью X и функциональным графиком с помощью наименьшего значения функции в каждом подынтервале
RiemannLowerAbs
отобразите поля между осью X и функциональным графиком с помощью наименьшего абсолютного значения функции в каждом подынтервале
RiemannUpper
отобразите поля между осью X и функциональным графиком с помощью самого большого значения функции в каждом подынтервале
RiemannUpperAbs
отобразите поля между осью X и функциональным графиком с помощью самого большого абсолютного значения функции в каждом подынтервале
RiemannLeft
отобразите поля между осью X и функциональным графиком с помощью значения функции левой границы в каждом подынтервале
RiemannMiddle
отобразите поля между осью X и функциональным графиком с помощью значения функции середины в каждом подынтервале
RiemannRight
отобразите поля между осью X и функциональным графиком с помощью значения функции правильной границы в каждом подынтервале
Трапецоид
отобразите приближение интеграла с помощью Метода трапеций
Симпсон
интерполируйте график функции, использующей правило Симпсонов
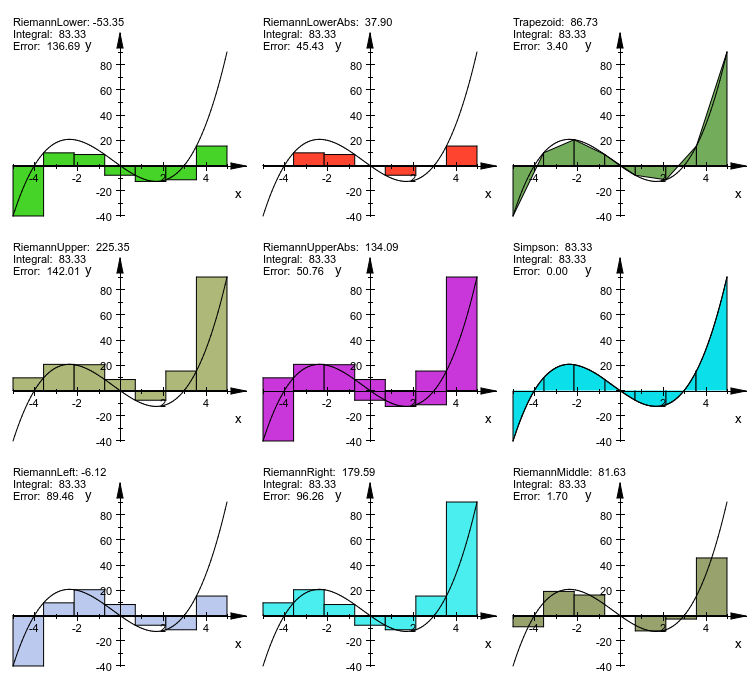
Следующий пример показывает все реализованные методы:
f := plot::Function2d(x*(x-3)*(x+4), Color = RGB::Black):
plot(plot::Scene2d(plot::Integral(f, 7, IntMethod = method,
Color = [frandom() $ i=1..3],
ShowInfo = [IntMethod, Integral,
Error, Position = [-5,90]]), f)
$ method in [RiemannLower, RiemannLowerAbs, Trapezoid,
RiemannUpper, RiemannUpperAbs, Simpson,
RiemannLeft, RiemannRight, RiemannMiddle],
Columns = 3, TextFont = [8], Width = 200, Height = 180)