график::Числовое приближение интеграла
Блокноты MuPAD® будут демонтированы в будущем релизе. Используйте live скрипты MATLAB® вместо этого.
Live скрипты MATLAB поддерживают большую часть функциональности MuPAD, хотя существуют некоторые различия. Для получения дополнительной информации смотрите, Преобразовывают Notebook MuPAD в Live скрипты MATLAB.
plot::Integral(f, <n>, <IntMethod = m>, <a = amin .. amax>, options)
plot::Integral(f, IntMethod = m) визуализирует приближение интеграла функционального f с помощью числового квадратурного метода m. Суммы Римана, метод трапеций и правило Симпсона доступны.
plot::Integral(f, n, IntMethod = m) использует подынтервалы n, чтобы аппроксимировать интеграл.
Атрибут IntMethod определяет численный метод. Суммы Римана, метод трапеций или правило Симпсона доступны. Смотрите страницу справки IntMethod для получения дальнейшей информации. Cf. Пример 1.
plot::Integral не строит функциональный график подынтегрального выражения. Если подынтегральное выражение должно быть построено также, f должен быть передан команде plot вместе с объектом приближения типа plot::Integral.
Если никакой квадратурный метод не задан IntMethod = m, plot::Integral только штрихует область между функциональным f и осью X.
Несколько объектов plot::Integral могут быть построены вместе, чтобы проиллюстрировать различие между различными квадратурными методами. Порядок объектов в команде plot определяет объект впереди.
График содержит информацию о предоставляющем текстового объекта о квадратурном методе, значении приближения, точном значении интеграла, квадратурной ошибки и количества узлов. Смотрите страницу справки атрибута ShowInfo для получения дальнейшей информации.
| Атрибут | Цель | Значение по умолчанию |
|---|---|---|
AffectViewingBox | влияние объектов на ViewingBox сцены | TRUE |
AntiAliased | сглаженные строки и точки? | TRUE |
Color | основной цвет | RGB::PaleBlue |
Filled | заполненные или прозрачные области и поверхности | TRUE |
FillColor | цвет областей и поверхностей | RGB::PaleBlue |
FillPattern | тип заполнения области | Solid |
Frames | количество кадров в анимации | 50 |
Function1 | первая штриховка разграничивания функции/кривой | |
HorizontalAlignment | выравнивание по горизонтали текстовых объектов w.r.t. их координаты | Left |
IntMethod | метод для интегрального приближения | Exact |
Legend | делает запись легенды | |
LegendText | короткий объяснительный текст для легенды | |
LegendEntry | добавить этот объект в легенду? | FALSE |
LineColor | цвет строк | RGB::Black |
LineWidth | ширина строк | 0.35 |
LineColor2 | цвет строк | RGB::Grey |
LineStyle | тело, подчеркнутые штриховой линией или пунктирные линии? | Solid |
LinesVisible | видимость строк | TRUE |
LineColorType | типы окраски строки | Flat |
LineColorFunction | функциональная окраска строки | |
Name | имя объекта графика (для браузера и легенды) | |
Nodes | количество подынтервалов или список x-значений для подынтервалов | [10] |
ParameterEnd | закончите значение параметра анимации | |
ParameterName | имя параметра анимации | |
ParameterBegin | начальное значение параметра анимации | |
ParameterRange | область значений параметра анимации | |
PointSize | размер точек | 1.5 |
PointStyle | стиль презентации точек | FilledCircles |
PointsVisible | видимость точек mesh | FALSE |
ShowInfo | Информация об интегральном приближении | [2, IntMethod, Integral] |
TextFont | шрифт текстовых объектов | [" sans-serif ", 11] |
TextRotation | вращение 2D текста | 0 |
TimeEnd | время окончания анимации | 10.0 |
TimeBegin | время начала анимации | 0.0 |
TimeRange | оперативный промежуток анимации | 0.0 .. 10.0 |
Title | объектный заголовок | |
TitleFont | шрифт объектных заголовков | [" sans-serif ", 11] |
TitlePosition | положение объектных заголовков | |
TitleAlignment | выравнивание по горизонтали заголовков w.r.t. их координаты | Center |
TitlePositionX | положение объектных заголовков, x компонент | |
TitlePositionY | положение объектных заголовков, y компонент | |
VerticalAlignment | выравнивание по вертикали текстовых объектов w.r.t. их координаты | Bottom |
Visible | видимость | TRUE |
VisibleAfter | объект, видимый после этой временной стоимости | |
VisibleBefore | объект, видимый до этой временной стоимости | |
VisibleFromTo | объект, видимый в это время, располагается | |
VisibleAfterEnd | объект, видимый после его законченного времени анимации? | TRUE |
VisibleBeforeBegin | объект, видимый перед его временем анимации, запускается? | TRUE |
Если один объект plot::Function2d дан, не задавая метод приближения, plot::Integral только штрихует область между функциональным графиком и осью X:
f := plot::Function2d(cos(x), x = -PI..PI): plot(plot::Integral(f), f)
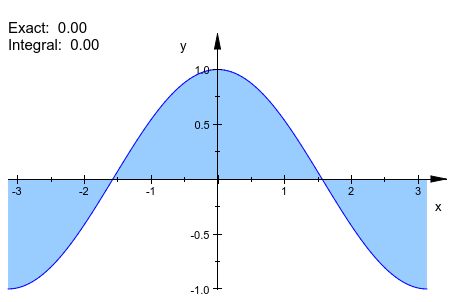
Обратите внимание на то, что plot::Integral требует объекта типа plot::Function2d, не только выражение function:
plot::Integral(sin(x))
Error: First argument must be a 'plot::Function2d' object. [plot::Integral::new]
Если метод приближения задан, числовое квадратурное значение, вычисленное этим методом, отображено:
plot(plot::Integral(f, IntMethod = RiemannLower))
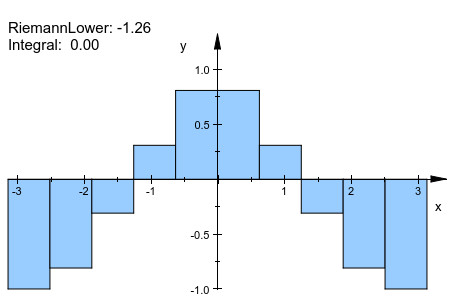
Номер квадратурных интервалов может быть определен путем передачи второго аргумента n или путем определения Nodes = n:
plot(plot::Integral(f, 20, IntMethod = RiemannLower))
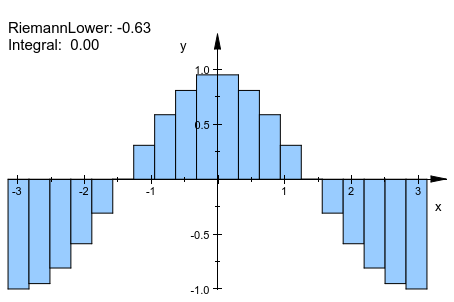
Чтобы видеть подынтегральное выражение в графике, функциональный объект должен быть передан вместе с объектом приближения. Порядок определяет, который объект впереди:
plot(plot::Integral(f, IntMethod = RiemannLower), f)
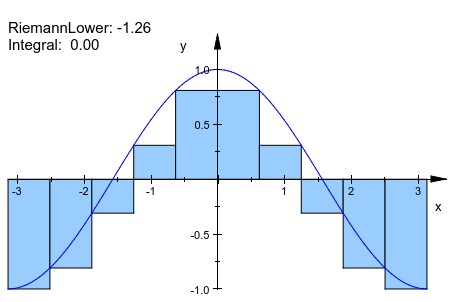
delete f:
Отображенная информация может быть сконфигурирована пользователем:
f := plot::Function2d(x^2, x = -5..5, Color = RGB::DarkGrey):
plot(plot::Integral(f, IntMethod = RiemannLower,
ShowInfo = [1, IntMethod = "Riemann lower sum",
Integral = "Exact value",
2, Error = "Difference"]), f)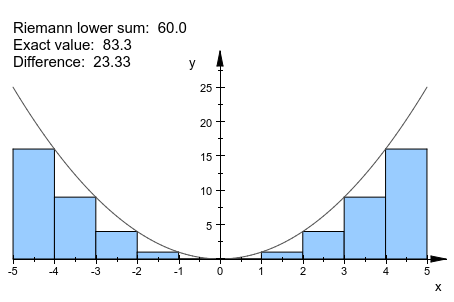
delete f:
Можно объединить несколько объектов приближения, например, ниже и верхняя сумма:
f := plot::Function2d(x^2, x = -5..5):
plot(plot::Integral(f, IntMethod = RiemannUpper,
Color = RGB::Blue),
plot::Integral(f, IntMethod = RiemannLower,
Color = RGB::LightYellow),
f)
Автоматически помещенное информационное текстовое перекрытие. Чтобы исправить это, опция, ShowInfo должен использоваться. В тексте верхней суммы вставляется одна дополнительная пустая строка. Кроме этого, оба объекта используют значение по умолчанию, поэтому нет потребности задать ShowInfo во втором объекте:
plot(plot::Integral(f, IntMethod = RiemannUpper,
ShowInfo = [IntMethod, "", Integral]),
plot::Integral(f, IntMethod = RiemannLower,
Color = RGB::LightYellow),
f)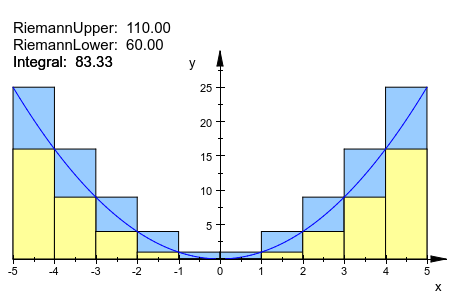
Информационный текст может быть расположен явным образом:
plot(plot::Integral(f, IntMethod = RiemannUpper,
ShowInfo = [IntMethod, Integral,
Position = [-5, -1]],
VerticalAlignment = Top),
plot::Integral(f, IntMethod = RiemannLower, Color = RGB::Yellow,
ShowInfo = [IntMethod,
Position = [0, -1]],
VerticalAlignment = Top),
f)
delete f:
plot::Integral может быть анимирован:
f := plot::Function2d(sin(a*x), x = 0..PI, a = 1..5): plot(plot::Integral(f, 50, IntMethod = RiemannMiddle), f)
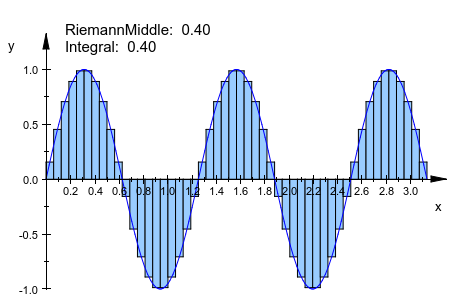
Увеличение числа узлов уменьшает квадратурную ошибку:
f := plot::Function2d(sin(x), x = 0..PI): plot(plot::Integral(f, N, N = 10..50, IntMethod = RiemannLower), f)
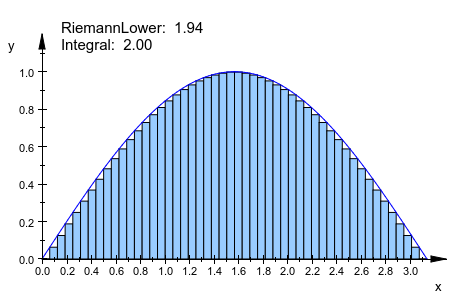
Функция и количество узлов могут быть анимированы одновременно:
f := plot::Function2d(sin(a*x), x = 0..PI, a = 1..5): plot(plot::Integral(f, N, N = 10..50, IntMethod = RiemannLower), f)
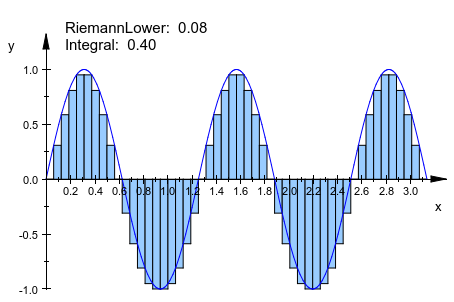
delete f:
|
Подынтегральное выражение: объект типа
|
|
Количество подынтервалов (положительное целое число) или список вещественных чисел, представляющих узлы переменной интегрирования.
|
|
Параметр анимации, заданный как |
|
Опция, заданная как Квадратурный метод; смотрите |