ode:: unimodularПреобразование Unimodular линейного обыкновенного дифференциального уравнения
Блокноты MuPAD® будут демонтированы в будущем релизе. Используйте live скрипты MATLAB® вместо этого.
Live скрипты MATLAB поддерживают большую часть функциональности MuPAD, хотя существуют некоторые различия. Для получения дополнительной информации смотрите, Преобразовывают Notebook MuPAD в Live скрипты MATLAB.
ode::unimodular(Ly, y(x), <Transform>)
ode::unimodular(Ly, y(x)) тестирует, если линейное гомогенное дифференциальное уравнение, Ly имеет unimodular группу Галуа (т.е. Вронскиан находится в основном поле ℚ (x)), если не преобразовывает Ly в unimodular один (путем изменения второго по высоте коэффициента, чтобы обнулить) и возвращает table с индексом equation и factorOfTransformation, содержащий соответственно преобразованное дифференциальное уравнение и фактор преобразования Wn, таким образом, что решение преобразованного уравнения, умноженного на Wn, является решением Ly.
Если опция, Transform дан затем Ly, преобразовывается безусловно, даже если Ly имеет уже unimodular группу Галуа.
Мы тестируем, если следующее дифференциальное уравнение имеет unimodular группу Галуа:
Ly := y(x)*6+x*diff(y(x),x)*(-2)+diff(y(x),x$2)*(-x^2+1)
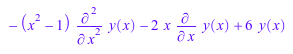
ode::unimodular(Ly, y(x))
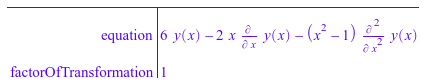
Это - unimodular, поскольку фактором преобразования является 1. Мы можем также проверять это путем вычисления Вронскиана Ly, который является рациональной функцией:
ode::wronskian(Ly,y(x))
![]()
Теперь мы преобразовываем Ly в дифференциальное уравнение, Вронскианом которого является 1:
ode::unimodular(Ly, y(x), Transform)

ode::wronskian(%[equation], y(x))
![]()
|
Гомогенное линейное дифференциальное уравнение по ℚ (x). |
|
Зависимая функция |