sqrtФункция квадратного корня
Блокноты MuPAD® будут демонтированы в будущем релизе. Используйте live скрипты MATLAB® вместо этого.
Live скрипты MATLAB поддерживают большую часть функциональности MuPAD, хотя существуют некоторые различия. Для получения дополнительной информации смотрите, Преобразовывают Notebook MuPAD в Live скрипты MATLAB.
sqrt(z)
sqrt(z) представляет квадратный корень из z.
представляет решение x 2 = z, который имеет неотрицательную действительную часть. В частности, это представляет положительный корень для действительного положительного z. Для действительного отрицательного z это представляет комплексный корень с положительной мнимой частью.
Результат с плавающей точкой возвращен для аргументов с плавающей точкой. Обратите внимание на то, что разрез выбран в качестве отрицательной действительной полуоси. Значения, возвращенные sqrt, переходят при пересечении этого сокращения. Cf. Пример 2.
Могут произойти определенные упрощения аргумента. В частности, положительные целочисленные факторы извлечены от некоторых символьных продуктов. Cf. Пример 3.
Обратите внимание на то, что
не может быть упрощен до x для всех комплексных чисел (например,
для действительного x <0). Cf. Пример 4.
Математически, sqrt(z) совпадает с z^(1/2) = _power(z,1/2). Однако sqrt обеспечивает больше упрощений, чем _power. Cf. Пример 5.
Когда названо аргументом с плавающей точкой, функция чувствительна к переменной окружения DIGITS, который определяет числовую рабочую точность.
Мы демонстрируем некоторые вызовы с точными и символьными входными данными:
sqrt(2), sqrt(4), sqrt(36*7), sqrt(127)
sqrt(1/4), sqrt(1/2), sqrt(3/4), sqrt(25/36/7), sqrt(4/127)
sqrt(-4), sqrt(-1/2), sqrt(1 + I)
sqrt(x), sqrt(4*x^(4/7)), sqrt(4*x/3), sqrt(4*(x + I))
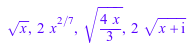
Значения с плавающей точкой вычисляются для аргументов с плавающей точкой:
sqrt(1234.5), sqrt(-1234.5), sqrt(-2.0 + 3.0*I)
Скачок происходит при пересечении отрицательной действительной полу оси:
sqrt(-4.0), sqrt(-4.0 + I/10^100), sqrt(-4.0 - I/10^100)
Квадратный корень из символьных продуктов, включающих положительные целочисленные факторы, упрощен:
sqrt(20*x*y*z)
Квадратные корни из квадратов не упрощены, если аргумент не действителен, и его знак известен:
sqrt(x^2*y^4)
assume(x > 0): sqrt(x^2*y^4)
assume(x < 0): sqrt(x^2*y^4)
sqrt обеспечивает больше упрощений, чем функция _power:
sqrt(4*x), (4*x)^(1/2) = _power(4*x, 1/2)
|
Арифметическое выражение.
z