zetaДзета-функция Римана
Блокноты MuPAD® будут демонтированы в будущем релизе. Используйте live скрипты MATLAB® вместо этого.
Live скрипты MATLAB поддерживают большую часть функциональности MuPAD, хотя существуют некоторые различия. Для получения дополнительной информации смотрите, Преобразовывают Notebook MuPAD в Live скрипты MATLAB.
zeta(z) zeta(z,n)
zeta(z) представляет Дзета-функцию Римана
.
zeta(z, n) представляет энную производную
дзета-функции.
Ряды сходятся, только если действительная часть z больше, чем 1. Определение дзета-функции расширено к целой комплексной плоскости, за исключением простого полюса z = 1, аналитическим продолжением.
Вызовы zeta(z) и zeta(z, 0) эквивалентны.
Результат с плавающей точкой возвращен для аргументов z с плавающей точкой.
Следующие специальные точные значения реализованы:
, 
,
ζ (z) = 0 для даже целых чисел z <0,
для нечетных целых чисел удовлетворение z - Pref:: autoExpansionLimit () ≤ z <0,
для даже целых чисел z, удовлетворяющий 0 ≤ z ≤ Pref:: autoExpansionLimit (),
ζ (∞) = 1, ζ (∞, n) = 0 для n> 0.
zeta возвращает символьный вызов функции, если аргумент не оценивает к одному из вышеупомянутых чисел.
Оценка с плавающей точкой является довольно медленной для больших значений n. Далее, для большого n, оценка для ℜ (z) <0 намного медленнее, чем оценка для ℜ (z) ≥ 0.
Когда названо аргументом z с плавающей точкой, функция чувствительна к переменной окружения DIGITS, который определяет числовую рабочую точность.
Мы демонстрируем некоторые вызовы с точными и символьными входными данными:
zeta(-6), zeta(-5), zeta(-4), zeta(-3), zeta(-2), zeta(-1)
zeta(0), zeta(2), zeta(3), zeta(4), zeta(5), zeta(6), zeta(7)
zeta(1/2), zeta(1 + I, 1), zeta(z^2 -I, 2)
Вот некоторые значения производной дзета-функции:
zeta(0, 1), zeta(infinity, 1)
Значения с плавающей точкой вычисляются для аргументов с плавающей точкой:
zeta(-1001.0), zeta(12.3, 1), zeta(0.5 + 14.13472514*I, 2)
zeta имеет полюс в точке z = 1:
zeta(1)
Error: Singularity. [zeta]
Ища нетривиальные корни Дзета-функции, мы строим функциональный f (z) = |ζ (z) | вдоль “критической строки” комплексных чисел с действительной частью
:
plotfunc2d(abs(zeta(1/2 + y*I)), y = 0..30,
Mesh = 500,
AxesTitles = ["y", "|zeta|"])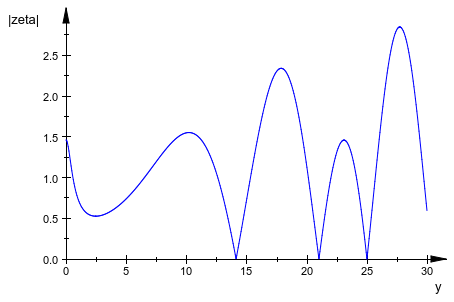
Следующие вызовы ищут числовые корни вдоль критической строки:
numeric::solve(zeta(1/2 + I*y), y = 10..20), numeric::solve(zeta(1/2 + I*y), y = 20..22), numeric::solve(zeta(1/2 + I*y), y = 22..26)
| |
|
Арифметическое выражение, представляющее неотрицательное целое число |
Арифметическое выражение.
z