Документация

Камеры в 3D

Модель графики MuPAD^® 3D включает наблюдателя в определенное положение, указывая камеру с линзой определенного вводного угла к некоторому определенному центру. Определенные параметры “положение”, “угол” и “центр” определяют снимок, который сделает камера.

Когда 3D изображение создается в MuPAD, камера с соответствующей линзой по умолчанию расположена автоматически. Его центр выбран в качестве центра графической сцены. Интерактивное средство просмотра позволяет вращать сцену, которая, на самом деле, реализована внутренне как изменение положения камеры. Также интерактивное увеличивание масштаб и уменьшение масштаб поняты, двигая камеру поближе к или дальше от сцены.

Кроме интерактивных движений камеры, перспектива 3D изображения может также быть установлена в вызовах, генерирующих график. Один путь состоит в том, чтобы задать направление, от которого камера указывает на сцену. Это сделано через атрибут CameraDirection:

plot(plot::Function3d(sin(x + y^3), x = -1..1, y = -1..1),
     CameraDirection = [-25, 20, 30]):

plot(plot::Function3d(sin(x + y^3), x = -1..1, y = -1..1),
     CameraDirection = [10, -40, 10]):

В этих вызовах положение камеры не полностью задано CameraDirection. Этот атрибут только запрашивает камеру быть помещенной в некоторое большое расстояние от сцены вдоль луча в направлении, данном атрибутом. Фактическое расстояние от сцены полно решимости автоматически позволить графической сцене заполнить изображение оптимально.

Для полной спецификации перспективы существуют объекты камеры типа plot::Camera, которые позволяют задавать положение камеры, ее центра и вводного угла ее линзы:

position := [-5, -10, 5]:
focalpoint := [0, 0, 0]:
angle := PI/12:
camera := plot::Camera(position, focalpoint, angle):

Эта камера может быть передана как любой графический объект команде plot, генерирующей сцену. Если объект камеры задан в графической сцене, он определяет представление. Никакая “автоматическая камера” не используется:

plot(plot::Function3d(sin(x + y^3), x = -1..1, y = -1..1),
     camera):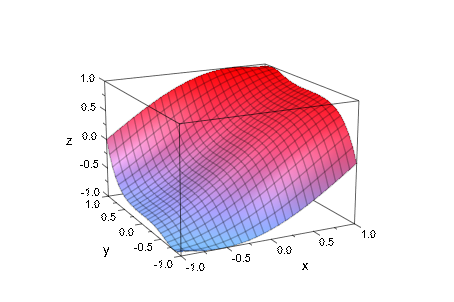

Объекты камеры могут быть анимированы:

camera := plot::Camera([3*cos(a), 3*sin(a), 1 + cos(2*a)],
                       [0, 0, 0], PI/3, a = 0..2*PI, 
                       Frames = 100):

Вставляя анимированную камеру в графическую сцену, мы получаем анимированный график, моделирующий “рейс вокруг сцены”:

plot(plot::Function3d(sin(x + y^3), x = -1..1, y = -1..1),
     camera):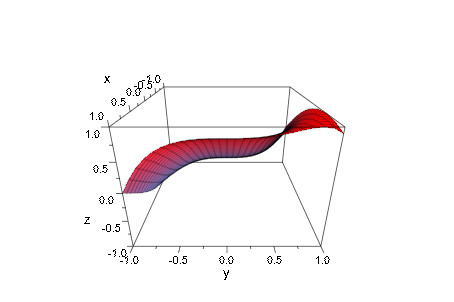

На самом деле несколько камер могут быть установлены одновременно в сцене:

camera1 := plot::Camera([3*cos(a), 3*sin(a), 1 + cos(2*a)],
                        [0, 0, 0], PI/3, a = 0..2*PI,
                        Name = "Camera 1"):
camera2 := plot::Camera([2*cos(a), 2*sin(a), 2 + cos(2*a)],
                        [0, 0, 0], PI/3, a = 0..2*PI,
                        Name = "Camera 2"):
plot(plot::Function3d(sin(x + y^3), x = -1..1, y = -1..1),
     camera1, camera2):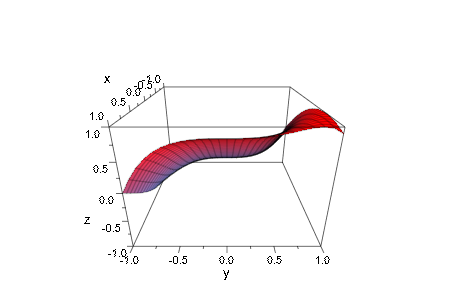

На значение по умолчанию первая камера производит представленное представление. После нажатия на другую камеру в обозревателе объектов средства просмотра (см. раздел Viewer, Браузер и Инспектора: Интерактивная Манипуляция), выбранная камера вступает во владение, и новое представление показывают.

Затем, мы взглянули на более привлекательный пример: так называемый “Аттрактор Лоренца”. ОДУ Лоренца является системой

с фиксированными параметрами p, r, b. Как динамическая система для Y = [x, y, z], мы должны решить ОДУ со следующим векторным полем:

f := proc(t, Y)
     local x, y, z;
     begin
        [x, y, z] := Y:
        [p*(y - x), -x*z + r*x - y, x*y - b*z]
     end_proc:

Считайте следующие параметры и следующее начальное условие Y0:

p := 10: r := 28: b := 1: Y0 := [1, 1, 1]:

Стандартный plot::Ode3d служит для генерации графического 3D решения динамической системы. Это решает ОДУ численно и генерирует графические данные от числовой mesh. Данные о графике заданы пользователем через “генераторы” (процедуры), которые сопоставляют точку решения (t, Y) к точке (x, y, z) в 3D.

Следующий генератор Gxyz производит 3D график фазы решения. Генератор Gyz проектирует кривую решения к (y, z) плоскость с x = - 20; генератор Gxz проектирует кривую решения к (x, z) плоскость с y = - 20; генератор Gxy проектирует кривую решения к (x, y) плоскость с z = 0:

Gxyz := (t, Y) -> Y:
Gyz := (t, Y) -> [-20, Y[2], Y[3]]:
Gxz := (t, Y) -> [Y[1], -20, Y[3]]:
Gxy := (t, Y) -> [Y[1], Y[2], 0]:

С этими генераторами мы создаем 3D объект графика, состоящий из кривой фазы и ее проекций. Следующая команда вызывает числовой решатель numeric::odesolve, чтобы произвести графические данные. Это берет о половине минуты на компьютере на 1 ГГц:

object := plot::Ode3d(f, [i/10 $ i=1..500], Y0,
           [Gxyz, Style = Splines, Color = RGB::Red],
           [Gyz, Style = Splines, Color = RGB::LightGrey],
           [Gxz, Style = Splines, Color = RGB::LightGrey],
           [Gxy, Style = Splines, Color = RGB::LightGrey]):

Мы задаем анимированную камеру, перемещающую сцену:

camera := plot::Camera([-1 + 100*cos(a), 6 + 100*sin(a), 120],
                       [-1, 6, 25], PI/6, a = 0..2*PI, 
                       Frames = 120):

Следующий вызов plot также берет о половине минуты на компьютере на 1 ГГц:

plot(object, camera, Axes = Boxed, TicksNumber = Low):

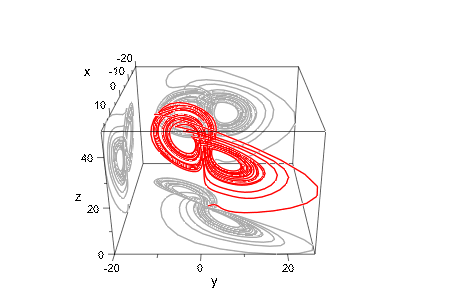
Затем, мы хотим полететь вдоль Аттрактора Лоренца. Мы не можем использовать plot::Ode3d, потому что нам нужен доступ к числовым данным аттрактора, чтобы создать подходящий анимированный объект камеры. Мы используем числовой решатель ОДУ numeric::odesolve2 и вычисляем список числовых точек выборки на Аттракторе Лоренца. Это берет о половине минуты на компьютере на 1 ГГц:

Y := numeric::odesolve2(f, 0, Y0, RememberLast):
timemesh :=  [i/50 $ i = 0..2000]:   
Y := [Y(t) $ t in timemesh]:

Подобно изображению выше, мы задаем поле вокруг аттрактора с проекциями кривой решения:

box := [-15, 20, -20, 26, 1, 50]:
Yyz := map(Y, pt -> [box[1], pt[2], pt[3]]):
Yxy := map(Y, pt -> [pt[1], pt[2], box[5]]):
Yxz := map(Y, pt -> [pt[1], box[3], pt[3]]):

Мы создаем анимированную камеру с помощью параметра анимации a, который соответствует индексу списка числовых точек выборки. Следующая процедура возвращает i-th координата (i = 1, 2, 3) a-th точка в списке точек выборки:

Point := proc(a, i)
begin
  if domtype(float(a)) <> DOM_FLOAT then
       procname(args());
  else Y[round(a)][i];
  end_if;
end_proc:

В a-th кадр анимации, камера расположена в a-th точка выборки Аттрактора Лоренца, указывающего на следующую точку выборки. Устанавливая TimeRange = 0..n/10, камера посещает приблизительно 10 точек в секунду:

n := nops(timemesh) - 1:
plot(plot::Scene3d(
   plot::Camera([Point(a, i)    $ i = 1..3], 
                [Point(a + 1, i) $ i = 1..3],
                 PI/4, a = 1..n, Frames = n, 
                 TimeRange = 0..n/10),
   plot::Polygon3d(Y, LineColor = RGB::Red, 
                   PointsVisible = TRUE),
   plot::Polygon3d(Yxy, LineColor = RGB::DimGrey),
   plot::Polygon3d(Yxz, LineColor = RGB::DimGrey),
   plot::Polygon3d(Yyz, LineColor = RGB::DimGrey),
   plot::Box(box[1]..box[2], box[3]..box[4], box[5]..box[6],
             LineColor = RGB::Black, Filled = TRUE,
             FillColor = RGB::Grey.[0.1]),
   BackgroundStyle = Flat)
):