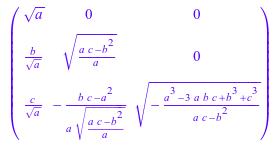Блокноты MuPAD® будут демонтированы в будущем релизе. Используйте live скрипты MATLAB® вместо этого.
Live скрипты MATLAB поддерживают большую часть функциональности MuPAD, хотя существуют некоторые различия. Для получения дополнительной информации смотрите, Преобразовывают Notebook MuPAD в Live скрипты MATLAB.
Факторизация Холесского выражает комплексную Эрмитовую (самопримыкающую) положительную определенную матрицу как продукт нижнего треугольного матричного L, и его Эрмитовы транспонируют L H: A = L LH. Эрмитовы транспонируют матрицы, сопряженное комплексное число транспонирования той матрицы. Для действительных и симметричных матриц транспонирование совпадает с Эрмитовым, транспонируют. Таким образом факторизацией Холесского действительной симметричной положительной определенной матрицы является A = L LT, где L T является транспонированием L.
Создайте 5×5 матрица Паскаля. Эта матрица симметрична и положительная определенный:
P := linalg::pascal(5)

Чтобы вычислить разложение Холесского матрицы, используйте функцию linalg::factorCholesky. Результатом является следующая нижняя треугольная матрица:
L := linalg::factorCholesky(P)

Продукт треугольной матрицы L и транспонировать дает исходный матричный P:
testeq(P = L*linalg::transpose(L))
![]()
MuPAD® возвращает нижнюю треугольную матрицу в результате факторизации Холесского. MATLAB® возвращает верхнюю треугольную матрицу, которая является транспонированием результата, возвращенного MuPAD.
Когда MuPAD не может определить, является ли матрица Эрмитовой, linalg::factorCholesky выдает ошибку:
A := matrix([[a, b, c], [b, c, a], [c, a, b]]): linalg::factorCholesky(A)
Error: Hermitian matrix expected. [linalg::factorCholesky]
Если вы знаете, что матрица является Эрмитовой, можно подавить эту ошибку. Опция NoCheck подавляет ошибку и позволяет linalg::factorCholesky функционировать, продолжают вычисление:
linalg::factorCholesky(A, NoCheck)
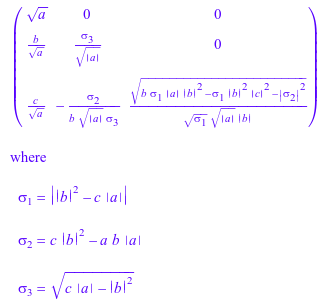
Если вы знаете, что матрица действительна и симметрична, используйте опцию Real, чтобы избежать сопряженных комплексных чисел (подразумеваемый |a | = a *ā) в результате:
linalg::factorCholesky(A, NoCheck, Real)