linalg:: factorCholeskyРазложение Холесского матрицы
Блокноты MuPAD® будут демонтированы в будущем релизе. Используйте live скрипты MATLAB® вместо этого.
Live скрипты MATLAB поддерживают большую часть функциональности MuPAD, хотя существуют некоторые различия. Для получения дополнительной информации смотрите, Преобразовывают Notebook MuPAD в Live скрипты MATLAB.
linalg::factorCholesky(A, <NoCheck>, <Real>)
linalg::factorCholesky(A) вычисляет факторизацию Холесского Эрмитового положительного определенного матричного A и возвращает нижний треугольный матричный L, такой что L LH = A. Здесь, L H является Эрмитовым сопряженным из L (сопряженное комплексное число транспонирования).
Звонок компонента A должен быть полем (область категории Cat::Field).
Если A не является Эрмитовой положительной определенной матрицей, то linalg::factorCholesky выдает ошибку. Если вы используете NoCheck, linalg::factorCholesky не проверяет, является ли матрица Эрмитовой положительный определенный. Смотрите Пример 2.
Если вы используете Real, то linalg::factorCholesky принимает, что A действителен и симметричен и, поэтому, не применяет сопряженное комплексное число в ходе алгоритма.
linalg::factorCholesky возвращает FAIL, если этому не удается вычислить матричный L по звонку компонента A. (Алгоритм требует вычисления квадратных корней из некоторых элементов в L).
Свойства идентификаторов учтены.
Задайте матричный S можно следующим образом:
S := Dom::Matrix(Dom::Rational)( [[4, -2, 4, 2], [-2, 10, -2, -7], [4, -2, 8, 4], [2, -7, 4, 7]] )

Вычислите факторизацию Холесского S:
L := linalg::factorCholesky(S)

Проверьте результат:
is(L * htranspose(L) = S)
![]()
Задайте матричный H можно следующим образом:
H := matrix([[a, b], [b, a]])
![]()
linalg::factorCholesky не может вычислить факторизацию Холесского, потому что не может оказаться, что H является Эрмитова матрица:
linalg::factorCholesky(H)
Error: Hermitian matrix expected. [linalg::factorCholesky]
Если вы принимаете, что a и b действительны, то матричный H является Эрмитовым. Однако, linalg::factorCholesky не может вычислить факторизацию Холесского:
linalg::factorCholesky(H) assuming a in R_ and b in R_
Error: Unable to check whether the matrix component is positive. [linalg::factorCholesky]
Используйте опцию NoCheck, чтобы пропустить проверку, является ли эта матрица Эрмитовой положительный определенный. Теперь, linalg::factorCholesky вычисляет факторизацию:
L := linalg::factorCholesky(H, NoCheck)
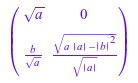
Этот результат не обычно допустим:
L*htranspose(L) = H
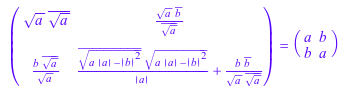
Это допустимо для 0 < a < b:
simplify(L*htranspose(L) = H) assuming 0 < b < a
![]()
Вычислите факторизацию Холесского матричного H с помощью NoCheck, чтобы пропустить проверку, является ли это Эрмитовым положительный определенный. По умолчанию linalg::factorCholesky вычисляет Эрмитовую факторизацию A = L LH. Таким образом результат содержит сопряженные комплексные числа (подразумеваемый |a | = a *ā).
H := matrix([[a, b], [b, a]]): L := linalg::factorCholesky(H, NoCheck)
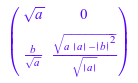
Чтобы избежать сопряженных комплексных чисел в результате, используйте Real:
L := linalg::factorCholesky(H, NoCheck, Real)
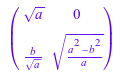
При использовании этой опции linalg::factorCholesky вычисляет симметричную факторизацию A = L Lt вместо Эрмитовой факторизации A = L LH:
simplify(L*transpose(L) = H)
![]()
|
Квадратная матрица области категории |
|
Пропустите проверку, является ли |
|
Вычислите факторизацию Холесского, принимающую, что матричный A симметричен, и все его символьные параметры действительны. В этом случае транспонирование матрицы является своим Эрмитовым, транспонируют. Используйте эту опцию, если A содержит символьные параметры, и вы хотите избежать сопряженных комплексных чисел. При использовании этой опции идентичность L LT = A, как гарантируют, будет содержать. |
Матрица того же доменного типа как A или значение FAIL.
Факторизация Холесского Эрмитового положительного определенного n ×n матричный A является разложением A в продукте L LH = A, такой, что L является нижней треугольной матрицей с положительными записями на основной диагонали. L называется “Фактором Холесского” A.
Если L = (l i, j), где 1 ≤ i ≤ n, 1 ≤ j ≤ n, является Фактор Холесского A, то![]() .
.