Блокноты MuPAD® будут демонтированы в будущем релизе. Используйте live скрипты MATLAB® вместо этого.
Live скрипты MATLAB поддерживают большую часть функциональности MuPAD, хотя существуют некоторые различия. Для получения дополнительной информации смотрите, Преобразовывают Notebook MuPAD в Live скрипты MATLAB.
Меры формы указывают на симметрию и плоскость распределения выборки данных. MuPAD® обеспечивает следующие функции для вычисления мер формы:
Функция stats::moment, которая вычисляет k-th момент
из выборки данных x 1, x 2, ..., x n, сосредоточенный вокруг X.
Функция stats::obliquity, которая вычисляет косое направление (скошенность)
,
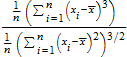где
является средним арифметическим (среднее значение) выборки данных x 1, x 2, ..., x n.
Функция stats::kurtosis, которая вычисляет эксцесс (избыток)
,
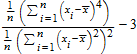где
является средним арифметическим (среднее значение) выборки данных x 1, x 2, ..., x n.
Функция stats::moment позволяет вам вычислить k th момент выборки данных, сосредоточенной вокруг произвольного значения X. Одной из популярных мер в описательной статистике является центральный момент. k th центральный момент выборки данных является k th момент, сосредоточенный вокруг среднего арифметического (среднее значение) той выборки данных. Следующие операторы допустимы для любой выборки данных:
Нулевой центральный момент всегда равняется 1.
Первый центральный момент всегда 0.
Второй центральный момент равен отклонению, вычисленному при помощи делителя n, а не n - 1 (доступный с помощью опции Population stats::variance).
Например, создайте списки L и S можно следующим образом:
L := [1, 1, 1, 1, 1, 1, 1, 1, 100.0]: S := [100, 100, 100, 100, 100, 100, 100, 100, 1.0]:
Вычислите среднее арифметическое каждого списка при помощи функции stats::mean:
meanL := stats::mean(L); meanS := stats::mean(S)
Вычислите первые четыре центральных момента списка L:
stats::moment(0, meanL, L), stats::moment(1, meanL, L), stats::moment(2, meanL, L), stats::moment(3, meanL, L)
Нуль и сначала центральные моменты является тем же самым для любой выборки данных. Вторым центральным моментом является отклонение, вычисленное с делителем n:
stats::variance(L, Population)
Теперь, вычислите первые четыре центральных момента списка S:
stats::moment(0, meanS, S), stats::moment(1, meanS, S), stats::moment(2, meanS, S), stats::moment(3, meanS, S)
Снова, нулевой центральный момент равняется 1, первый центральный момент 0, и вторым центральным моментом является отклонение, вычисленное с делителем n:
stats::variance(S, Population)
Косое направление (скошенность) является мерой симметрии распределения. Если распределение близко к симметричному вокруг его среднего значения, значение косого направления близко к нулю. Положительные значения косого направления указывают, что функция распределения имеет более длинный хвост справа от среднего значения. Отрицательные величины указывают, что функция распределения имеет более длинный хвост слева от среднего значения. Например, вычислите косое направление списков L и S:
stats::obliquity(L); stats::obliquity(S)
Эксцесс измеряет плоскость распределения. Для нормально распределенных данных эксцесс является нулем. Отрицательный эксцесс указывает, что функция распределения имеет более плоскую верхнюю часть, чем нормальное распределение. Положительный эксцесс указывает, что пик функции распределения более резок, чем это для нормального распределения:
stats::kurtosis(-2, -1, -0.5, 0, 0.5, 1, 2), stats::kurtosis(-1, 0.5, 0, 0, 0, 0, 0.5, 1)
