Блокноты MuPAD® будут демонтированы в будущем релизе. Используйте live скрипты MATLAB® вместо этого.
Live скрипты MATLAB поддерживают большую часть функциональности MuPAD, хотя существуют некоторые различия. Для получения дополнительной информации смотрите, Преобразовывают Notebook MuPAD в Live скрипты MATLAB.
QR-факторизация выражает m ×n матричный A можно следующим образом: A = Q*R. Здесь Q является m ×m унитарная матрица, и R является m ×n верхняя треугольная матрица. Если компоненты A являются вещественными числами, Q является ортогональной матрицей. Чтобы вычислить разложение QR матрицы, используйте функцию linalg::factorQR. Например, вычислите разложение QR 3×3 матрица Паскаля:
P := linalg::pascal(3): [Q, R] := linalg::factorQR(P)
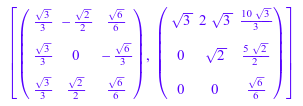
Продукт Q и R дает оригиналу 3×3 матрицу Паскаля:
testeq(P = Q*R)
![]()
Кроме того, можно выполнить QR-факторизацию для матриц, которые содержат комплексные числа. В этом случае матричный Q унитарен:
B := matrix([[I, -1], [1, I]]): [Q, R] := linalg::factorQR(B)
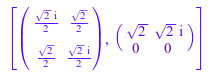
Снова, продукт Q и R дает исходный матричный B:
testeq(B = Q*R)
![]()