Документация

Многомерная регрессия

Функция stats::reg также выполняет линейные и нелинейные регрессии с двумя или больше независимыми переменными. Следующий пример демонстрирует, как выполнить регрессию и соответствовать данным к функции двух переменных. Предположим, у вас есть три списка данных, которые содержат, координирует x, y и z дискретных точек:

sampleX := [
   -0.9612553839, -0.329576986, 0.7544749248, 0.7339191669,
   -0.294101483, -0.9809519422, -0.6251624775, -0.1885706545,
    0.4729466504, 0.4402179092, -0.1883574567, -0.6260246367,
   -0.0274947885, -0.01843922645, -0.02687538212, -0.03682895886,
   -0.009212115975, -0.04956242636]:
sampleY := [
   -0.02185415496, -0.9146217269, -0.5792023459, 0.5440822742,
    0.8848317212, -0.03925037966, -0.02360776024, -0.5657632266,
   -0.3461422332, 0.3429495709, 0.5113552882, -0.02089004809,
   -0.03700165982, -0.0226531849, -0.004897297126, -0.03063832565,
   -0.03469956571, -0.01391540741]:
sampleZ := [
    0.2755344332, 0.272077192, 0.2682296712, 0.2915713541,
    0.2737466882, 0.3060314064, 0.7624231851, 0.8013891042,
    0.7755723041, 0.7631156115, 0.7816602999, 0.7807856826,
    0.9679031724, 0.9661527172, 0.9632260164, 0.986479402,
    0.9554368723, 0.9768285979]:

Предположим, вы хотите найти поверхность, которая соответствует этим точкам. Запустите с отображения на графике данных. Функция plot::PointList3d, которая строит конечное число дискретных точек, требует, чтобы координаты каждой точки группировались. Следующие команды создают отдельные списки для координат каждой точки: [x _i, y _i, z _i] и помещенный эти списки в один вложенный список:

points := [[sampleX[i], sampleY[i], sampleZ[i]]
                        $ i = 1..nops(sampleX)]:

Теперь, используйте функцию plot::PointList3d, чтобы визуализировать данные:

plot1 := plot::PointList3d(points, PointSize = 2.5):
plot(plot1)

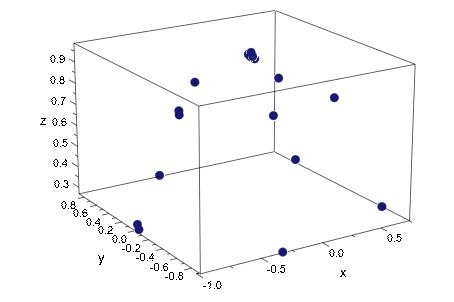
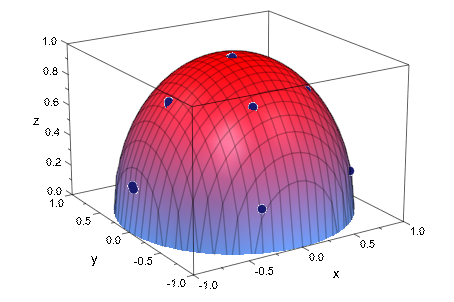
Вращение графика может помочь вам предположить, какая поверхность может возможно соответствовать данным. Этот график показывает, что данные могут принадлежать верхней половине сферы. Таким образом попытайтесь соответствовать данным к сфере с неизвестным радиусом r. Функция stats::reg ищет значение оптимальной подгонки для параметра r:

fit := stats::reg(sampleX, sampleY, sampleZ,
     sqrt(r^2 - x1^2 - y1^2), [x1, y1], [r])

Функция stats::reg также принимает вложенный список points:

fit := stats::reg(points, sqrt(r^2 - x1^2 - y1^2),
                                    [x1, y1], [r])

Функция stats::reg возвращает параметры модели и квадратичной ошибки в форме вложенного списка. Чтобы получить доступ к параметрам отдельно, используйте следующие команды:

R := op(fit)[1][1];
chi2 := op(fit)[2]

Теперь, отобразите на графике данные и сферу, что вы раньше соответствовали данным по тому же графику. Вращайте график, чтобы видеть, как сфера соответствует данным:

plot2 := plot::Function3d(sqrt(R^2 - x^2 - y^2),
                          x = -1..1, y = -1..1):
plot(plot1, plot2)