статистика::Регрессия (общий линейный и подгонка нелинейного метода наименьших квадратов)
Блокноты MuPAD® будут демонтированы в будущем релизе. Используйте live скрипты MATLAB® вместо этого.
Live скрипты MATLAB поддерживают большую часть функциональности MuPAD, хотя существуют некоторые различия. Для получения дополнительной информации смотрите, Преобразовывают Notebook MuPAD в Live скрипты MATLAB.
stats::reg([x1, 1, …,xk, 1], …,[x1, m, …,xk, m],[y1, …,yk], <[w1, …,wk]>,f,[x1, xm],[p1, …,pn], <StartingValues = [p1(0), …,pn(0)]>, <CovarianceMatrix>) stats::reg([[x1, 1, …,x1, m, y1, <w1>], …,[xk, 1, …,xk, m, yk, <wk>]],f,[x1, …,xm],[p1, …,pm], <StartingValues = [p1(0), …,pn(0)]>, <CovarianceMatrix>) stats::reg(s,c1, …,cm,cy, <cw>,f,[x1, …,xm],[p1, …,pn], <StartingValues = [p1(0), …,pn(0)]>, <CovarianceMatrix>) stats::reg(s,[c1, cm],cy, <cw>,f,[x1, …,xm],[p1, …,pn], <StartingValues = [p1(0), …,pn(0)]>, <CovarianceMatrix>)
Считайте “образцовый функциональный” f с параметрами n p 1, …, p n, связывающий зависимую переменную y и независимые переменные m x 1, …, x m: y = f (x 1, …, x m, p 1, …, p n). Учитывая k различные измерения x 1 j, …, x kj для независимых переменных x j и соответствующие измерения y 1, …, y k для зависимой переменной y, каждый соответствует параметрам p 1, …, p n путем минимизации “взвешенного квадратичного отклонения”, (“в квадрате хи”)
.
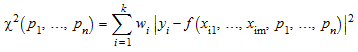stats::reg(..data.., f, [x.1, ... , x.m], [p.1, ... , p.n], [w.1, ..., w.n]) вычисляет числовые приближения подходящих параметров p 1, …, p n.
Все данные должны быть конвертируемыми к действительному или объединить значения с плавающей точкой через float.
Количество измерений k не должно быть меньше, чем номер n параметров p i.
Образцовый функциональный f может быть нелинейным в независимых переменных x i и подходящие параметры p i. Например, образцовая функция, такая как p1 + p2*x1^2 + exp(p3 + p4*x2) с независимыми переменными x1, x2 и подходящие параметры p1, p2, p3, p4 принята.
Обратите внимание на то, что подбор кривой образцовых функций с нелинейной зависимостью от параметров p, i является намного более дорогостоящим, чем линейная регрессия, где i p входят линейно. Функциональная зависимость образцовой функции на переменных x i не имеет уместности.
Существуют редкие случаи, где реализованный алгоритм сходится к локальному минимуму, а не к глобальному минимуму. В частности, эта проблема может возникнуть, когда модель включает периодические функции. Рекомендуется обеспечить подходящие начальные значения для подходящих параметров в этом случае. Cf. Пример 4.
Внешние статистические данные, сохраненные в ASCII-файле, могут быть импортированы в сеанс MuPAD® через import::readdata. В частности, смотрите Пример 1 из соответствующей страницы справки.
Функция чувствительна к переменной окружения DIGITS, который определяет числовую рабочую точность.
Мы соответствуем линейной функции y = p 1 + p 2 x1 к четырем парам данных (x i1, y i) данный двумя списками:
stats::reg([0, 1, 2, 3], [1, 3, 5, 7],
p1 + p2*x1, [x1], [p1, p2])
Значения параметров p 1 = 1.0, p 2 = 2.0 обеспечивает совершенную подгонку: до числового округления исчезает квадратичное отклонение.
Мы соответствуем показательной функции y = a eb x к пяти парам данных (x i, y i). Веса используются, чтобы уменьшить влияние “исключительной пары” (x, y) = (5.0, 6.5×106) на подгонке:
stats::reg([[1.1, 54, 1], [1.2, 73, 1], [1.3, 98, 1],
[1.4, 133, 1], [5.0, 6.5*10^6, 10^(-4)]],
a*exp(b*x), [x], [a, b])
Мы создаем выборку с четырьмя столбцами. Первый столбец является счетчиком, маркирующим измерения. Этот столбец не имеет дальнейшей уместности здесь. Второй и третий столбец обеспечивает результаты измерений двух переменных x 1 и x 2, соответственно. Последний столбец обеспечивает соответствующие измерения зависимой переменной.
s := stats::sample([[1, 0, 0, 1.1], [2, 0, 1, 5.4],
[3, 1, 1, 8.5], [4, 1, 2, 18.5],
[5, 2, 1, 15.0], [6, 2, 2, 24.8]])1 0 0 1.1 2 0 1 5.4 3 1 1 8.5 4 1 2 18.5 5 2 1 15.0 6 2 2 24.8
Во-первых, мы пытаемся смоделировать данные, обеспеченные столбцами 2, 3, 4 функцией, которая линейна в переменных x 1, x 2. Мы задаем столбцы данных списком индексов столбца:
stats::reg(s, [2, 3, 4], p1 + p2*x1 + p3*x2,
[x1, x2], [p1, p2, p3])
Квадратичное отклонение является довольно большим, указывая, что линейная функция является несоответствующей, чтобы соответствовать данным. Затем, мы расширяем модель и рассматриваем функцию аппроксимации полиномом степени 2. Это - все еще проблема линейной регрессии, потому что подходящие параметры вводят образцовую функцию линейно. Мы задаем столбцы данных последовательностью индексов столбца:
stats::reg(s, 2, 3, 4,
p1 + p2*x1 + p3*x2 + p4*x1^2 + p5*x2^2,
[x1, x2], [p1, p2, p3, p4, p5])
Наконец, мы включаем дальнейший термин p6*x1*x2 в модель, получая совершенную подгонку:
stats::reg(s, 2, 3, 4,
p1 + p2*x1 + p3*x2 + p4*x1^2 + p5*x2^2 + p6*x1*x2,
[x1, x2], [p1, p2, p3, p4, p5, p6])
delete s:
Мы создаем выборку двух столбцов:
s := stats::sample([[1, -1.44], [2, -0.82],
[3, 0.97], [4, 1.37]])1 -1.44 2 -0.82 3 0.97 4 1.37
Данные должны быть смоделированы функцией формы y = p 1 sin (p 2 x), где первый столбец содержит измерения x, и второй столбец содержит соответствующие данные для y. Обратите внимание на то, что в этом примере нет никакой потребности задать индексы столбца, потому что выборка содержит только два столбца:
stats::reg(s, a*sin(b*x), [x], [a, b])
Подбор кривой периодической функции может быть проблематичным. Мы обеспечиваем начальные значения для подходящих параметров и получаем очень отличающийся набор параметров, аппроксимирующих данные с тем же качеством:
stats::reg(s, a*sin(b*x), [x], [a, b], StartingValues = [2, 5])
delete s:
Уровень сахара в крови y (в mmol/L) диабетика измеряется в течение 10 дней с 5 измерениями в день в x1 = 7 (час утра), x1 = 12 (полдень), x1 = 15 (день), x1 = 19 (перед ужином), и x1 = 23 (время ложиться спать). Это измерения:
Y:= //hour: 7 12 15 19 23
[ [ 7.2, 5.5, 6.8, 5.4, 6.0], // day 1
[ 6.3, 5.0, 5.5, 5.8, 4.9], // day 2
[ 6.5, 6.3, 4.8, 4.5, 5.0], // day 3
[ 4.3, 5.2, 4.3, 4.7, 4.0], // day 4
[ 7.1, 7.2, 6.7, 7.2, 5.5], // day 5
[ 5.8, 5.5, 4.9, 5.0, 6.2], // day 6
[ 6.2, 4.8, 5.0, 5.2, 5.3], // day 7
[ 4.8, 5.8, 5.7, 6.2, 5.0], // day 8
[ 5.2, 3.8, 4.8, 5.8, 4.7], // day 9
[ 5.8, 4.7, 5.0, 6.5, 6.3] // day 10
]:У нас есть в общей сложности 50 измерений. Каждым измерением является тройной [x1, x2, y], где x1 является часом дня, x2 является дневным номером, и y является уровнем сахара в крови:
data:= [([ 7, x2, Y[x2][1]],
[12, x2, Y[x2][2]],
[15, x2, Y[x2][3]],
[19, x2, Y[x2][4]],
[23, x2, Y[x2][5]]
) $ x2 = 1 .. 10]:Мы моделируем сахар в крови y как функция часа дня x1 и дневной номер x2 (пытающийся обнаружить общую тенденцию). Мы принимаем периодическую зависимость от x1 с периодом 24 часов:
y := y0 + a*x2 + b*sin(2*PI/24*x1 + c):
Метод наименьших квадратов определенных данных приводит к следующим параметрам y0, a, b, c:
[y0abc, residue]:= stats::reg(data, y, [x1, x2], [y0, a, b, c]): [y0, a, b, c]:= y0abc
Средним уровнем сахара в крови является y0 =
с улучшением a =
в день. Амплитудой ежедневного изменения y является b =
. Мы визуализируем измерения Y plot::Matrixplot. Метод наименьших квадратов нашего образцового функционального y добавляется как функциональный график:
plot(plot::Matrixplot(Y, x1 = 0..24, x2 = 1..10),
plot::Function3d(y, x1 = 0..24, x2 = 1..10,
Color = RGB::Green))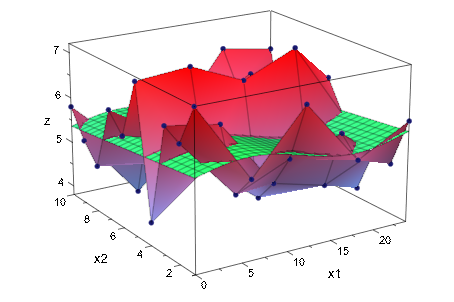
delete Y, data, y, y0abc, y0, a, b, c, residue:
Мы рассматриваем затухающий радиоактивный источник, действие которого N (“количества”) измеряется с промежутками в 1 секунду. Физическая модель для затухания
, где N (t) является уровнем количества во время t, N 0 является базовой ставкой во время, t = 0 и τ является временем жизни радиоактивного источника. Вместо того, чтобы брать данные из фактического физического эксперимента, мы создаем искусственные данные с базовой ставкой N 0 = 100 и время жизни τ = 300:
T := [i $ i= 0 .. 100]: N := [100*exp(-t/300) $ t in T]:
Конструкцией мы получаем совершенную подгонку при оценке параматерей N 0 и τ модели:
stats::reg(T, N, N0*exp(-t/tau), [t], [N0, tau]);
Мы тревожим данные:
N := [stats::poissonRandom(n)() $ n in N]:
Начиная с данных n i в N является Poissonian, их стандартное отклонение является квадратным корнем из их среднего значения
:. таким образом подходящими весами для оценки методом наименьших квадратов параметров дают
:
W := [1/n $ n in N]:
С этими весами методом наименьших квадратов параметров модели вычисляются N 0 и τ. Опция CovarianceMatrix используется, чтобы получить информацию о доверительных интервалах для параметров:
[p, chisquared, C] :=
stats::reg(T, N, W, N0*exp(-t/tau), [t], [N0, tau],
CovarianceMatrix)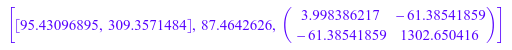
Квадратные корни из диагональных элементов ковариационной матрицы обеспечивают статистические стандартные отклонения подходящих параметров:
sqrt(float(C[1,1])), sqrt(float(C[2,2]))
Таким образом оценка для базовой ставки, которая N 0
, оценка для пожизненного τ
. Корреляционная матрица подходящих параметров получена из ковариационной матрицы через stats::correlationMatrix:
stats::correlationMatrix(C)
delete T, N, W, p, chisquared, C:
|
Числовые выборочные данные для независимых переменных. Запись x i, j представляет i-th измерение независимой переменной x j. |
|
Числовые выборочные данные для зависимой переменной. Запись y i представляет i-th измерение зависимой переменной. |
|
Весовые коэффициенты: положительные действительные численные значения. Запись w i используется в качестве веса для данных x i, 1, …, x i, m, y i i-th измерение. Если никакие веса не обеспечиваются, то w i = 1 используется. |
|
Образцовая функция: арифметическое выражение, представляющее функцию независимых переменных x 1, …, x m и подходящие параметры p 1, …, p n. Выражение не должно содержать символьные объекты кроме x 1, …, x m, p 1, …, p n. |
|
Независимые переменные: идентификаторы или индексированные идентификаторы. |
|
Подходящие параметры: идентификаторы или индексированные идентификаторы. |
|
Пользователь может помочь внутреннему числовому поиску путем обеспечения числовым начальным значениям p i (0) для подходящих параметров p i. Они должны быть обоснованно близко к оптимальным подходящим значениям. i p начальных значений (0) = 1.0 используется, если никакие начальные значения не обеспечиваются пользователем. |
|
Выборка доменного типа |
|
Положительное целое число, представляющее индекс столбца демонстрационного |
|
Положительное целое число, представляющее индекс столбца демонстрационного |
|
Опция, заданная как Положительные целые числа, представляющие индексы столбца демонстрационного Если образцовая функция зависит линейно от подходящих параметров p j (“линейная регрессия”), то оптимизированные параметры являются решением линейной системы уравнений. В этом случае нет никакой потребности обеспечить начальные значения для числового поиска. На самом деле начальные значения, обеспеченные пользователем, проигнорированы. Если образцовая функция зависит нелинейно от подходящих параметров p j (“нелинейная регрессия”), то оптимизированные подгоняемые параметры являются решением нелинейной задачи оптимизации. Нет никакой гарантии, что внутренний поиск числового решения успешно выполнится. Рекомендуется помочь внутреннему решателю путем обеспечения довольно хороших оценок для оптимальных подходящих параметров. |
|
Изменяет возвращаемое значение от [[p 1, …, p n], χ 2] к [[p 1, …, p n], χ 2, C], где C является ковариационной матрицей средств оценки p i, данный C i, i = σ (p i) 2 и C i, j = cov (p i, p j) для i ≠ j. При использовании этой опции, информацией о доверительных интервалах для оценочных функций методом наименьших квадратов p i обеспечиваются. В частности, возвращаемое значение включает ковариационную матрицу C типа
Где
Ковариационная матрица оценочных функций методом наименьших квадратов только имеет статистическое значение, если стохастические отклонения σ (y i) 2 из измерений y i известны. Эти отклонения должны быть включены в вычисление путем выбора весов Функциональный |
Без опции CovarianceMatrix, список [[p 1, …, p n], возвращен χ 2]. Это содержит оптимизированные подходящие параметры p i, минимизирующий квадратичное отклонение. Минимизированное значение этого отклонения дано χ 2, это указывает на качество подгонки.
С опцией CovarianceMatrix, список [[p 1, …, p n], χ 2, возвращен C]. n ×n матричный C является ковариационной матрицей подходящих параметров.
Все возвращенные данные являются значениями с плавающей точкой. FAIL возвращен, если припадок наименьшего квадрата данных не возможен с данной образцовой функцией или если внутренний числовой поиск перестал работать.
П.Р. Бевингтон и Д.К. Робинсон, “Снижение объема данных и анализ ошибок для физики”, McGraw-Hill, Нью-Йорк, 1992.
stats::reg использует алгоритм расширения градиента Marquardt-Levenberg. Ища минимум
, алгоритм просто не следует за отрицательным градиентом, но диагональные термины матрицы искривления увеличены фактором, который оптимизирован на каждом шаге поиска.
,
.