От анализа Фурье до анализа вейвлета

Скалярные произведения

И Фурье и вейвлет преобразовывают подобие меры между сигналом и функцией анализа. Оба преобразовывает, используют математический инструмент, названный скалярным произведением как эта мера подобия. Два преобразовывают, отличаются по их выбору анализа функции. Это заканчивается различным способом, которым преобразовывают два, представляют сигнал и какая информация может быть извлечена.

Как простой пример скалярного произведения как мера подобия, рассмотрите скалярное произведение векторов в плоскости. Следующий пример MATLAB^® вычисляет скалярное произведение трех единичных векторов, ${u, v, w}$ , в плоскости:

$\begin{array}{l} {(\begin{matrix} \sqrt{3} / 2 \\ 1 / 2 \end{matrix}), (\begin{matrix} 1 / \sqrt{2} \\ 1 / \sqrt{2} \end{matrix}), (\begin{matrix} 01 \end{matrix})} \end{array}$

u = [sqrt(3)/2 1/2];
v = [1/sqrt(2) 1/sqrt(2)];
w = [0 1];
% Three unit vectors in the plane
quiver([0 0 0],[0 0 0],[u(1) v(1) w(1)],[u(2) v(2) w(2)]);
axis([-1 1 0 1]);
text(-0.020,0.9371,'w');
text(0.6382,0.6623,'v');
text(0.7995,0.4751,'u');
% Compute inner products and print results
fprintf('The inner product of u and v is %1.2f\n', dot(u,v))
fprintf('The inner product of v and w is %1.2f\n', dot(w,v))
fprintf('The inner product of u and w is %1.2f\n', dot(u,w))

Смотря на фигуру, ясно, что u и v являются самыми подобными в их ориентации, в то время как u и w наиболее отличаются.

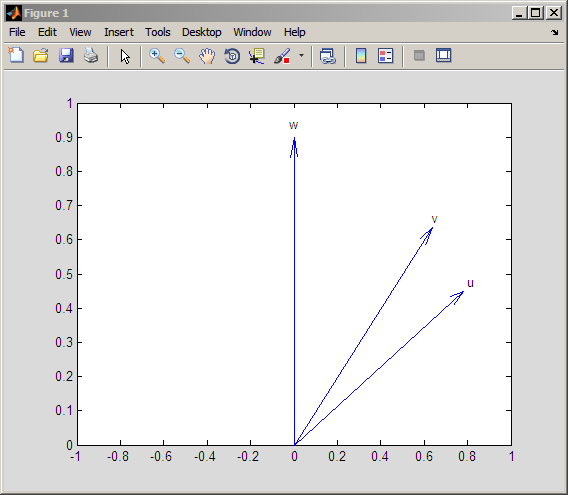
Скалярные произведения получают этот геометрический факт. Математически, скалярное произведение двух векторов, u и v равно продукту их норм и косинусу угла, θ, между ними:

$\begin{array}{l} < u, v > = | | u | | | | v | | потому что (θ) \end{array}$

Для особого случая, когда и u и v имеют модульную норму или модульную энергию, скалярное произведение равно тому, потому что (θ), и поэтому находится между [-1,1]. В этом случае можно интерпретировать скалярное произведение непосредственно как коэффициент корреляции. Если или u или v не имеют модульной нормы, скалярное произведение может превысить 1 в абсолютном значении. Однако скалярное произведение все еще зависит от косинуса угла между этими двумя векторами, делающими его поддающийся толкованию как своего рода корреляция. Обратите внимание на то, что абсолютное значение скалярного произведения является самым большим, когда угол между ними или 0 или $π$ радианы (0 или 180 градусов). Это происходит, когда один вектор является скалярным кратным с действительным знаком другой.

В то время как скалярные произведения на более многомерных пробелах как те, с которыми сталкиваются в Фурье и вейвлете преобразовывают, не показывают ту же простоту геометрической интерпретации как предыдущий пример, они измеряют подобие таким же образом. Значительная часть утилиты этих преобразований - то, что они по существу обобщают корреляцию между сигналом и некоторыми основными функциями с определенными физическими свойствами, как частота, шкала или положение. Путем суммирования сигнала в этих составных частях мы можем лучше понять механизмы, которые произвели сигнал.

Преобразование Фурье

Анализ Фурье используется в качестве отправной точки, чтобы ввести вейвлет, преобразовывает, и в качестве сравнительного теста, чтобы продемонстрировать случаи, где анализ вейвлета обеспечивает более полезную характеристику сигналов, чем анализ Фурье.

Математически, процесс анализа Фурье представлен преобразованием Фурье:

$F (ω) = \int_{- \infty}^{\infty} f (t) e^{- j ω t} d t .$

который является интегралом (сумма) за все время сигнала f (t), умноженного на комплексный экспоненциал. Вспомните, что комплексный экспоненциал может быть разломан на действительные и мнимые синусоидальные компоненты. Обратите внимание на то, что преобразование Фурье сопоставляет функцию одной переменной в другую функцию одной переменной.

Интеграл, задающий преобразование Фурье, является скалярным произведением. Смотрите Скалярные произведения для примера как мера по скалярным произведениям подобия между двумя сигналами. Для каждого значения ω интеграл (или сумма) по всем значениям времени производит скаляр, F (ω), который подводит итог, насколько подобный два сигнала. Эти скаляры с комплексным знаком являются коэффициентами Фурье. Концептуально, умножая каждый коэффициент Фурье, F (ω), комплексным экспоненциалом (синусоида) частоты ω приводит к составляющим синусоидальным компонентам исходного сигнала. Графически, процесс похож

Поскольку $e^{j ω t}$ с комплексным знаком, F (ω), в целом, с комплексным знаком. Если сигнал содержит значительные колебания на угловой частоте $ω_{0}$ , абсолютное значение $F (ω_{0})$ будет большим. Путем исследования графика $| F (ω) |$ как функция угловой частоты, возможно определить то, что частоты вносят больше всего в изменчивость f (t).

Чтобы проиллюстрировать, как преобразование Фурье получает подобие между сигналом и синусоидами различных частот, следующий код MATLAB анализирует сигнал, состоящий из двух синусоид 4 и 8 герц (Гц), поврежденных аддитивным шумом с помощью дискретного преобразования Фурье.

rng(0,'twister');
Fs = 128;
t = linspace(0,1,128);
x = 2*cos(2*pi*4*t)+1.5*sin(2*pi*8*t)+randn(size(t));
xDFT = fft(x);
Freq = 0:64;
subplot(211);
plot(t,x); xlabel('Seconds'); ylabel('Amplitude');
subplot(212);
plot(Freq,abs(xDFT(1:length(xDFT)/2+1)))
set(gca,'xtick',[4:4:64]);
xlabel('Hz'); ylabel('Magnitude');

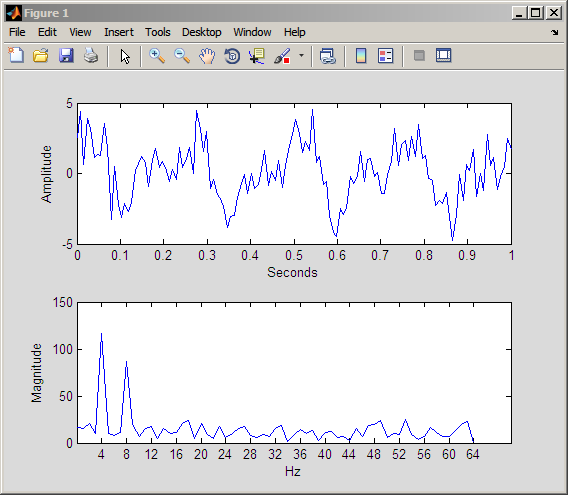
Просматриваемый как сигнал времени, трудно определить, какие значительные колебания присутствуют в данных. Однако смотря на абсолютное значение коэффициентов преобразования Фурье как функция частоты, доминирующие колебания на уровне 4 и 8 Гц легко обнаружить.

Кратковременное преобразование Фурье

Преобразование Фурье обобщает подобие между сигналом и синусоидой с одним комплексным числом. Значение комплексного числа получает степень, до которой колебания на особой частоте способствуют энергии сигнала, в то время как аргумент комплексного числа получает информацию о фазе. Обратите внимание на то, что у коэффициентов Фурье нет времени зависимость. Коэффициенты Фурье получены путем интеграции, или подведение итогов, за все время, таким образом, ясно, что эта информация потеряна. Рассмотрите следующие два сигнала:

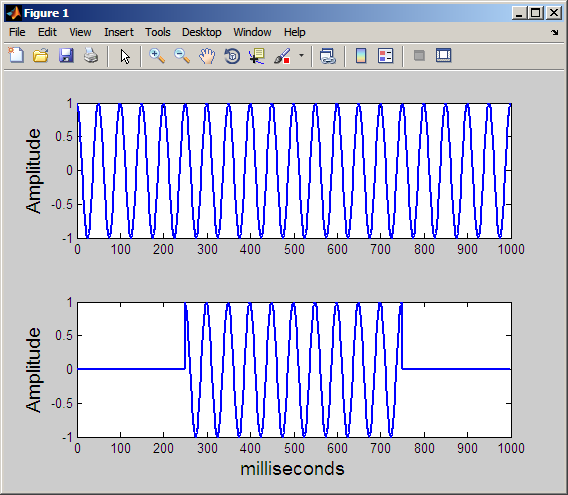
Оба сигнала состоят из одной синусоиды с частотой 20 Гц. Однако в главном сигнале, синусоида длится целые 1 000 миллисекунд. В нижнем графике синусоида запускается в 250 и заканчивается в 750 миллисекундах. Преобразование Фурье обнаруживает, что два сигнала имеют то же содержимое частоты, но не имеет никакого способа получить это, длительность колебания на 20 Гц отличается между двумя сигналами. Далее, преобразование Фурье не имеет никакого механизма для маркировки начала и конца неустойчивой синусоиды.

Чтобы исправить этот дефицит, Деннис Габор (1946) адаптировал преобразование Фурье, чтобы анализировать только небольшой раздел сигнала за один раз - метод вызвал работу с окнами сигнал. Адаптация Габора называется кратковременным преобразованием Фурье (STFT). Метод работает путем выбора функции времени или окна, которое является чрезвычайно ненулевым только на конечном интервале. Как один пример рассматривают следующую функцию окна Gaussian:

$w (t) = \sqrt{\frac{α}{π}} e^{- α t^{2}}$

Гауссова функция сосредоточена вокруг t=0 через определенный интервал, который зависит от значения α. Сдвиг Гауссовой функции τ приводит к:

$w (t - τ) = \sqrt{\frac{α}{π}} e^{- α {(t - τ)}^{2}},$

который сосредотачивает окно Gaussian вокруг τ. Умножение сигнала $w (t - τ)$ выбирает фрагмент сигнала, сосредоточенного в τ. При взятии преобразования Фурье этих оконных сегментов для различных значений τ, производит STFT. Математически, это:

$F (ω, τ) = \int f (t) w (t - τ) e^{- j ω t} d t$

STFT сопоставляет функцию одной переменной в функцию двух переменных, ω и τ. Это 2D представление 1D сигнала означает, что существует сокращение в STFT. Следующая фигура демонстрирует, как STFT сопоставляет сигнал в представление частоты времени.

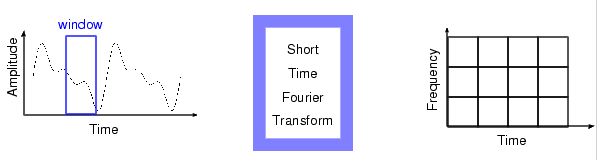
STFT представляет своего рода компромисс между временем - и основанными на частоте представлениями сигнала. Это предоставляет некоторую информацию и о том, когда и в том, какие частоты событие сигнала возникают. Однако можно только получить эту информацию с ограниченной точностью, и та точность определяется размером окна.

В то время как компромисс STFT между временем и информацией о частоте может быть полезным, недостаток то, что, если вы выбираете конкретный размер для окна времени, что окно является тем же самым для всех частот. Много сигналов требуют более гибкого подхода - тот, где можно отличаться размер окна, чтобы определить более точно или время или частоту.

Вместо того, чтобы строить STFT в трех измерениях, соглашение состоит в том, чтобы закодировать $| F (ω, τ) |$ как интенсивность на некоторой карте цветов. Вычисление и отображение STFT двух синусоид на 20 Гц различной длительности, показанной ранее:

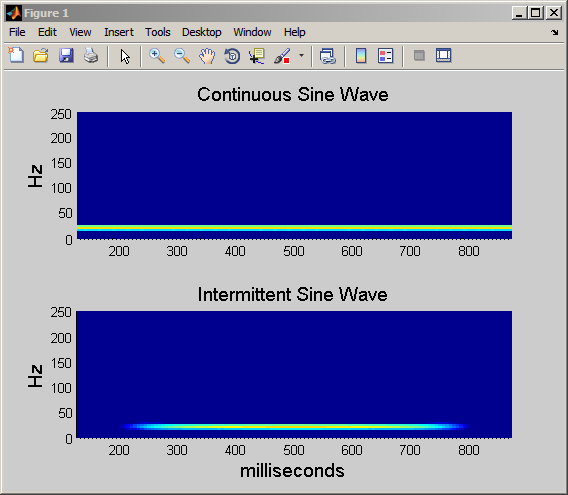
При помощи STFT вы видите, что неустойчивая синусоида начинает близкие 250 мс и заканчивает приблизительно 750 мс. Кроме того, вы видите, что энергия сигнала сконцентрирована приблизительно 20 Гц.

Документация