Этот раздел берет вас через функции Нового Вейвлета для CWT, один из Wavelet Toolbox™ специализировал инструменты.
Тулбокс требует, чтобы только одна функция разработала новый вейвлет, адаптированный к данному шаблону к CWT: pat2cwav. Вы найдете полную информацию об этой функции на ее странице с описанием.
В этом разделе вы будете учиться как
Загрузите шаблон
Синтезируйте новый вейвлет, адаптированный к данному шаблону
Выявите закономерности CWT с помощью адаптированного вейвлета
Сравните обнаружение с помощью и адаптированного вейвлета и известных вейвлетов
Сохраните синтезируемый вейвлет
Поскольку можно выполнить проект нового вейвлета для CWT или из командной строки или из использования приложения Wavelet Analyzer, этот раздел имеет подразделы, покрывающие каждый метод.
Принцип для разработки нового вейвлета для CWT должен аппроксимировать данный шаблон с помощью оптимизации наименьших квадратов при ограничительном продвижении к допустимому вейвлету, которому хорошо удовлетворяют для обнаружения шаблона с помощью непрерывного вейвлета, преобразовывают (см. [MisMOP03] в Ссылках).
Этот пример иллюстрирует, как сгенерировать новый вейвлет, начинающий с шаблона.
Загрузите исходный шаблон: псевдо синус.
load ptpssin1
whoYour variables are: IntVAL X Y caption
Переменные X и Y содержат шаблон. Интегрируйте шаблон на интервале [0, 1]. Постройте шаблон.
dX = max(diff(X));
patternInt = dX*sum(Y);
disp(['Integral of pattern = ',num2str(patternInt)]);Integral of pattern = 0.15915
plot(X,Y) title('Original Pattern') grid on

Шаблон на интервале [0, 1] объединяется к 0,15915. Таким образом, это не вейвлет, но это - хороший кандидат, поскольку это колеблется как вейвлет.
Чтобы синтезировать новый вейвлет, адаптированный к данному шаблону, используйте полиномиальное приближение наименьших квадратов степени 6 с ограничениями непрерывности вначале и конца шаблона.
[psi,xval,nc] = pat2cwav(Y, 'polynomial',6, 'continuous');
Новый вейвлет дан xval и nc*psi.
figure plot(X,Y,'-',xval,nc*psi,'--') grid on legend('Original Pattern','Adapted Wavelet','Location','NorthWest')

Чтобы использоваться в алгоритме CWT, новый вейвлет должен иметь квадратную норму, равную 1. Подтвердите, что новый вейвлет имеет квадратную норму, равную 1.
dxval = max(diff(xval));
newWaveletSqN = dxval*sum(psi.^2);
disp(['New wavelet has square norm = ',num2str(newWaveletSqN)])New wavelet has square norm = 1
Запустите новый вейвлет для инструмента CWT.
От подсказки MATLAB® введите waveletAnalyzer.
Wavelet Analyzer появляется. Кликните по пункту меню New Wavelet for CWT, чтобы отобразить Шаблон Адаптированный Допустимый Design Tool Вейвлета.
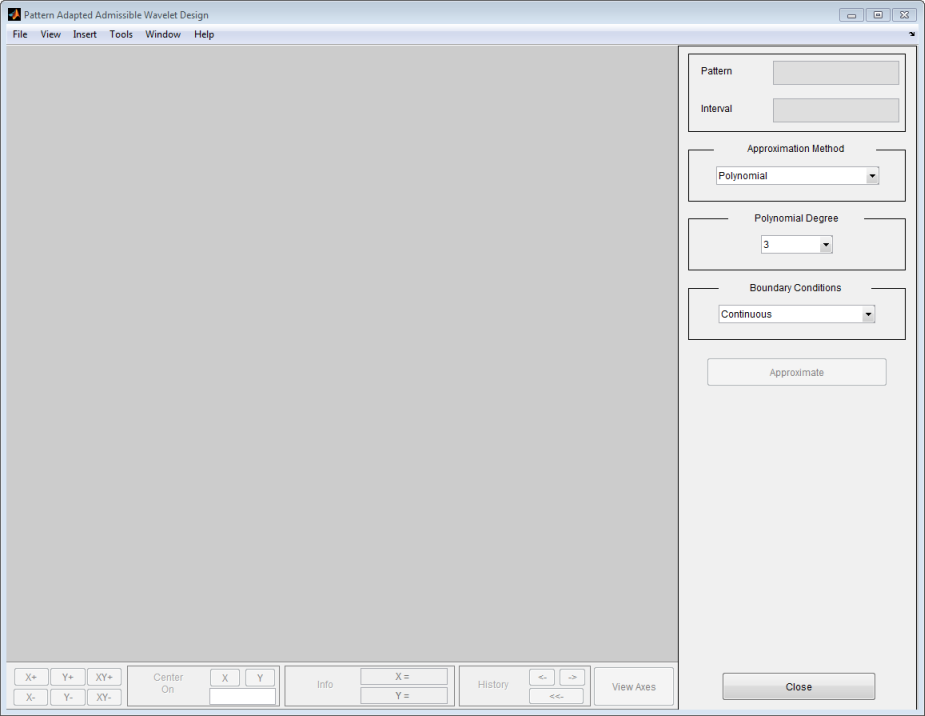
Загрузите исходный шаблон. В Шаблоне Адаптированный Допустимый Design Tool Вейвлета, из меню File, выбирают Load Pattern. Когда диалоговое окно Load Pattern появляется, перейдите к matlabroot/toolbox/wavelet/wavelet, где matlabroot является корневой папкой MATLAB. Выберите ptpssin1.mat. Кликните по кнопке OK.
MAT-файл, задающий шаблон, может содержать больше чем одну переменную. В этом случае переменная Y рассматривается, если она существует; в противном случае первая переменная рассматривается.
Выбранный шаблон, обозначенный F, задан на интервале [0,1] и интеграла 0.1592. Это не вейвлет, но это - хороший кандидат, потому что это колеблется как вейвлет.
Выполните приближение шаблона.
Примите, что продвижение параметров по умолчанию использует полином степени 3 с ограничениями непрерывности на границах 0 и 1, аппроксимирует шаблон F. Нажмите кнопку Approximate.
После паузы для вычисления инструмент отображает новый вейвлет зеленого цвета, наложенного с исходным шаблоном красного цвета.
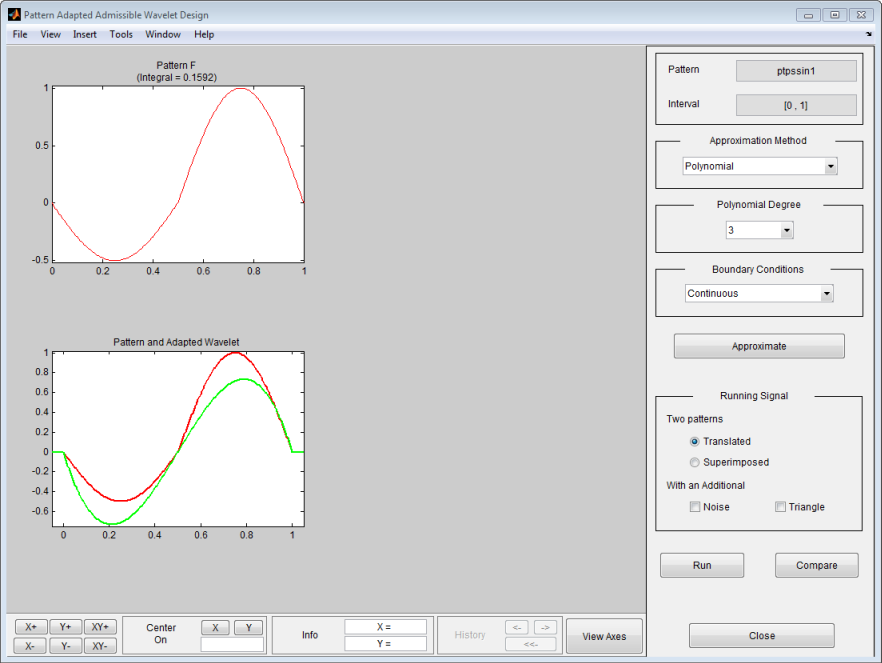
Результат не является действительно удовлетворительным. Решение состоит в том, чтобы увеличить полиномиальную степень, чтобы соответствовать лучше шаблону.
Используя меню Polynomial Degree, увеличьте степень путем выбора 6. Затем нажмите кнопку Approximate снова.
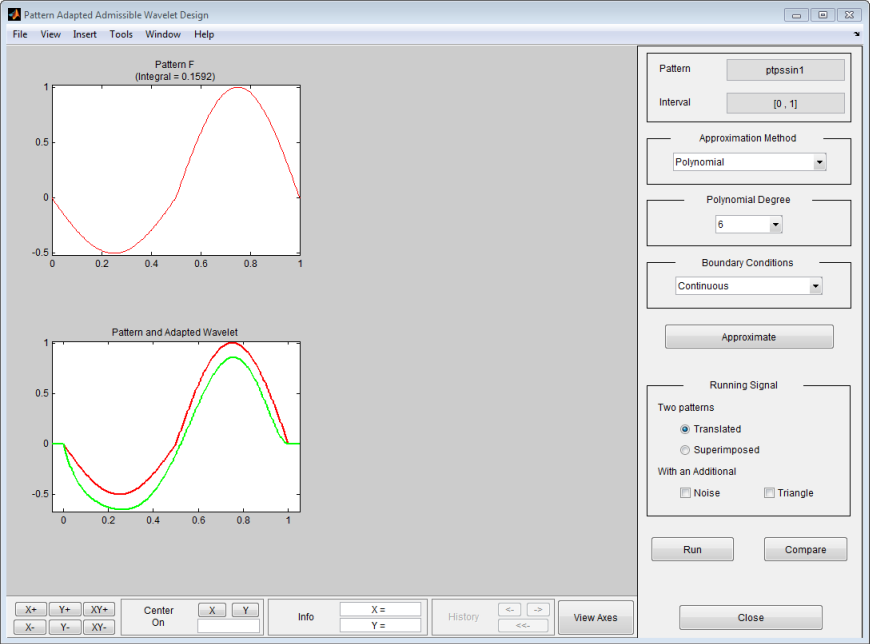
Результат теперь имеет хорошее качество и может использоваться для обнаружения шаблона.
Обнаружение шаблона с помощью нового вейвлета.
Щелкните по кнопке Run.
После паузы для вычисления инструмент отображает рабочий сигнал и обнаружение шаблона CWT с помощью адаптированного вейвлета.
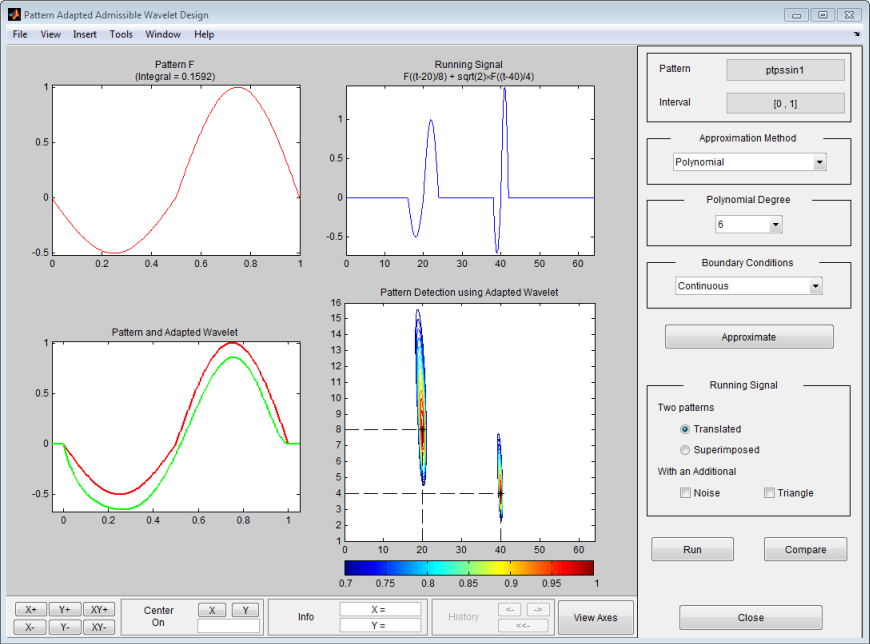
Рабочий сигнал является наложением двух расширенных и переведенных версий шаблона F, а именно, F((t-20)/8) и F((t-40)/4). Эти две пары (положение, шкала), чтобы быть обнаруженными даны (20,8) и (40,4) и осуществлены пунктирными линиями в нижнем правом графике контурного графика CWT. Обнаружение совершенно, потому что два локальных максимума абсолютных значений непрерывных коэффициентов вейвлета соответствуют отлично.
Используя Рабочий кадр сигнала, установите флажок Noise, чтобы добавить аддитивный шум в предыдущий сигнал. Щелкните по кнопке Run снова.
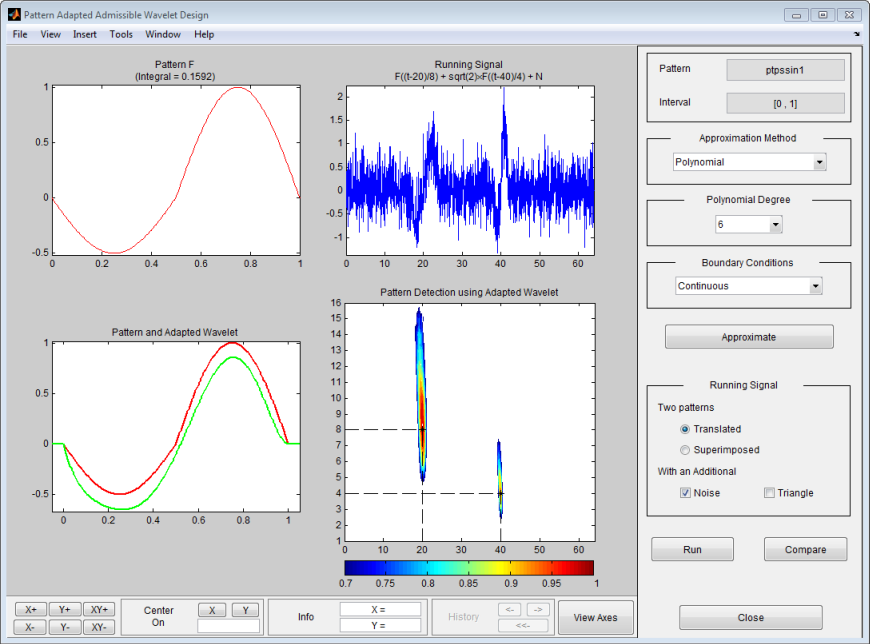
Качество обнаружения не изменено вообще.
Сравните адаптированный вейвлет и известные вейвлеты.
Давайте теперь сравним производительность для обнаружения шаблона адаптированного вейвлета по сравнению с известными вейвлетами. Кликните по Кнопке "Сравнить". Появляется новое окно.
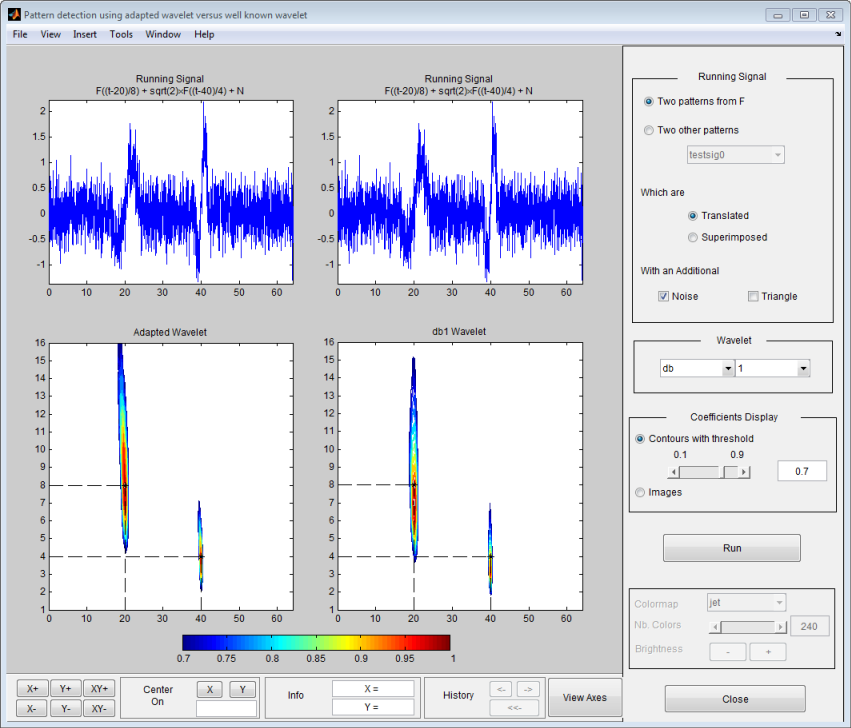
Этот инструмент отображает обнаружение шаблона, выполняемое с адаптированным вейвлетом слева и вейвлетом db1 (значение по умолчанию) справа. Эти два положения отлично обнаруживаются в обоих случаях, но шкалы немного недооценены вейвлетом db1.
Инструмент позволяет вам генерировать различные рабочие сигналы и выбирать вейвлет, чтобы быть по сравнению с адаптированным.
Нажмите кнопку Close, чтобы возвратиться к главному окну.
Новый Вейвлет для Инструмента CWT позволяет вам сохранить синтезируемый вейвлет. Тулбокс создает MAT-файл в текущей папке с именем, которое вы выбираете.
Чтобы избавить новый вейвлет от существующего выбора, используйте опцию Файл>, Сохраняют Адаптированный Вейвлет. Диалоговое окно появляется, который позволяет вам задать папку и имя файла для того, чтобы хранить данные. После того, как вы сохраните данные о вейвлете к файлу newwavel.mat, адаптированный вейвлет дан X и Y.
Обратите внимание на то, что версия сохраненного вейвлета правильно задана, чтобы использоваться в алгоритме CWT и такова, что его квадратная норма равна 1.