Шумоподавление мультисигнала 1-D с помощью вейвлетов
[XD,DECDEN,THRESH] = mswden('den',...)
[XD,THRESH] = mswden('densig',...)
[DECDEN,THRESH]
= mswden('dendec',...)
THRESH = mswden('thr',...)
[...] = mswden(OPTION,DIRDEC,X,WNAME,LEV,METH,PARAM)
[...] = mswden(...,S_OR_H)
[...]
= mswden(...,S_OR_H,KEEPAPP)
[...]
= mswden(...,S_OR_H,KEEPAPP,IDXSIG)
mswden вычисляет пороги и, в зависимости от выбранной опции, выполняет шумоподавление 1D сигналов с помощью вейвлетов.
[XD,DECDEN,THRESH] = mswden('den',...) возвращает denoised версию XD исходного матричного X мультисигнала, структурой разложения вейвлета которого является DEC. Вывод XD получен пороговой обработкой коэффициенты вейвлета, DECDEN является разложением вейвлета, сопоставленным к XD (см. mdwtdec), и THRESH является матрицей пороговых значений. Вход METH является именем метода шумоподавления, и PARAM является связанным параметром при необходимости.
Допустимые методы шумоподавления METH и сопоставленные параметры PARAM:
'rigrsure' | Принцип несмещенного риска глиняной кружки |
'heursure' | Эвристический вариант права преимущественной покупки |
'sqtwolog' | Универсальный порог |
'minimaxi' | Минимаксная пороговая обработка (см. |
Для этих методов PARAM задает мультипликативное пороговое перемасштабирование:
'one' | Никакое перемасштабирование |
'sln' | Перемасштабирование использования одной оценки шума уровня на основе первых коэффициентов уровня |
'mln' | Перемасштабирование использования зависимой оценки уровня шума уровня |
'penal' | Уголовный |
'penalhi' | Уголовный высокий, |
'penalme' | Уголовный носитель, |
'penallo' | Уголовный низкий, |
PARAM является параметром разреженности, и это должно быть таково что: 1 ≤ PARAM ≤ 10. Для метода penal не сделано никакое управление.
'man_thr' | Ручной метод |
PARAM является NbSIG-by-NbLEV матрица или NbSIG (NbLEV+1) матрицей, таким образом что:
PARAM(i,j) является порогом для коэффициентов детали уровня j для сигнала ith (1 ≤ j ≤ NbLEV).
PARAM(i,NbLEV+1) является порогом для коэффициентов приближения для i th сигнал (если KEEPAPP является 0).
где NbSIG является количеством сигналов и NbLEV количество уровней разложения.
Вместо входа 'den' OPTION можно использовать 'densig', 'dendec' или 'thr' OPTION, чтобы выбрать выходные аргументы:
[XD,THRESH] = mswden('densig',...) или [DECDEN,THRESH]
= mswden('dendec',...)
THRESH = mswden('thr',...) возвращает вычисленные пороги, но шумоподавление не выполняется.
Входной параметр структуры разложения DEC может быть заменен четырьмя аргументами: DIRDEC, X, WNAME и LEV.
[...] = mswden(OPTION,DIRDEC,X,WNAME,LEV,METH,PARAM) прежде, чем выполнить шумоподавление или вычислить пороги, матричный X мультисигнала анализируется на уровне LEV с помощью вейвлета WNAME в направлении DIRDEC.
Можно использовать еще три дополнительных входных параметров:
[...] = mswden(...,S_OR_H) или
[...]
= mswden(...,S_OR_H,KEEPAPP) или
[...]
= mswden(...,S_OR_H,KEEPAPP,IDXSIG)
S_OR_H ('s' or 'h') обозначает мягкую или трудную пороговую обработку (дополнительную информацию см. в mswthresh).
KEEPAPP (true or false) указывает, сохранить ли коэффициенты приближения (true) или не (false).
IDXSIG является вектором, который содержит индексы начальных сигналов или 'all'.
Значениями по умолчанию является, соответственно, 'h', false и 'all'.
% Load original 1D-multisignal.
load thinker
% Perform a decomposition at level 2 using the wavelet db2.
dec = mdwtdec('r',X,2,'db2');
% Denoise signals using the universal method
% of thresholding (sqtwolog) and the 'sln'
% threshold rescaling (with a single estimation
% of level noise, based on first level coefficients).
[XD,decDEN,THRESH] = mswden('den',dec,'sqtwolog','sln');
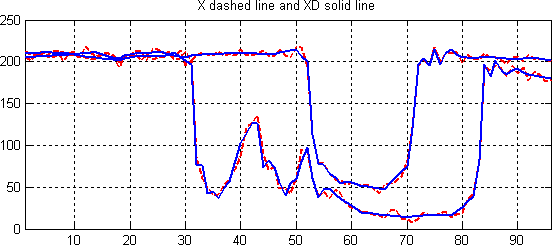
% Plot the original signals 1 and 31, and the
% corresponding denoised signals.
figure;
plot(X([1 31],:)','r--','linewidth',2); hold on
plot(XD([1 31],:)','b','linewidth',2);
grid; set(gca,'Xlim',[1,96])
title('X dashed line and XD solid line')
Birgé, Л.; П. Мэссарт (1997), “От образцового выбора до адаптивной оценки”, в Д. Полларде (редактор), Festchrift для Ль. Ле Кама, Спрингера, стр 55–88.
DeVore, Р.А.; Б. Джейрт, Б.Дж. Лукир (1992), “Сжатие изображения через вейвлет преобразовывает кодирование”, Сделка IEEE на Inf. Теория, издание 38, № 2, стр 719–746.
Donoho, D.L. (1993), “Прогресс анализа вейвлета и WVD: десятиминутный тур”, происходящий в анализе вейвлета и приложениях, И. Мейере. Роке, стр 109–128. Фронтиерес Эд.
Donoho, Д.Л.; И.М. Джонстон (1994), “Идеальная пространственная адаптация уменьшением вейвлета”, Biometrika, издание 81, стр 425–455.
Donoho, Д.Л.; И.М. Джонстон, Г. Керкьячариэн, Д. Пикар (1995), “Уменьшение вейвлета: asymptopia”, Подмастерье. Рой. Закон Soc.,series B, издание 57 № 2, стр 301–369.
Donoho, Д.Л.; И.М. Джонстон, “Идеальное шумоподавление в ортонормированном базисе, выбранном из библиотеки основ”, C.R.A.S. Париж, t. 319, Сер. Я, стр 1317–1322.
Donoho, D.L. (1995), “Шумоподавление мягкой пороговой обработкой”, Сделка IEEE на Inf. Теория, 41, 3, стр 613–627.