scal2frq

Масштабируйтесь к частоте

Синтаксис

F = scal2frq(A,'wname',DELTA) scal2frq(A,'wname') scal2frq(A,'wname',1)

Описание

F = scal2frq(A,'wname',DELTA) возвращает псевдочастоты, соответствующие шкалам, данным A и функцией вейвлета 'wname' (см. wavefun для получения дополнительной информации), и период выборки DELTA.

scal2frq(A,'wname') эквивалентно scal2frq(A,'wname',1).

Существует только аппроксимированный ответ для отношения между шкалой и частотой.

В анализе вейвлета способ связать шкалу с частотой состоит в том, чтобы определить центральную частоту вейвлета, _Fc, и использовать следующее отношение:

$F_{a} = \frac{F_{c}}{a}$

где

a является шкалой.
_Fc является центральной частотой вейвлета в Гц.
_Fa является псевдочастотой, соответствующей шкале a в Гц.

Идея состоит в том, чтобы сопоставить с данным вейвлетом чисто периодический сигнал частоты _Fc. Частотой, максимизирующей преобразование Фурье модуля вейвлета, является _Fc. centfrq вычисляет центральную частоту для заданного вейвлета. От вышеупомянутого отношения это видно, что шкала обратно пропорциональна псевдочастоте. Например, если шкала увеличивается, вейвлет становится более распространенным, приводя к более низкой псевдочастоте.

Некоторые примеры соответствия между центральной частотой и вейвлетом показывают в следующей фигуре.

Центральные частоты для действительных и комплексных вейвлетов

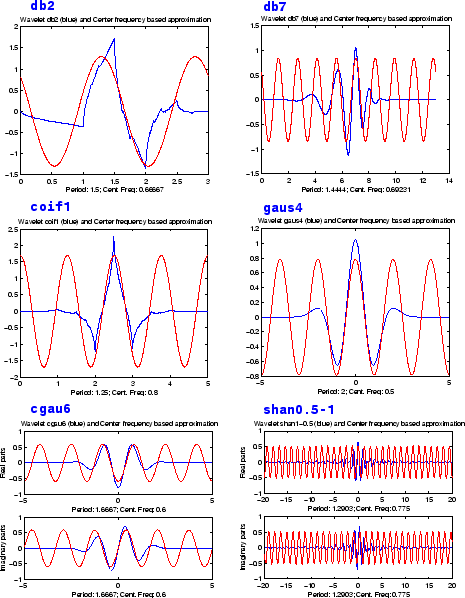
Как вы видите, центральное основанное на частоте приближение получает основные колебания вейвлета. Центральная частота является удобной и простой характеристикой доминирующей частоты вейвлета.

Примеры

свернуть все

Шкалы к частотам

Скрипт Open Live Script

Создайте вектор шкал с 10 речью на октаву более чем пять октав. Примите, что данные выбираются на уровне 10 кГц.

voicesperoctave = 10;
numoctaves = 5;
a0 = 2^(1/voicesperoctave);
Fs = 1e4;
scales = ...
    a0.^(voicesperoctave:numoctaves*voicesperoctave);

Преобразуйте шкалы, чтобы аппроксимировать частоты в герц для вейвлета Morlet.

Frq = scal2frq(scales,'morl',1/Fs);

Определите соответствующие периоды. Создайте таблицу со шкалами, соответствующими частотами и периодами. Отобразите самые маленькие 20 шкал наряду с их соответствующими частотами и периодами.

Frq = Frq(:);
scales = scales(:);
T = [scales.*(1/Fs) Frq 1./Frq];
T = array2table(T,'VariableNames',{'Scale','Frequency','Period'});
T(1:20,:)

ans=20×3 table
      Scale       Frequency      Period  
    __________    _________    __________

        0.0002     4062.5      0.00024615
    0.00021435     3790.4      0.00026382
    0.00022974     3536.6      0.00028276
    0.00024623     3299.8      0.00030305
     0.0002639     3078.8       0.0003248
    0.00028284     2872.6      0.00034811
    0.00030314     2680.3       0.0003731
     0.0003249     2500.8      0.00039988
    0.00034822     2333.3      0.00042858
    0.00037321       2177      0.00045934
        0.0004     2031.3      0.00049231
    0.00042871     1895.2      0.00052764
    0.00045948     1768.3      0.00056551
    0.00049246     1649.9       0.0006061
     0.0005278     1539.4       0.0006496
    0.00056569     1436.3      0.00069623
      ⋮

Постройте CWT с частотами в контурном графике

Скрипт Open Live Script

Пример показывает, как создать контурный график CWT с помощью аппроксимированных частот в Гц.

Создайте сигнал, состоящий из двух синусоид с непересекающейся поддержкой в аддитивном шуме. Примите, что сигнал выбирается на уровне 1 кГц.

Fs = 1000;
t = 0:1/Fs:1-1/Fs;
x = 1.5*cos(2*pi*100*t).*(t<0.25)+1.5*cos(2*pi*50*t).*(t>0.5 & t<=0.75);
x = x+0.05*randn(size(t));

Получите CWT входного сигнала и постройте результат.

[cfs,f] = cwt(x,Fs);
contour(t,f,abs(cfs).^2); 
axis tight;
grid on;
xlabel('Time');
ylabel('Approximate Frequency (Hz)');
title('CWT with Time vs Frequency');

Ссылки

Abry, P. (1997), Ondelettes и турбулентность. Multirésolutions, алгоритмы de décomposition, инвариантность d'échelles, Дидро Эдитер, Париж.

Смотрите также

centfrq

Документация