Вейвлет и масштабирующиеся функции
[PHI,PSI,XVAL] = wavefun('wname',ITER)
[PHI1,PSI1,PHI2,PSI2,XVAL] = wavefun('wname',ITER)
[PHI,PSI,XVAL] = wavefun('wname',ITER)
[PSI,XVAL] = wavefun('wname',ITER)
[...] = wavefun(wname,A,B)
[...] = wavefun('wname',max(A,B))
[...] = wavefun('wname',0)
[...] = wavefun('wname',8,0)
[...] = wavefun('wname')
[...] = wavefun('wname',8)
Функциональный wavefun возвращает приближения функции вейвлета 'wname' и связанная функция масштабирования, если это существует. Положительный целочисленный ITER определяет количество вычисленных итераций; таким образом, улучшение приближений.
Для ортогонального вейвлета:
[PHI,PSI,XVAL] = wavefun( возвращает масштабирование и функции вейвлета на сетке точек 'wname',ITER)XVAL.
Для биоортогонального вейвлета:
[PHI1,PSI1,PHI2,PSI2,XVAL] = wavefun( возвращает масштабирование и функции вейвлета и для разложения 'wname',ITER)(PHI1,PSI1) и для реконструкции (PHI2,PSI2).
Для вейвлета Мейера:
[PHI,PSI,XVAL] = wavefun('wname',ITER)
Для вейвлета, не масштабируя функцию (например, Morlet, мексиканская Шляпа, Гауссовы вейвлеты производных или комплексные вейвлеты):
[PSI,XVAL] = wavefun('wname',ITER)
[...] = wavefun(, то, где wname,A,B)A и B являются положительными целыми числами, эквивалентно [...] = wavefun(, и строит графики. 'wname',max(A,B))
Когда A установлен равный специальному значению 0,
[...] = wavefun( эквивалентно 'wname',0)
[...] = wavefun(.'wname',8,0)
[...] = wavefun( эквивалентно 'wname')
[...] = wavefun(.'wname',8)
Выходные аргументы являются дополнительными.
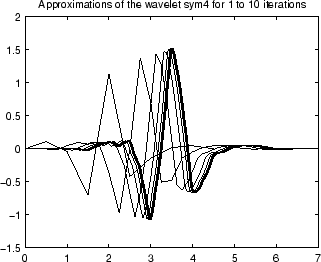
На следующем графике, 10 кусочных линейных аппроксимациях вейвлета sym4, полученного после каждой итерации каскадного алгоритма, показаны.
% Set number of iterations and wavelet name.
iter = 10;
wav = 'sym4';
% Compute approximations of the wavelet function using the
% cascade algorithm.
for i = 1:iter
[phi,psi,xval] = wavefun(wav,i);
plot(xval,psi);
hold on
end
title(['Approximations of the wavelet ',wav, ...
' for 1 to ',num2str(iter),' iterations']);
hold off
Для сжато поддерживаемых вейвлетов, заданных фильтрами, в целом никакая закрытая форма существует аналитическая формула.
Используемый алгоритм является каскадным алгоритмом. Это использует одноуровневый обратный вейвлет неоднократно, преобразовывают.
Давайте начнем с масштабирующейся функции ϕ.
Поскольку ϕ также равен ϕ0,0, эта функция характеризуется следующими коэффициентами в ортогональной среде:
<ϕ, ϕ0,n> = 1, только если n = 0 и равный 0 в противном случае
<ϕ, ψ−j,k> = 0 для положительного j и всего k.
Это расширение может быть просмотрено как структура разложения вейвлета. Коэффициенты детали являются всеми нулями, и коэффициенты приближения являются всеми нулями кроме одного равного 1.
Затем мы используем алгоритм реконструкции, чтобы аппроксимировать функцию ϕ по двухместной сетке, согласно следующему результату:
Для любого двухместного рациональный из формы x = n 2−j, в котором функция непрерывна и где j является достаточно большим, у нас есть pointwise сходимость и
![]()
где C является константой, и α является положительной константой в зависимости от регулярности вейвлета.
Затем с помощью хорошего приближения ϕ на двухместном rationals, мы можем использовать кусочные постоянные или кусочные линейные интерполяции η на двухместных интервалах, для которых равномерная сходимость происходит с подобным экспоненциальным уровнем:
![]()
Так с помощью J - схема реконструкции шага, мы получаем приближение, которое сходится экспоненциально к ϕ, когда J переходит к бесконечности.
Приближения вычисляются по сетке двухместного rationals покрытие поддержки функции, которая будет аппроксимирована.
Начиная с масштабированной версии функции вейвлета на ψ можно также подробно остановиться (ϕ−1, n)), n, та же схема может использоваться после одноуровневой реконструкции начиная с соответствующей структуры разложения вейвлета. Коэффициенты приближения являются всеми нулями и детализируют коэффициенты, все нули кроме одного равного 1.
Для биоортогональных вейвлетов те же идеи могут быть применены на каждую из двух схем мультиразрешения в дуальности.
Этот алгоритм может отличаться, если функция, которая будет аппроксимирована, не непрерывна на двухместном rationals.
Daubechies, я., Десять лекций по вейвлетам, CBMS, SIAM, 1992, стр 202Äì213.
Странг, Г.; Т. Нгуен (1996), вейвлеты и наборы фильтров, Wellesley-Кембриджское нажатие.