2D приложение непрерывного вейвлета преобразовывает (CWT) позволяет вам анализировать свои данные изображения и экспортировать результаты того анализа к рабочей области MATLAB®. Приложение обеспечивает всю функциональность функций командной строки cwtft2 и cwtftinfo2. Доступ к 2D приложению CWT в галерее приложений путем выбора Wavelet Design & Analysis в разделе Signal Processing and Communications или вводе
cwtfttool2
в подсказке команды MATLAB.
2D непрерывный вейвлет преобразовывает, представление 2D данных (данные изображения) в 4 переменных: расширение, вращение и положение. Расширение и вращение являются скалярами с действительным знаком, и положение является 2D вектором с элементами с действительным знаком. Позвольте x обозначить двухэлементный вектор вещественных чисел. Если
интегрируемо с квадратом на плоскости, 2D CWT задан как
где панель обозначает сопряженное комплексное число, и rθ является 2D матрицей вращения
2D CWT является масштабным изображением пробела изображения. Можно просмотреть инверсию шкалы и угла поворота, взятого вместе в качестве переменной пространственной частоты, которая дает 2D CWT интерпретацию как представление частоты пробела. Для всех допустимых 2D вейвлетов 2D CWT действует как локальный фильтр для изображения по своим масштабам и положения. Если вейвлет является изотропным, нет никакой зависимости от угла в анализе. Мексиканский вейвлет шляпы является примером изотропного вейвлета. Изотропные вейвлеты подходят для pointwise анализа изображений. Если вейвлет является анизотропным, существует зависимость от угла в анализе и 2D действиях CWT локальный фильтр для изображения по своим масштабам, положения и угла. Вейвлет Коши является примером анизотропного вейвлета. В области Фурье это означает, что пространственная поддержка частоты вейвлета является выпуклым конусом с вершиной в начале координат. Анизотропные вейвлеты подходят для обнаружения направленных функций в изображении. Смотрите Двумерный CWT Шумного Шаблона для рисунка различия между изотропными и анизотропными вейвлетами.
Этот пример показывает, как анализировать изображение с помощью 2D приложения CWT.
Загрузите треугольное изображение в рабочем пространстве MATLAB.
imdata = imread('triangle.jpg');Запустите 2D приложение CWT путем выбора Wavelet Design & Analysis в разделе Signal Processing and Communications галереи приложений. От раздела 2-D выберите Continuous Wavelet Transform 2-D. Также войдите
cwtfttool2
в подсказке команды MATLAB.
Выберите File –> Import Data, чтобы импортировать переменную imdata.
Из выпадающего меню Wavelet выберите вейвлет cauchy.
Для Angles и Scales, выберите опцию Manual.
Нажмите Define, чтобы задать вектор углов. Выберите Manual из Type выпадающий список и задайте вектор углов от 0 до радианов 7*pi/8 с шагом радианов pi/8, 0:pi/8:(7*pi)/8. Нажмите Apply, чтобы применить ваш выбор углов.
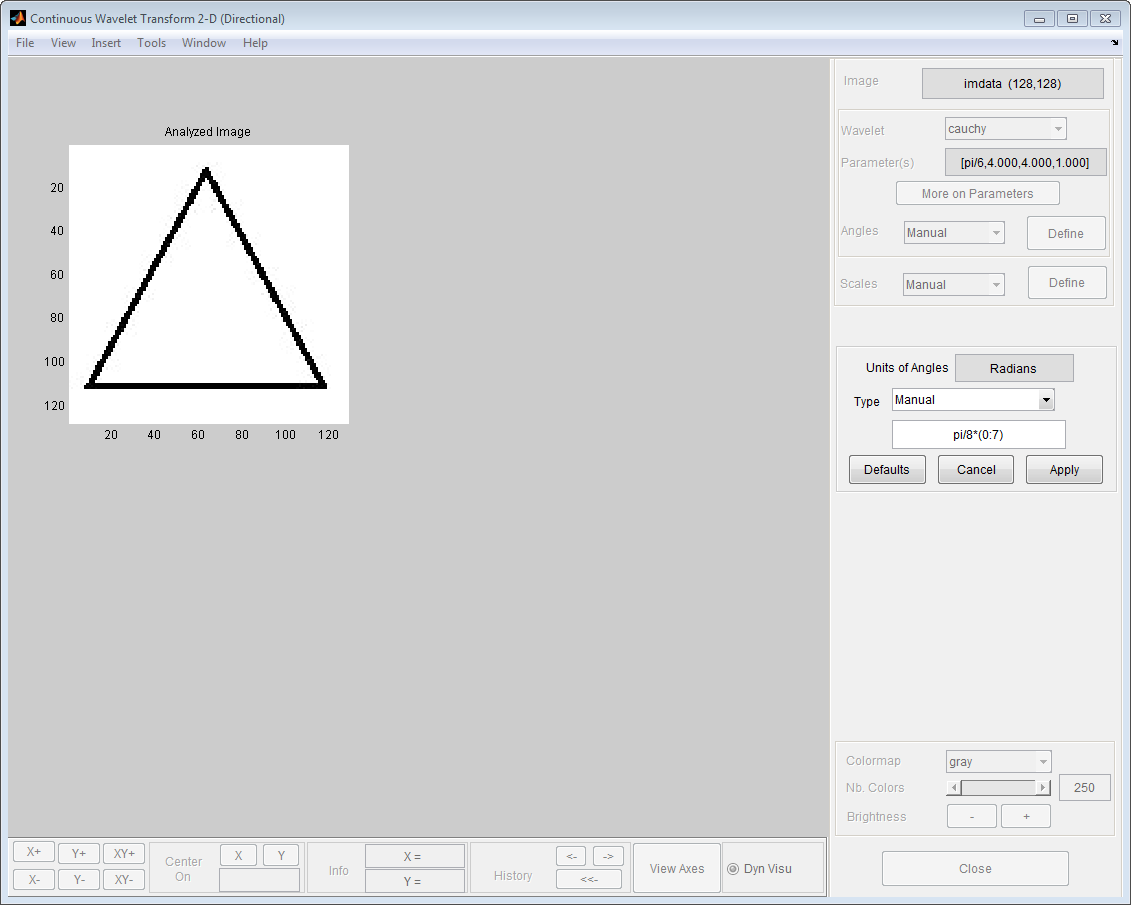
Нажмите Define, чтобы задать вектор шкал от 0,5 до 4 с шагом 0,5. Выберите Linear из Type выпадающий список. Установите First Scale, равный 0,5, Gap between two scales, равный 0,5, и Number of Scales, равный 8. Эквивалентно, можно выбрать Manual из Type выпадающий список и задать вектор шкал как 0.5:0.5:4. Нажмите Apply, чтобы применить ваш выбор шкал.
Нажмите Analyze, чтобы получить 2D CWT.
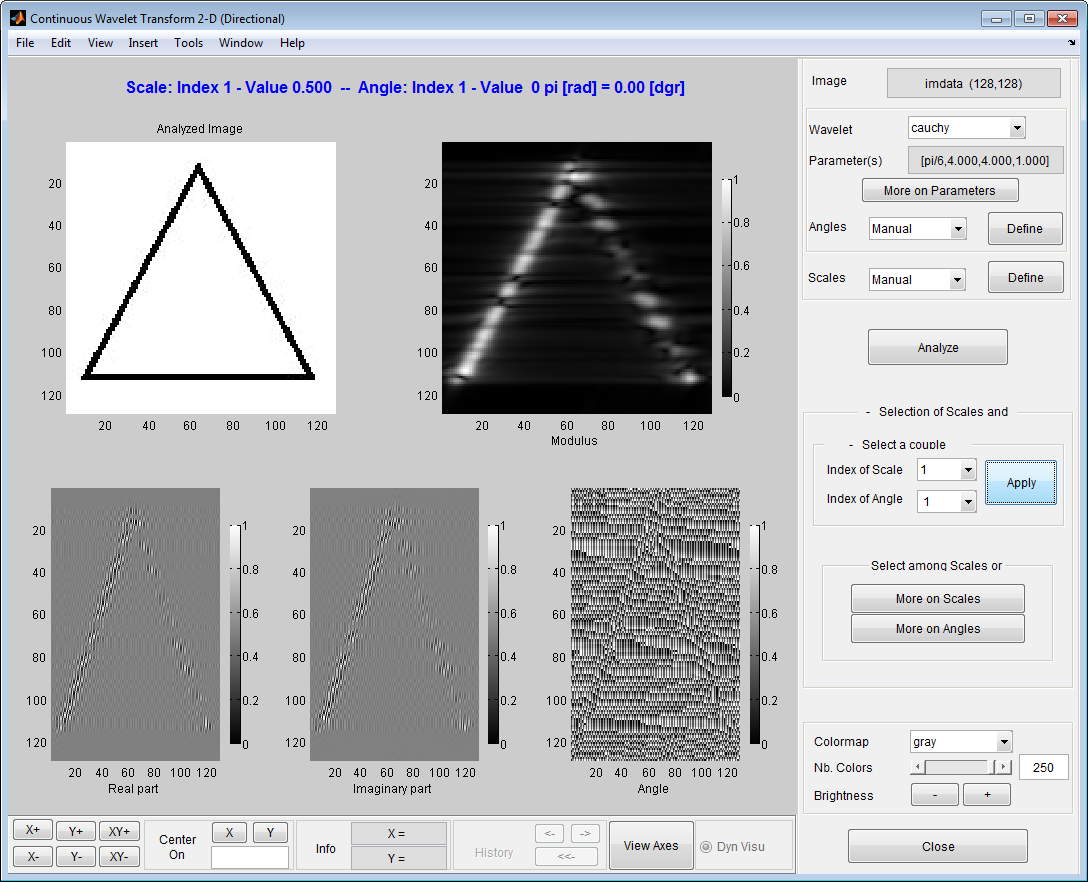
Установите Index of Scale быть 1 и нажимать More on Angles. Нажмите Movie, чтобы продвинуться через вручную заданные углы для 2D коэффициентов CWT в шкале 0.5.
Выберите File –> Export Data –> Export CWTFT Struct to Workspace, чтобы экспортировать анализ в рабочее пространство MATLAB. Можно найти объяснение полей структуры в ссылке на функцию для cwtft2.