Этот раздел демонстрирует функции многомерного шумоподавления, обеспеченного в программном обеспечении Wavelet Toolbox™. Тулбокс включает функцию wmulden и приложение Wavelet Analyzer. Этот раздел также описывает командную строку и методы приложения и включает информацию о передаче сигнала и информации о параметре между диском и приложением.
Эта многомерная проблема шумоподавления вейвлета имеет дело с моделями формы X (t) = F (t) + e (t), где наблюдение, X является p - размерный, F, является детерминированным сигналом, который будет восстановлен, и e является пространственно коррелированым шумовым сигналом. Этот вид модели хорошо подходит для ситуаций, для которых такое дополнение, пространственно коррелированый шум реалистичен.
Этот пример использует шумные тестовые сигналы. В этом разделе вы будете
Загрузите многомерный сигнал.
Отобразите исходные и наблюдаемые сигналы.
Удалите шум простой многомерной пороговой обработкой после изменения основания.
Отобразите сигналы denoised и оригинал.
Улучшите полученный результат путем сохранения меньшего количества основных компонентов.
Отобразите количество сохраненных основных компонентов.
Отобразите предполагаемую шумовую ковариационную матрицу.
Загрузите многомерный сигнал путем ввода следующего в подсказке MATLAB®:
load ex4mwden whos
| Имя | Размер | Байты | Класс |
|---|---|---|---|
covar | 4x4 | 128 | double array |
x | 1024x4 | 32768 | double array |
x_orig | 1024x4 | 32768 | double array |
Обычно, только матрица данных x доступна. Здесь, у нас также есть истинная шумовая ковариационная матрица (covar) и исходные сигналы (x_orig). Эти сигналы являются шумными версиями простых комбинаций двух исходных сигналов. Первый является “Блоками”, который неправилен, и вторым является “HeavySine”, который является регулярным приблизительно кроме времени 750. Другие два сигнала являются суммой и различием двух исходных сигналов. Многомерный Гауссов белый шум, показывающий сильную пространственную корреляцию, добавляется к получившимся четырем сигналам, который приводит к наблюдаемым данным, хранимым в x.
Отобразите исходные и наблюдаемые сигналы путем ввода
kp = 0;
for i = 1:4
subplot(4,2,kp+1), plot(x_orig(:,i)); axis tight;
title(['Original signal ',num2str(i)])
subplot(4,2,kp+2), plot(x(:,i)); axis tight;
title(['Observed signal ',num2str(i)])
kp = kp + 2;
end
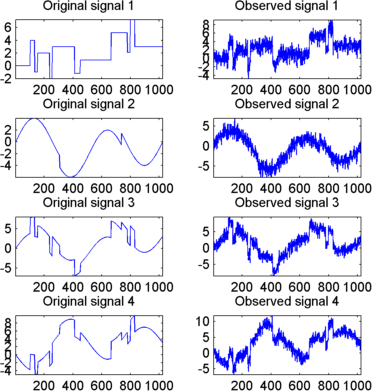
Истинной шумовой ковариационной матрицей дают
covar
covar =
1.0000 0.8000 0.6000 0.7000
0.8000 1.0000 0.5000 0.6000
0.6000 0.5000 1.0000 0.7000
0.7000 0.6000 0.7000 1.0000
Удалите шум простой многомерной пороговой обработкой.
Стратегия шумоподавления комбинирует одномерное шумоподавление вейвлета в основании, где предполагаемая шумовая ковариационная матрица является диагональной с Анализом главных компонентов (PCA) нев центре приближений в области вейвлета или с итоговым PCA.
Во-первых, выполните одномерное шумоподавление путем ввода следующего, чтобы установить параметры шумоподавления:
level = 5; wname = 'sym4'; tptr = 'sqtwolog'; sorh = 's';
Затем установите параметры PCA путем сохранения всех основных компонентов:
npc_app = 4; npc_fin = 4;
Наконец, выполните многомерное шумоподавление путем ввода
x_den = wmulden(x, level, wname, npc_app, npc_fin, tptr, sorh);
Отобразите оригинал и сигналы denoised путем ввода
kp = 0;
for i = 1:4
subplot(4,3,kp+1), plot(x_orig(:,i));
set(gca,'xtick',[]); axis tight;
title(['Original signal ',num2str(i)])
subplot(4,3,kp+2), plot(x(:,i)); set(gca,'xtick',[]);
axis tight;
title(['Observed signal ',num2str(i)])
subplot(4,3,kp+3), plot(x_den(:,i)); set(gca,'xtick',[]);
axis tight;
title(['denoised signal ',num2str(i)])
kp = kp + 3;
end
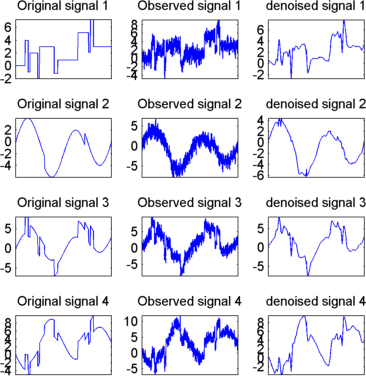
Улучшите первый результат путем сохранения меньшего количества основных компонентов.
Результаты являются удовлетворительными. При фокусировке на двух первых сигналах обратите внимание, что они правильно восстанавливаются, но результат может быть улучшен путем использования в своих интересах отношений между сигналами, продвижения к дополнительному эффекту шумоподавления.
Чтобы автоматически выбрать количества сохраненных основных компонентов по правилу Кайзера (который сохраняет компоненты сопоставленными с собственными значениями, превышающими среднее значение всех собственных значений), ввести
npc_app = 'kais'; npc_fin = 'kais';
Выполните многомерное шумоподавление снова путем ввода
[x_den, npc, nestco] = wmulden(x, level, wname, npc_app, ...
npc_fin, tptr, sorh);
Отобразите количество сохраненных основных компонентов.
Второй выходной аргумент дает количества сохраненных основных компонентов для PCA для приближений и для итогового PCA.
npc
npc =
2 2
Как ожидалось, поскольку сигналы являются комбинациями из двух начальных единиц, правило Кайзера автоматически обнаруживает, что только два основных компонента представляют интерес.
Отобразите предполагаемую шумовую ковариационную матрицу.
Третий выходной аргумент содержит предполагаемую шумовую ковариационную матрицу:
nestco
nestco =
1.0784 0.8333 0.6878 0.8141
0.8333 1.0025 0.5275 0.6814
0.6878 0.5275 1.0501 0.7734
0.8141 0.6814 0.7734 1.0967
Как вы видите путем сравнения истинному матричному покрытию, данному ранее, оценка является удовлетворительной.
Отобразите исходные и итоговые сигналы denoised путем ввода
kp = 0;
for i = 1:4
subplot(4,3,kp+1), plot(x_orig(:,i));
set(gca,'xtick',[]); axis tight;
title(['Original signal ',num2str(i)]); set(gca,'xtick',[]);
axis tight;
subplot(4,3,kp+2), plot(x(:,i)); set(gca,'xtick',[]);
axis tight;
title(['Observed signal ',num2str(i)])
subplot(4,3,kp+3), plot(x_den(:,i)); set(gca,'xtick',[]);
axis tight;
title(['denoised signal ',num2str(i)])
kp = kp + 3;
end
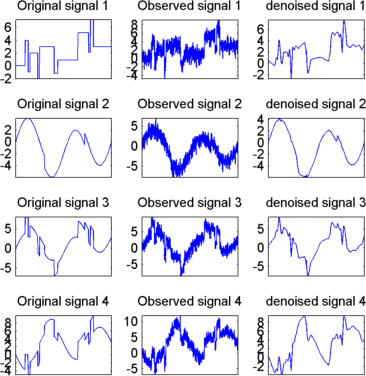
Результаты лучше, чем ранее полученные. Первый сигнал, который неправилен, все еще правильно восстанавливается, в то время как второй сигнал, который является более регулярным, является denoised лучше после этого второго этапа PCA.
Этот раздел исследует стратегию шумоподавления многомерных сигналов с помощью приложения Wavelet Analyzer.
Начните Многомерный Инструмент Шумоподавления первым открытием приложение Wavelet Analyzer. Введите waveletAnalyzer в командной строке.
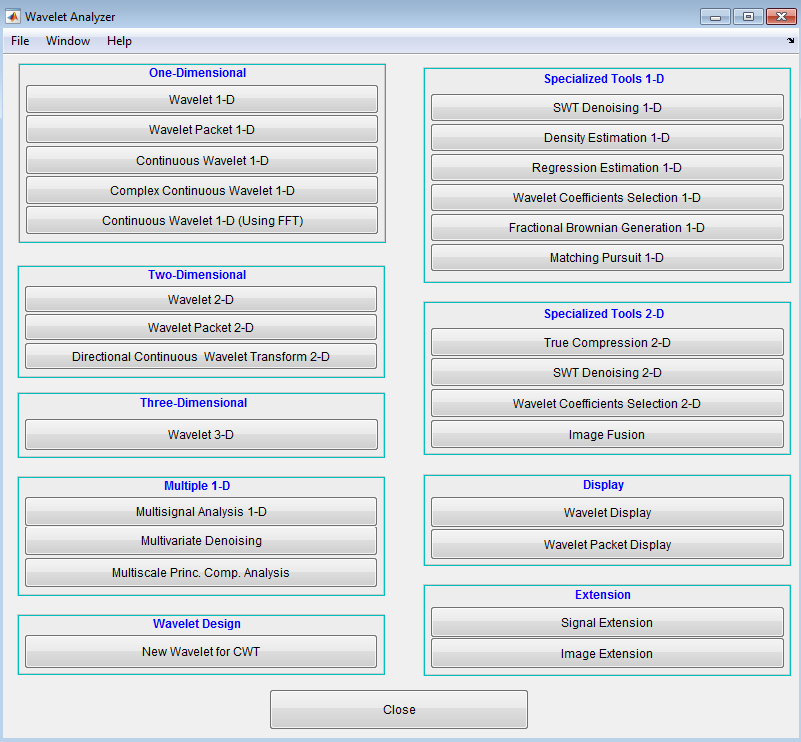
Нажмите Multivariate Denoising, чтобы открыть Многомерный фрагмент Шумоподавления приложения.
Загрузка данных.
В подсказке команды MATLAB ввести
load ex4mwden
x. Нажмите ОК, чтобы импортировать шумный многомерный сигнал. Сигнал является матрицей, содержащей четыре столбца, где каждый столбец является сигналом быть denoised.
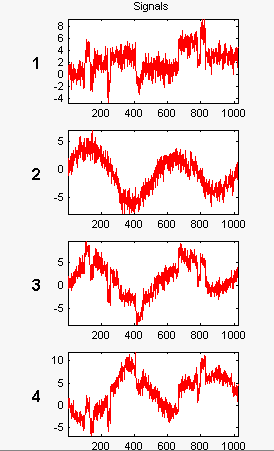
Эти сигналы являются шумными версиями от простых комбинаций двух исходных сигналов. Первый является “Блоками”, который неправилен, и вторым является “HeavySine”, который является регулярным приблизительно кроме времени 750. Другие два сигнала являются суммой и различием между исходными сигналами. Многомерный Гауссов белый шум, показывающий сильную пространственную корреляцию, добавляется к получившимся четырем сигналам.
Следующий пример иллюстрирует два различных аспекта предложенного метода шумоподавления. Во-первых, выполните удобное изменение основания, чтобы справиться с пространственной корреляцией и denoise в новом основании. Затем используйте PCA, чтобы использовать в своих интересах отношения между сигналами, ведя к дополнительному эффекту шумоподавления.
Выполните разложение вейвлета и diagonalize шумовая ковариационная матрица.
Используйте отображенные значения по умолчанию для Вейвлета, Дополнительного Режима DWT и Уровня разложения, и затем нажмите Decompose и Diagonalize. Инструмент отображает приближение вейвлета и коэффициенты детали разложения каждого сигнала в исходном основании.
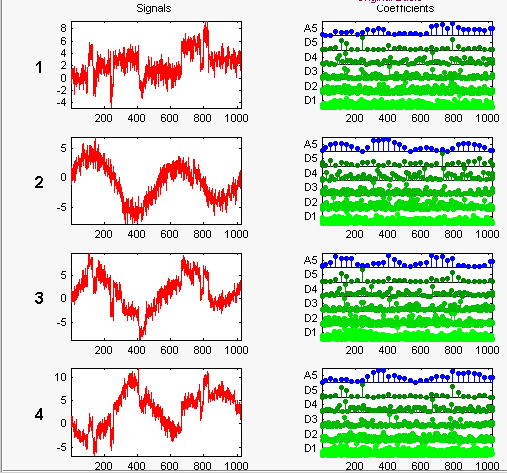
Выберите Noise Adapted Basis, чтобы отобразить сигналы и их коэффициенты в адаптированном к шуму основании.
Чтобы видеть больше информации об этом новом основании, нажмите More on Noise Adapted Basis. Новая фигура отображает устойчивую шумовую оценочную матрицу ковариации и соответствующие собственные вектора и собственные значения.
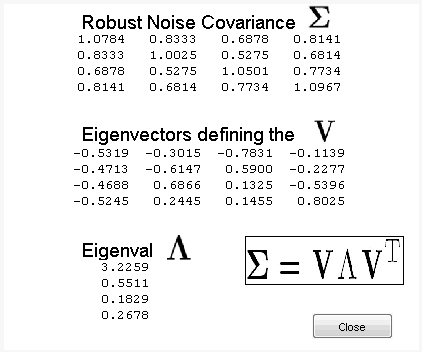
Собственные вектора задают изменение основания, и собственные значения являются отклонениями некоррелированых шумов в новом основании.
Многомерный метод шумоподавления, предложенный ниже, интересен, если шумовая ковариационная матрица далека от диагональной показывающей пространственной корреляции, которая, в этом примере, имеет место.
denoise многомерный сигнал.
Много опций доступны для подстройки алгоритма шумоподавления. Однако мы будем использовать значения по умолчанию: фиксированная форма мягкая пороговая обработка, масштабируемая белая шумовая модель и предложенные количества сохраненных основных компонентов. В этом случае значения по умолчанию для PCA приводят к сохранению всех компонентов.
Выберите Original Basis, чтобы возвратиться к исходному основанию и затем нажать Denoise.
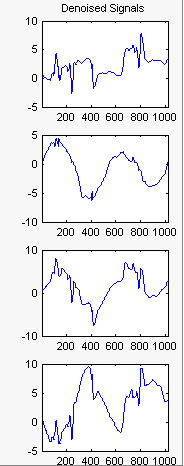
Результаты являются удовлетворительными. Оба из двух первых сигналов правильно восстанавливаются, но они могут быть улучшены путем получения большей информации об основных компонентах. Нажмите More on Principal Components.
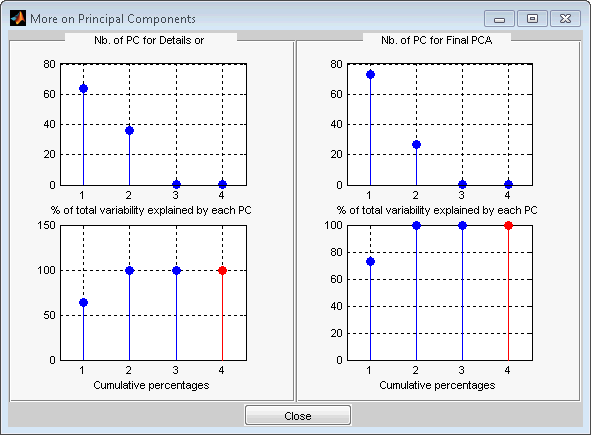
Новая фигура отображает информацию, чтобы выбрать количества компонентов, чтобы сохранить для PCA приближений и для итогового PCA после возвращения к исходному основанию. Вы видите проценты изменчивости, объясненной каждым основным компонентом и соответствующим кумулятивным графиком. Здесь, ясно, что только два основных компонента представляют интерес.
Закройте окно More on Principal Components. Выберите 2 как Nb. PC для APP. Выберите 2 как Nb. PC для итогового PCA, и затем кликните по denoise.
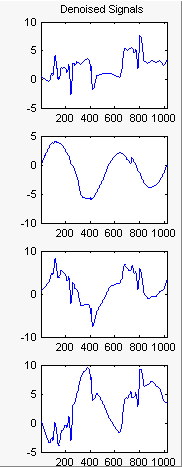
Результаты лучше, чем ранее полученные. Первый сигнал, который неправилен, все еще правильно восстанавливается. Второй сигнал, который является более регулярным, является denoised лучше после этого второго этапа PCA. Можно получить больше информации путем нажатия на Residuals.
Инструмент позволяет вам сохранить сигналы denoised на диск путем создания MAT-файла в текущей папке с именем по вашему выбору.
Сохранить сигнал denoised в предыдущем разделе,
Выберите File> Save denoised Сигналы.
Выберите Save denoised Сигналы и Параметры. Диалоговое окно появляется, который позволяет вам задать папку и имя файла для хранения сигнала.
Введите имя s_ex4mwden и нажмите ОК, чтобы сохранить данные.
Загрузите переменные в свою рабочую область:
load s_ex4mwdent whos
| Имя | Размер | Байты | Класс |
|---|---|---|---|
DEN_Params | 1x1 | 430 | struct array |
PCA_Params | 1x1 | 1536 | struct array |
x | 1024x4 | 32768 | struct array |
Сигналы denoised находятся в матричном x. Параметры (PCA_Params и DEN_Params) процесса шумоподавления 2D этапа также доступны.
PCA_Params являются изменением основания и параметров PCA:
PCA_Params
PCA_Params =
NEST: {[4x4 double] [4x1 double] [4x4 double]}
APP: {[4x4 double] [4x1 double] [2]}
FIN: {[4x4 double] [4x1 double] [2]}
PCA_Params.NEST{1} содержит изменение базисной матрицы. PCA_Params.NEST{2} содержит собственные значения, и PCA_Params.NEST{3} является предполагаемой шумовой ковариационной матрицей.
PCA_Params.APP{1} содержит изменение базисной матрицы, PCA_Params.APP{2} содержит собственные значения, и PCA_Params.APP{3} является количеством сохраненных основных компонентов для приближений.
Та же структура используется для PCA_Params.FIN для итогового PCA.
DEN_Params является параметрами шумоподавления в диагональном основании:
DEN_Params
DEN_Params =
thrVAL: [4.8445 2.0024 1.1536 1.3957 0]
thrMETH: 'sqtwolog'
thrTYPE: 's'
Пороги закодированы в thrVAL. Для j от 1 до 5 thrVAL(j) содержит значение, используемое к порогу коэффициенты детали на уровне j. Метод задания порога дан thrMETH, и режим пороговой обработки дан thrTYPE.