Этот раздел демонстрирует функции многошкального анализа основных компонентов, обеспеченного в программном обеспечении Wavelet Toolbox™. Тулбокс включает функцию wmspca и приложение Wavelet Analyzer. В этом разделе описываются командную строку и методы приложения и информацию о передаче сигнала и информации о параметре между диском и приложением.
Цель многошкального PCA состоит в том, чтобы восстановить, начинающий с многомерного сигнала и использующий простое представление на каждом уровне разрешения, упрощенном многомерном сигнале. Многошкальные основные компоненты обобщают нормальный PCA многомерного сигнала, представленного как матрица путем выполнения PCA на матрицах деталей разных уровней одновременно. PCA также выполняется на более грубой содействующей матрице приближения в области вейвлета, а также на финале восстановленная матрица. Путем выбора количеств сохраненных основных компонентов могут быть восстановлены интересные упрощенные сигналы.
Поскольку можно выполнить многошкальный PCA или из командной строки или из использования приложения, этот раздел имеет подразделы, покрывающие каждый метод.
Этот пример использует шумные тестовые сигналы. В этом разделе вы будете:
Загрузите многомерный сигнал.
Выполните простой многошкальный PCA.
Отобразите исходные и упрощенные сигналы.
Улучшите полученный результат путем сохранения меньшего количества основных компонентов.
Загрузите многомерный сигнал путем ввода в подсказке MATLAB®:
load ex4mwden whos
| Имя | Размер | Байты | Класс |
|---|---|---|---|
covar | 4x4 | 128 | double array |
x | 1024x4 | 32768 | double array |
x_orig | 1024x4 | 32768 | double array |
Данные, хранимые в матричном x, прибывают из двух тестовых сигналов, Блоков и HeavySine, и из их суммы и различия, к которому был добавлен многомерный Гауссов белый шум.
Выполните простой многошкальный PCA.
Многошкальные объединения PCA несосредоточенный PCA на приближениях и деталях в области вейвлета и итоговый PCA. На каждом уровне выбраны старшие значащие основные компоненты.
Во-первых, установите параметры вейвлета:
level= 5; wname = 'sym4';
Затем автоматически выберите количество сохраненных основных компонентов, использующих правило Кайзера путем ввода
npc = 'kais';
Наконец, выполните многошкальный PCA:
[x_sim, qual, npc] = wmspca(x ,level, wname, npc);
Отобразите исходные и упрощенные сигналы:
kp = 0;
for i = 1:4
subplot(4,2,kp+1), plot(x (:,i)); set(gca,'xtick',[]);
axis tight;
title(['Original signal ',num2str(i)])
subplot(4,2,kp+2), plot(x_sim(:,i)); set(gca,'xtick',[]);
axis tight;
title(['Simplified signal ',num2str(i)])
kp = kp + 2;
end
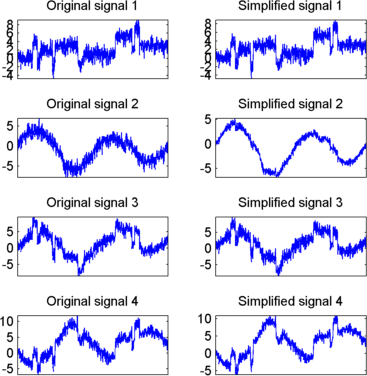
Результаты перспективы сжатия хороши. Проценты, отражающие качество реконструкций столбца, данных относительными среднеквадратичными погрешностями, близко к 100%.
qual qual = 98.0545 93.2807 97.1172 98.8603
Улучшите первый результат путем сохранения меньшего количества основных компонентов.
Результаты могут быть улучшены путем подавления шума, потому что детали на уровнях 1 - 3 составлены по существу шума с маленькими вкладами от сигнала. Удаление шума приводит к сырой нефти, но большой, эффект шумоподавления.
Выходной аргумент npc содержит количества сохраненных основных компонентов, выбранных правилом Кайзера:
npc
npc =
1 1 1 1 1 2 2
Для d от 1 до 5, npc(d) является количеством сохраненных основных компонентов нев центре (PC) для деталей на уровне d. Количеством сохраненных PC нев центре для приближений на уровне 5 является npc(6), и npc(7) является количеством сохраненных PC для итогового PCA после реконструкции вейвлета. Как ожидалось правило сохраняет два основных компонента, и для приближений PCA и для итогового PCA, но один основной компонент сохранен для деталей на каждом уровне.
Чтобы подавить детали на уровнях 1 - 3, обновите аргумент npc можно следующим образом:
npc(1:3) = zeros(1,3); npc npc = 0 0 0 1 1 2 2
Затем выполните многошкальный PCA снова:
[x_sim, qual, npc] = wmspca(x, level, wname, npc);
Отобразите исходные и итоговые упрощенные сигналы:
kp = 0;
for i = 1:4
subplot(4,2,kp+1), plot(x (:,i)); set(gca,'xtick',[]);
axis tight;
title(['Original signal ',num2str(i)]); set(gca,'xtick',[]);
axis tight;
subplot(4,2,kp+2), plot(x_sim(:,i)); set(gca,'xtick',[]);
axis tight;
title(['Simplified signal ',num2str(i)])
kp = kp + 2;
end
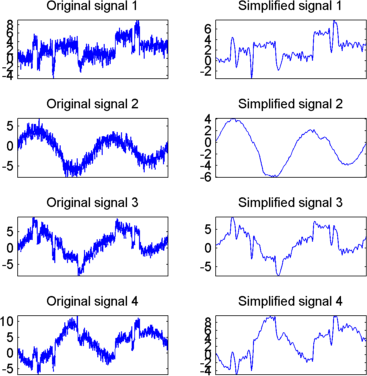
Как показано результаты улучшены.
Этот раздел исследует многошкальный PCA использование приложения Wavelet Analyzer.
Откройте приложение Wavelet Analyzer путем ввода waveletAnalyzer в командной строке.
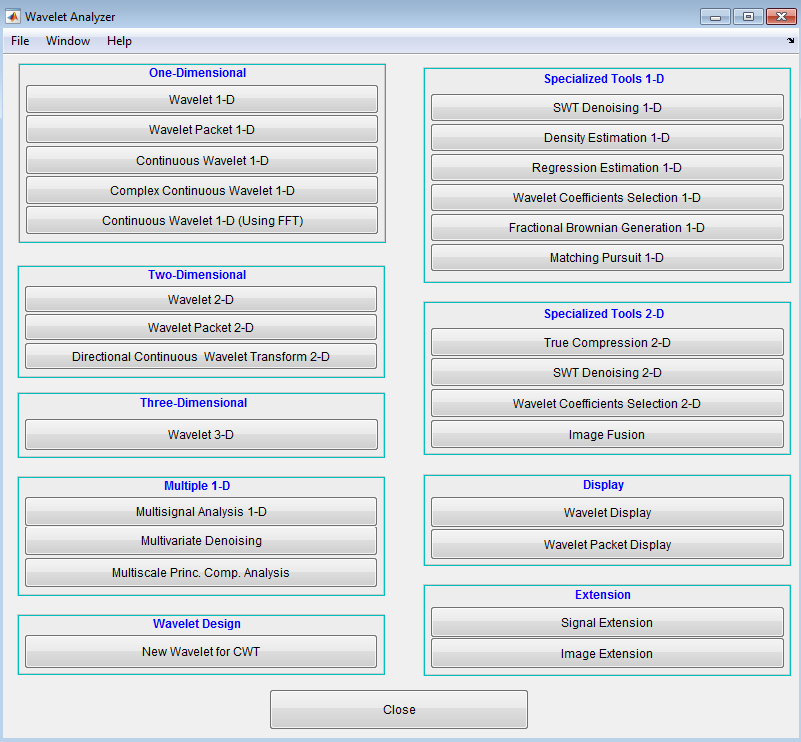
Нажмите Multiscale Princ. Аккомпанемент. Анализ, чтобы открыть инструмент Multiscale Principal Components Analysis в приложении.
Загрузка данных.
В подсказке команды MATLAB ввести
load ex4mwden
x. Нажмите ОК, чтобы импортировать многомерный сигнал. Сигнал является матрицей, содержащей четыре столбца, где каждый столбец является сигналом, который будет упрощен.
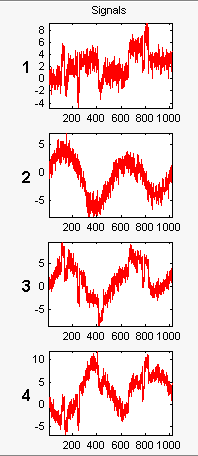
Эти сигналы являются шумными версиями от простых комбинаций двух исходных сигналов, Блоков и HeavySine и их суммы и различия, каждого с добавленным многомерным Гауссовым белым шумом.
Выполните разложение вейвлета и diagonalize каждая содействующая матрица.
Используйте значения по умолчанию для Вейвлета, Дополнительного Режима DWT и Уровня разложения, и затем нажмите Decompose и Diagonalize. Инструмент отображает приближение вейвлета и коэффициенты детали разложения каждого сигнала в исходном основании.
Чтобы получить больше информации о новых основах, допускавших, выполняя PCA для каждой шкалы, нажмите More on Adapted Basis. Новая фигура отображает соответствующие собственные вектора и собственные значения для матрицы коэффициентов детали на уровне 1.
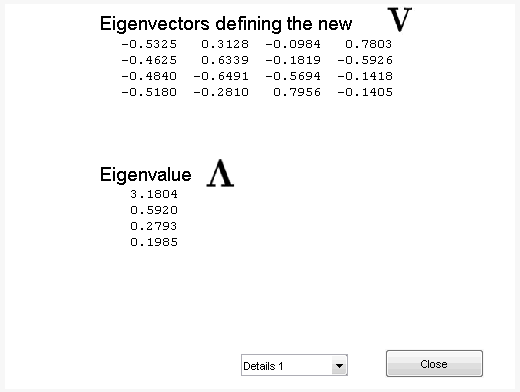
Можно изменить уровень или выбрать более грубые приближения или восстановленную матрицу, чтобы исследовать различные основы. Когда вы закончите, нажмите Close.
Выполните простой многошкальный PCA.
Начальные значения для PCA приводят к сохранению всех компонентов. Выберите Kaiser из Обеспечить значения по умолчанию с помощью выпадающего списка и нажмите Apply.
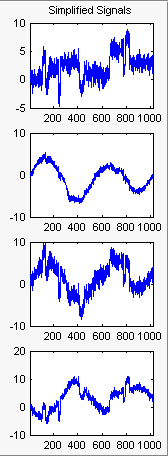
Результаты хороши с точки зрения сжатия.
Улучшите полученный результат путем сохранения меньшего количества основных компонентов.
Результаты могут быть улучшены путем подавления шума, потому что детали на уровнях 1 - 3 составлены по существу шума с маленькими вкладами от сигнала, как вы видите тщательным контролем коэффициентов детали. Удаление шума приводит к сырой нефти, но большой, эффект шумоподавления.
Для D1, D2 и D3, выбирают 0 как Nb. PC нев центре и нажимают Apply.
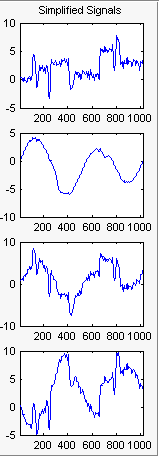
Результаты лучше, чем ранее полученные. Первый сигнал, который неправилен, все еще правильно восстанавливается, в то время как второй сигнал, который является более регулярным, является denoised лучше после этого второго этапа PCA. Можно получить больше информации путем нажатия на Residuals.
Инструмент Multiscale Principal Components Analysis позволяет вам сохранить упрощенные сигналы на диск. Тулбокс создает MAT-файл в текущей папке с именем по вашему выбору.
Избавить упрощенные сигналы от предыдущего раздела:
Выберите File> Save Simplified Signals.
Выберите Save Simplified Signals и Parameters. Диалоговое окно появляется, который позволяет вам задать папку и имя файла для хранения сигнала.
Введите имя s_ex4mwden и нажмите ОК, чтобы сохранить данные.
Загрузите переменные в свою рабочую область:
load s_ex4mwden whos
| Имя | Размер | Байты | Класс |
|---|---|---|---|
PCA_Params | 1x7 | 2628 | struct array |
x | 1024x4 | 32768 | double array |
Упрощенные сигналы находятся в матричном x. Параметры многошкального PCA доступны в PCA_Params:
PCA_Params
PCA_Params =
1x7 struct array with fields:
pc
variances
npc
PCA_Params является массивом структур длины d+2 (здесь, максимальный уровень разложения d=5) таким образом, что PCA_Params(d).pc является матрицей основных компонентов. Столбцы хранятся в порядке убывания отклонений. PCA_Params(d).variances является вектором отклонений основного компонента, и PCA_Params(d).npc является вектором выбранных количеств сохраненных основных компонентов.