Системы координат позволяют вам отслеживать самолет или положение космического корабля и ориентацию на пробеле. Системы координат Aerospace Blockset™ основаны на этих базовых концепциях от геодезии, астрономии и физики.
blockset использует предназначенные для правой руки (RH) системы Декартовой координаты. Правило правой руки устанавливает x-y-z последовательность осей координат.
Инерционная система координат является не ускоряющейся системой координат движения. В инерционной системе координат второй закон Ньютона содержит: обеспечьте = масса × ускорение. Свободно разговор, ускорение задано относительно удаленного космоса, и инерционная система координат, как часто говорят, не ускоряется относительно “фиксированных звезд”. Поскольку Земля и перемещение звезд так медленно друг относительно друга, это предположение является очень точным приближением.
Строго заданный, инерционная система координат является членом набора всех систем координат, не ускоряющихся друг относительно друга. Неинерционная система координат является любой системой координат, ускоряющейся относительно инерционной системы координат. Его ускорение, в целом, включает и поступательные и вращательные компоненты, приводящие к псевдосилам (псевдосила тяжести, а также Кориолис и центробежные силы).
blockset модели форма Земли (геоид) как сжатый сфероид, специальный тип эллипсоида с двумя более длинными равными осями (определение экваториальной плоскости) и одна треть, немного короче (геополярная) ось симметрии. Экватор является пересечением экваториальной плоскости и поверхности Земли. Географические полюса являются пересечением поверхности Земли и геополярной оси. В общем случае геополярная Земля и оси вращения не идентична.
Широты параллельны экватору. Долготы параллельны геополярной оси. Нулевая долгота или главный меридиан проходят через Гринвич, Англия.
blockset делает три стандартных приближения в определении систем координат относительно Земли.
Поверхность или геоид Земли являются сжатым сфероидом, заданным его более длинными экваториальными и более короткими геополярными осями. В действительности Земля немного деформирована относительно стандартного геоида.
Ось вращения Земли и экваториальная плоскость перпендикулярны, так, чтобы вращение и геополярные оси были идентичны. В действительности эти оси немного неправильно выравниваются, и экваториальные плоские колебания, когда Земля вращается. Этот эффект незначителен в большинстве приложений.
Единственный неинерционный эффект в зафиксированных Землей координатах происходит из-за вращения Земли вокруг его оси. Это - вращение, геоцентрическая система. blockset игнорирует ускорение Земли вокруг Sun, ускорение Sun в Галактике и ускорение Галактики через космос. В большинстве приложений, только вопросы вращения Земли.
Это приближение должно быть изменено для космического корабля, отправленного в глубокий космос, т.е. вне Лунной Землей системы, и предпочтена гелиоцентрическая система.
blockset использует стандартный геоид WGS-84, чтобы смоделировать Землю. Можно изменить экваториальную длину оси, выравнивание и уровень вращения.
Можно представлять движение космического корабля относительно любого небесного тела, которое хорошо аппроксимировано сжатым сфероидом путем изменения сфероидального размера, выравнивания и уровня вращения. Если небесное тело вращается движущийся на запад (retrogradely), сделайте уровень вращения отрицательным.
Моделирование самолета и космического корабля является самым простым, если вы используете систему координат, зафиксированную в самом теле. В случае самолета прямое направление изменяется присутствием ветра, и движение ремесла через воздух не является тем же самым как своим движением относительно земли.
Смотрите уравнения Движения для получения дальнейшей информации о том, как продукт Aerospace Blockset реализует координаты ветра и тело.
Неинерционная система координат тела фиксируется и в источнике и в ориентации к движущемуся ремеслу. Ремесло принято, чтобы быть твердым.
Ориентация осей координат тела фиксируется в форме тела.
Ось X указывает через нос ремесла.
Ось Y указывает справа от оси X (стоящий в направлении пилота представления), перпендикуляр к оси X.
Ось z указывает вниз через нижнюю часть ремесло, перпендикуляр к xy плоскости и удовлетворению правилу RH.
Поступательные Степени свободы. Переводы заданы путем прохождения этих осей расстояниями x, y, и z от источника.
Вращательные Степени свободы. Вращения заданы Углами Эйлера P, Q, R или Φ, Θ, Ψ. Они:
| P или Φ | Перекатывайтесь ось X |
| Q или Θ | Сделайте подачу об оси Y |
| R или Ψ | Отклоняйтесь от курса об оси z |
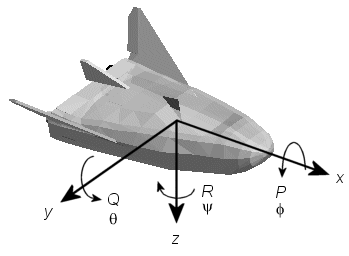
Если в противном случае не задано, по умолчанию программное обеспечение использует порядок вращения ZYX для Углов Эйлера.
Неинерционная система координат ветра возникает зафиксированная в твердом самолете. Ориентация системы координат задана относительно скорости ремесла V.
Ориентация осей координат ветра фиксируется скоростью V.
Ось X указывает в направлении V.
Ось Y указывает справа от оси X (стоящий в направлении V), перпендикуляр к оси X.
Ось z указывает, что перпендикуляр к xy плоскости любым способом должен был удовлетворить правилу RH относительно x-и yaxes.
Поступательные Степени свободы. Переводы заданы путем прохождения этих осей расстояниями x, y, и z от источника.
Вращательные Степени свободы. Вращения заданы Углами Эйлера Φ, γ, χ. Они:
| Φ | Угол банка об оси X |
| γ | Курс полета об оси Y |
| χ | Заголовок угла об оси z |
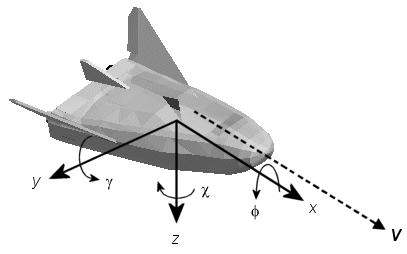
Если в противном случае не задано, по умолчанию программное обеспечение использует порядок вращения ZYX для Углов Эйлера.
Моделирование космических траекторий требует расположения и ориентации самолета или космического корабля относительно вращающейся Земли. Координаты навигации заданы относительно центра и поверхности Земли.
Геоцентрическая широта λ на поверхности Земли задана углом, за которым подухаживает радиус-вектор от центра Земли до поверхностной точки с экваториальной плоскостью.
Геодезическая широта µ на поверхности Земли задана углом, за которым подухаживает поверхностный вектор нормали n и экваториальная плоскость.
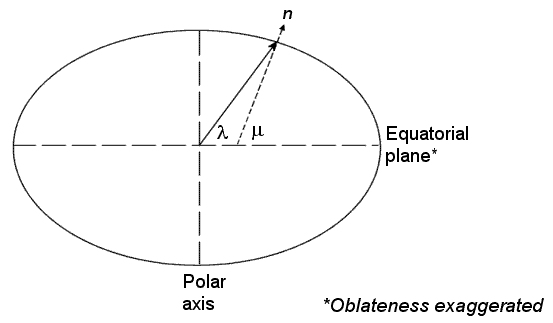
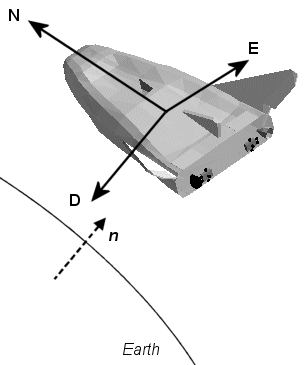
Северо-восток вниз (NED) система является неинерционной системой со своим источником, зафиксированным в самолете или центре тяжести космического корабля. Его оси ориентированы вдоль геодезических направлений, заданных поверхностью Земли.
Ось X указывает северную параллель на поверхность геоида в полярном направлении.
Ось Y указывает восточную параллель на поверхность геоида вдоль кривой широты.
Ось z указывает вниз, к поверхности Земли, антипараллельной к исходящему нормальному n поверхности.
Полет на постоянной высоте означает лететь в постоянном z выше поверхности Земли.
Система Сосредоточенного землей инерционного (ECI) не вращается. Для большинства приложений примите эту систему координат, чтобы быть инерционными, несмотря на то, что равноденствие и экваториальное плоское перемещение очень немного в зависимости от времени. Система ECI считается действительно инерционной для вычислений орбиты высокой точности, когда экватор и равноденствие заданы в конкретную эпоху (например, J2000). Космические функции и блоки, которые используют конкретную реализацию системы координат ECI, предоставляют ту информацию в своей документации. Системный источник ECI фиксируется в центре Земли (см. рис.).
Ось X указывает на весеннее равноденствие (Первая Точка Овна ♈).
Ось Y указывает 90 градусов на восток оси X в экваториальной плоскости.
Ось z указывает к северу вдоль Наземной оси вращения.
Сосредоточенные землей координаты
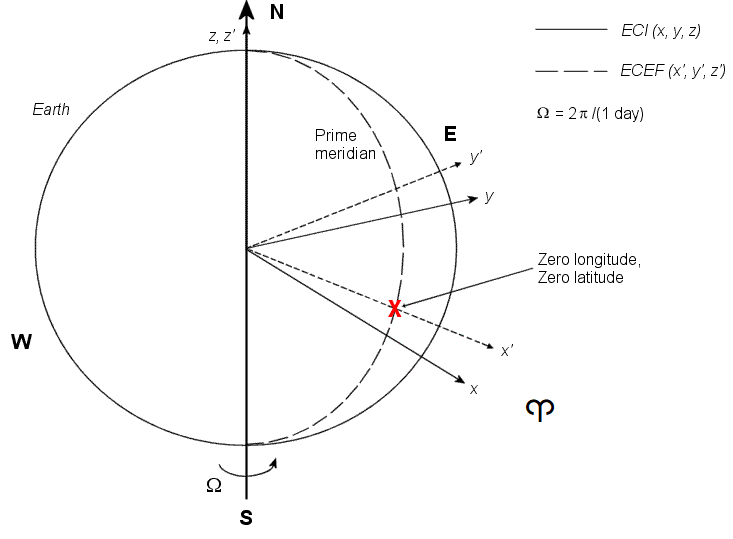
Наземный центр, зафиксированная Землей система (ECEF) является неинерционной и вращается с Землей. Его источник фиксируется в центре Земли (см. предыдущую фигуру).
X -ось указывает на пересечение экваториальной плоскости Земли и Гринвичский меридиан.
Y -ось указывает 90 градусов на восток x '-оси в экваториальной плоскости.
Z -ось указывает к северу вдоль оси вращения Земли.
Несколько инструментов отображения доступны для использования с продуктом Aerospace Blockset. У каждого есть определенная система координат для рендеринга движения.
См. Внешний вид осей (MATLAB) для получения дополнительной информации об осях координат MATLAB® Graphics.
Графика MATLAB использует эту ориентацию координатной оси по умолчанию:
Ось X указывает из экрана.
Ось Y указывает направо.
Ось z подчеркивает.
FlightGear является открытым исходным кодом, сторонним средством моделирования рейса с интерфейсом, поддержанным blockset.
Работа с Интерфейсом Средства моделирования Рейса обсуждает интерфейс blockset к FlightGear.
См. документацию FlightGear в www.flightgear.org для полной информации об этом средстве моделирования рейса.
Координаты FlightGear формируют специальную зафиксированную телом систему, вращаемую от стандартной системы координат тела об оси Y-180 градусами:
Ось X положительна к задней части транспортного средства.
Ось Y положительна к праву на транспортное средство.
Ось z положительна восходящий, например, колеса обычно имеют самые низкие z значения.
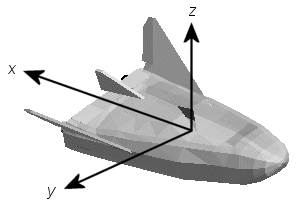
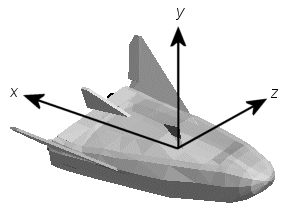
AC3D является недорогим, широко используемым, редактор геометрии, доступный от www.ac3d.org. Его системы координат, связанные с телом формируются путем инвертирования трех стандартных осей координат тела:
Ось X положительна к задней части транспортного средства.
Ось Y положительна восходящий, например, колеса обычно имеют самые низкие y значения.
Ось z положительна слева от транспортного средства.
Методические рекомендации для атмосферного и систем координат транспортного средства космического полета, R-004-1992, ANSI/AIAA, февраль 1992.
Документация Mapping Toolbox, MathWorks, Inc., Натик, Массачусетс. Mapping Toolbox.
Роджерс, R. M. прикладная математика в интегрированных системах навигации, AIAA, Рестоне, Вирджиния, 2000.
Sobel, D., Longitude, Walker & Company, Нью-Йорк, 1995.
Стивенс, B. L., и Ф. Л. Льюис, Управление Самолетом и Симуляция, 2-й редактор, Управление Самолетом и Симуляция, Wiley-межнаука, Нью-Йорк, 2003.
Томсон, W. T. Введение в Space Dynamics, John Wiley & Sons, Нью-Йорк, 1961/Дувр Публикация, Майнеола, Нью-Йорк, 1986.
Мировая геодезическая система 1984 (WGS 84), http://earth-info.nga.mil/GandG/wgs84/.