Сгенерируйте биты CRC кода и добавьте к входным данным
comm.CRCGenerator Система object™ генерирует биты контроля циклическим избыточным кодом (CRC) кода для каждого входного кадра и добавляет их к системе координат. Для получения дополнительной информации смотрите Работу Генератора CRC.
Сгенерировать биты CRC кода для каждого входного кадра и добавить их к системе координат:
Создайте comm.CRCGenerator объект и набор его свойства.
Вызовите объект с аргументами, как будто это была функция.
Чтобы узнать больше, как Системные объекты работают, смотрите то, Что Системные объекты? MATLAB.
crcgenerator= comm.CRCGenerator
crcgenerator = comm.CRCGenerator(Name,Value)comm.CRCGenerator('Polynomial','z^16 + z^14 + z + 1') конфигурирует Системный объект генератора CRC, чтобы добавить биты CRC-16 контроля циклическим избыточным кодом к входному кадру. Заключите каждое имя свойства в кавычки.
crcgenerator = comm.CRCGenerator(poly,Name,Value)Polynomial набор свойств к poly, и другой заданный набор свойств к заданным значениям.
Если в противном случае не обозначено, свойства являются ненастраиваемыми, что означает, что вы не можете изменить их значения после вызова объекта. Объекты блокируют, когда вы вызываете их и release функция разблокировала их.
Если свойство является настраиваемым, можно изменить его значение в любое время.
Для получения дополнительной информации об изменении значений свойств смотрите Разработку системы в MATLAB Используя Системные объекты (MATLAB).
Polynomial — Полином генератора'z^16 + z^12 + z^5 + 1' (значение по умолчанию) | полиномиальный вектор символов | вектор строки двоичных знаков | целочисленный вектор-строкаПолином генератора для алгоритма CRC, заданного как одно из следующего:
Полиномиальный вектор символов, такой как 'z^3 + z^2 + 1'.
Вектор строки двоичных знаков, который представляет коэффициенты полинома генератора в порядке убывающей степени. Длина этого вектора (N +1), где N является степенью полинома генератора. Например, [1 1 0 1] представляет полиномиальный x 3 + z 2 + 1.
Целочисленный вектор-строка, содержащий экспоненты z для ненулевых условий в полиноме в порядке убывания. Например, [3 2 0] представляет полиномиальный z 3 + z 2 + 1.
Для получения дополнительной информации смотрите Символьное представление Полиномов.
Некоторые обычно используемые полиномы генератора включают:
| Метод CRC | Полином генератора |
|---|---|
| CRC-32 | 'z^32 + z^26 + z^23 + z^22 + z^16 + z^12 + z^11 + z^10 + z^8 + z^7 + z^5 + z^4 + z^2 + z + 1' |
| CRC-24 | 'z^24 + z^23 + z^14 + z^12 + z^8 + 1' |
| CRC-16 | 'z^16 + z^15 + z^2 + 1' |
| Обратный CRC-16 | 'z^16 + z^14 + z + 1' |
| CRC-8 | 'z^8 + z^7 + z^6 + z^4 + z^2 + 1' |
| CRC-4 | 'z^4 + z^3 + z^2 + z + 1' |
Пример: 'z^7 + z^2 + 1', [1 0 0 0 0 1 0 1], и [7 2 0] представляйте тот же полином, p (z) = z
7 + z
2 + 1.
Типы данных: double | char
InitialConditions — Начальные состояния внутреннего сдвигового регистра1 | вектор строки двоичных знаковНачальные состояния внутреннего сдвигового регистра, заданного как бинарный скаляр или вектор строки двоичных знаков с длиной, равняются степени полинома генератора. Скалярное значение расширено до вектора-строки из равной длины до степени полинома генератора.
Типы данных: логический
DirectMethod — Используйте прямой алгоритм в вычислениях контрольной суммы CRCfalse (значение по умолчанию) | trueИспользуйте прямой алгоритм в вычислениях контрольной суммы CRC, заданных как false или true.
Когда вы устанавливаете это свойство на true, объект использует прямой алгоритм в вычислениях контрольной суммы CRC. Когда вы устанавливаете это свойство на false, объект использует непрямой алгоритм в вычислениях контрольной суммы CRC.
Для получения дополнительной информации о прямых и непрямых алгоритмах смотрите Выявление ошибок и Коррекцию.
Типы данных: логический
ReflectInputBytes — Отразите входные байтыfalse (значение по умолчанию) | trueОтразите входные байты, заданные как false или true. Установите это свойство на true инвертировать входной кадр на bytewise основе прежде, чем ввести данные в сдвиговый регистр.
Когда вы устанавливаете это свойство на true, длина входного кадра, разделенная на значение ChecksumsPerFrame свойство должно быть целым числом и кратным 8.
Типы данных: логический
ReflectChecksums — Отразите контрольные суммы перед итоговым XORfalse (значение по умолчанию) | trueОтразите контрольные суммы перед итоговым XOR, заданным как false или true. Установите это свойство на true чтобы инвертировать контрольные суммы CRC вокруг их центров после, входные данные полностью через сдвиговый регистр.
Типы данных: логический
FinalXOR — Итоговый XORИтоговые XOR, заданные как бинарный скаляр или вектор строки двоичных знаков с длиной, равняются степени полинома генератора. Запуски операции "исключающее ИЛИ" с помощью значения FinalXOR свойство и контрольная сумма CRC прежде, чем соответствовать входной контрольной сумме. Скалярное значение расширено до вектора-строки из равной длины до степени полинома генератора. Установка 0 не эквивалентно никакой операции "исключающее ИЛИ".
Типы данных: логический
ChecksumsPerFrame — Количество контрольных сумм вычисляется для каждой системы координатКоличество контрольных сумм вычисляется для каждой системы координат, заданной как положительное целое число. Для получения дополнительной информации смотрите Работу Генератора CRC.
Типы данных: double
x — Входной сигналВходной сигнал, заданный как вектор столбца двоичных данных. Длина входного кадра должна быть кратной значению ChecksumsPerFrame свойство. Если тип входных данных является двойным, младший значащий бит используется в качестве двоичного значения. Для получения дополнительной информации смотрите Работу Генератора CRC.
Типы данных: double | logical
codeword — Выведите систему координат кодовой комбинацииВыведите систему координат кодовой комбинации, возвращенную как вектор столбца двоичных данных, который наследовал тип данных входного сигнала. Выход содержит входные кадры с добавленными битами кодовой последовательности CRC.
Длиной выходной системы координат кодовой комбинации является m + k * r, где m является размером входного сигнала, k является количеством контрольных сумм на входной кадр, и r является степенью полинома генератора. Для получения дополнительной информации смотрите Работу Генератора CRC.
Чтобы использовать объектную функцию, задайте Системный объект как первый входной параметр. Например, чтобы выпустить системные ресурсы Системного объекта под названием obj, используйте этот синтаксис:
release(obj)
Сгенерируйте контрольную сумму CRC-8 для примера, показанного в 802.11™-2016 [1], разделите 21.3.10.3 и сравните с ожидаемым CRC.
Создайте Систему Генератора CRC object™. Чтобы выровняться с вычислением CRC в 802.11-20016, Система object™ устанавливает полином генератора как , начальные состояния к 1, прямой метод и итоговый XOR к 1.
crc8 = comm.CRCGenerator('Polynomial','z^8 + z^2 + z + 1', ... 'InitialConditions',1,'DirectMethod',true,'FinalXOR',1)
crc8 =
comm.CRCGenerator with properties:
Polynomial: 'z^8 + z^2 + z + 1'
InitialConditions: 1
DirectMethod: true
ReflectInputBytes: false
ReflectChecksums: false
FinalXOR: 1
ChecksumsPerFrame: 1
Обработайте один входной кадр согласно примеру из 802.11-2016 стандартов в разделе 21.3.10.3. В примере, входной поток битов {m0, … m22} {1 0 0 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1} и ожидаемая контрольная сумма CRC {c7, … c0} {0 0 0 1 1 1 0 0}.
x = [1 0 0 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1]'; expectedChecksum = [0 0 0 1 1 1 0 0]'; checksumLength = length(expectedChecksum);
Сгенерированная контрольная сумма CRC сравнивается с ожидаемой контрольной суммой.
codeword = crc8(x); checksum = codeword(end-checksumLength+1:end); isequal(checksum,expectedChecksum)
ans = logical
1
Ссылки
[1] Станд. IEEE 802.11™-2016 стандарт IEEE для информационных технологий — локальных сетей и городских компьютерных сетей — часть 11 конкретных требований: беспроводная связь ЛЭН МАК и спецификации PHY.
Передайте двоичные данные через генератор CRC, введите немного ошибки и обнаружьте ошибку детектор CRC.
Создайте случайный бинарный вектор.
x = randi([0 1],12,1);
Закодируйте систему координат входного сигнала с помощью генератора CRC с ChecksumsPerFrame набор свойств к 2. Это подразделяет входящую систему координат на два подкадра равной длины.
crcgenerator = comm.CRCGenerator([1 0 0 1],'ChecksumsPerFrame',2);
codeword = crcgenerator(x);Декодируйте кодовую комбинацию и проверьте, что нет никаких ошибок ни в одном подкадре.
crcdetector = comm.CRCDetector([1 0 0 1],'ChecksumsPerFrame',2);
[~, err] = crcdetector(codeword)err = 2×1
0
0
Введите ошибку во втором подкадре путем инвертирования последнего элемента подкадра 2. Передайте поврежденную кодовую комбинацию через детектор CRC и проверьте, что ошибка обнаруживается во втором подкадре.
codeword(end) = not(codeword(end)); [~,err] = crcdetector(codeword)
err = 2×1
0
1
Используйте код CRC, чтобы обнаружить ошибки системы координат в шумном сигнале BPSK.
Создайте пару генератора и детектора CRC использование стандартного полинома CRC-4, .
poly = 'z4+z3+z2+z+1';
crcgenerator = comm.CRCGenerator(poly);
crcdetector = comm.CRCDetector(poly);Сгенерируйте 12-битные системы координат двоичных данных и добавьте биты CRC. На основе степени полинома 4 бита добавлены к каждой системе координат. Примените модуляцию BPSK и передайте сигнал через канал AWGN. Демодулируйте и используйте детектор CRC, чтобы определить, по ошибке ли система координат.
numFrames = 20; frmError = zeros(numFrames,1); for k = 1:numFrames data = randi([0 1],12,1); % Generate binary data encData = crcgenerator(data); % Append CRC bits modData = pskmod(encData,2); % BPSK modulate rxSig = awgn(modData,5); % AWGN channel, SNR = 5 dB demodData = pskdemod(rxSig,2); % BPSK demodulate [~,frmError(k)] = crcdetector(demodData); % Detect CRC errors end
Идентифицируйте системы координат, в которых обнаруживаются битовые ошибки CRC кода.
find(frmError)
ans = 6
Создайте CRC-16-CCITT генератор как описано в Разделе 2.2.7.4 из Рекомендации X-25 [1] ITU-T с помощью входных данных и ожидаемой последовательности проверки системы координат (FCS) из Примера 2 в Приложении I, I.1.
Создайте систему координат ответа непронумерованного подтверждения (UA) где адрес = B и F = 1.
Address = [1 0 0 0 0 0 0 0]; UA = [1 1 0 0 1 1 1 0]; input = [Address UA]'; expectedChecksum = [1 1 0 0 0 0 0 1 1 1 1 0 1 0 1 0]'; % Expected FCS checksumLength = 16; crcGen = comm.CRCGenerator(... 'Polynomial','X^16 + X^12 + X^5 + 1',... 'InitialConditions',1,... 'DirectMethod',true,... 'FinalXOR',1); crcSeq = crcGen(input); checkSum = crcSeq(end-checksumLength+1:end);
Сравните вычисленную контрольную сумму с ожидаемой контрольной суммой.
isequal(expectedChecksum,checkSum)
ans = logical
1
Ссылки
[1] ITU Сектор стандартизации электросвязи. Серия X: Сети передачи данных И Коммуникация Открытой системы. Общедоступные сети передачи данных – Интерфейсы. 1997
Создайте код CRC-32 для поля последовательности проверки системы координат (FCS) для Ethernet как описано в Разделе 3.2.9 из Стандарта IEEE для Ethernet[1].
rng(1865); % Seed the random number generator for repeatable resultsИнициализируйте сообщение со случайными данными, чтобы представлять защищенные поля системы координат MAC, в частности адрес назначения, исходный адрес, длина или поле типа, клиентские данные MAC и дополнение.
data = randi([0,1],100,1);
Задайте генерирующийся полином CRC-32, используемый в кодировании сообщений Ethernet.
poly = [32,26,23,22,16,12,11,10,8,7,5,4,2,1,0];
Вычислите CRC путем выполнения шагов, заданных в стандарте и использования непрямого метода, чтобы сгенерировать код CRC.
dataN = [not(data(1:32));data(33:end)]; % Section 3.2.9 step a) and b) crcGen1 = comm.CRCGenerator(... 'Polynomial', poly, ... 'InitialConditions', 0, ... 'DirectMethod', false, ... 'FinalXOR', 1); seq = crcGen1(dataN); % Section 3.2.9 step c), d) and e) csNondirect = seq(end-31:end);
Вычислите CRC путем выполнения шагов, заданных в стандарте и использования прямого метода сгенерировать код CRC.
crcGen2 = comm.CRCGenerator(... 'Polynomial', poly, ... 'InitialConditions', 1, ... 'DirectMethod', true, ... 'FinalXOR', 1); txSeq = crcGen2(data); csDirect = txSeq(end-31:end);
Сравните сгенерированные коды CRC при помощи непрямых и прямых методов.
disp([csNondirect';csDirect']);
Columns 1 through 13
1 1 1 0 1 1 0 0 1 0 0 1 0
1 1 1 0 1 1 0 0 1 0 0 1 0
Columns 14 through 26
1 0 0 1 0 1 0 1 1 0 0 0 1
1 0 0 1 0 1 0 1 1 0 0 0 1
Columns 27 through 32
1 1 0 0 1 0
1 1 0 0 1 0
isequal(csNondirect,csDirect)
ans = logical
1
rng('default'); % Reset the random number generator
Ссылки
[1] Общество эпохи компьютеризации IEEE. Стандарт IEEE для Ethernet: станд. 802.3-2012. Нью-Йорк, Нью-Йорк: 2012.
Кодирование контроля циклическим избыточным кодом (CRC) является методом кодирования контроля ошибок для обнаружения ошибок, которые происходят, когда кадр данных передается. В отличие от блочных или сверточных кодов, коды CRC не имеют встроенной возможности исправления ошибок. Вместо этого когда система связи обнаруживает ошибку в полученной кодовой комбинации, получатель запрашивает отправителя ретранслировать кодовую комбинацию.
В кодировании CRC передатчик применяет правило к каждой системе координат данных, чтобы создать дополнительные биты CRC, названные контрольной суммой или синдромом, и затем добавляет контрольную сумму к системе координат данных. После получения переданной кодовой комбинации получатель применяет то же правило к полученной кодовой комбинации. Если получившаяся контрольная сумма является ненулевой, ошибка произошла, и передатчик должен снова послать систему координат данных.
Когда количество контрольных сумм на систему координат больше 1, система координат входных данных разделена на подкадры, правило применяется к каждому подкадру данных, и отдельные контрольные суммы добавлены к каждому подкадру. Кодовые комбинации подкадра конкатенированы, чтобы вывести одну систему координат.
Для обсуждения поддерживаемых алгоритмов CRC см. Коды Контроля циклическим избыточным кодом.
Генератор CRC добавляет контрольные суммы CRC к входному кадру согласно заданному полиному генератора и количеству контрольных сумм на систему координат.
Для определенного начального состояния внутреннего сдвигового регистра и контрольных сумм k на входной кадр:
Входной сигнал разделен на подкадры k равного размера.
Каждый из подкадров k снабжается префиксом вектор начальных состояний.
Алгоритм CRC применяется к каждому подкадру.
Получившиеся контрольные суммы добавлены в конец каждого подкадра.
Подкадры конкатенированы и выведены как вектор-столбец.
Для сценария, показанного здесь, вводится 10-битная система координат, третий полином генератора степени вычисляет контрольную сумму CRC, начальное состояние 0, и количество контрольных сумм на систему координат равняется 2.
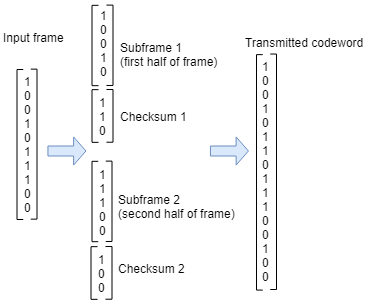
Входной кадр разделен на два подкадра размера 5, и контрольные суммы размера 3 вычислены и добавлены к каждому подкадру. Начальные состояния не показывают, потому что начальное состояние [0] не влияет на выход алгоритма CRC. Переданный кадр кодовой комбинации выхода имеет размер 5 + 3 + 5 + 3 = 16.
[1] Sklar, Бернард. Цифровая связь: основные принципы и приложения. Englewood Cliffs, Нью-Джерси: Prentice Hall, 1988.
[2] Ивовый прут, системы контроля ошибок Стивена Б. для цифровой связи и устройства хранения данных. Верхний Сэддл-Ривер, Нью-Джерси: Prentice Hall, 1995.
Указания и ограничения по применению:
Смотрите системные объекты в Генерации кода MATLAB (MATLAB Coder).
У вас есть модифицированная версия этого примера. Вы хотите открыть этот пример со своими редактированиями?
1. Если смысл перевода понятен, то лучше оставьте как есть и не придирайтесь к словам, синонимам и тому подобному. О вкусах не спорим.
2. Не дополняйте перевод комментариями “от себя”. В исправлении не должно появляться дополнительных смыслов и комментариев, отсутствующих в оригинале. Такие правки не получится интегрировать в алгоритме автоматического перевода.
3. Сохраняйте структуру оригинального текста - например, не разбивайте одно предложение на два.
4. Не имеет смысла однотипное исправление перевода какого-то термина во всех предложениях. Исправляйте только в одном месте. Когда Вашу правку одобрят, это исправление будет алгоритмически распространено и на другие части документации.
5. По иным вопросам, например если надо исправить заблокированное для перевода слово, обратитесь к редакторам через форму технической поддержки.