Декодер турбо кода продукта (TPC)
decoded = tpcdec(llr,N,K,S,maxnumiter,earlyterm)maxnumiter декодирование итераций. Использовать maxnumiter и earlyterm с сообщениями во всю длину задайте S как пустой, [].
[также возвращает фактическое количество декодирования итераций после выполнения 2D TPC, декодирующего использующий любой из предшествующих синтаксисов.decoded,actualnumiter] = tpcdec(___)
Турбо коды продуктов (TPC) являются формой каскадных кодов, используемых в качестве кодов прямого исправления ошибок (FEC). Два или больше блочных кода компонента, такие как систематические линейные блочные коды, используются, чтобы создать TPCs. Декодер TPC достигает почти оптимального декодирования кодов продуктов с помощью Чейза, декодирующего и алгоритма Pyndiah, чтобы выполнить итеративный мягкий вход, мягкое выходное декодирование. Для подробного описания см. [1] и [2]. Этот декодер реализует итеративный мягкий вход, мягкий выход 2D декодирование кода продукта, как описано в [2], с помощью двух Линейных Блочных кодов. Декодер ожидает мягкие битные логарифмические отношения правдоподобия (LLRs), полученный из цифровой демодуляции как входной сигнал.
Декодер TPC ожидает положительный биполярный сопоставленный вход, в частности –1 сопоставленный к 0 и +1 сопоставленный к 1. Выход от демодуляторов в Communications Toolbox™ является отрицательным биполярным отображением, в частности +1 сопоставленный к 0 и –1 сопоставленный к +1. Поэтому LLR выход от демодуляторов должен отрицаться, чтобы обеспечить положительный биполярный сопоставленный вход, ожидаемый декодером TPC.
TPC декодирование сообщений во всю длину
Закодированные входные сигналы TPC во всю длину декодируются с помощью, задал 2D пары кода TPC. Построчное декодирование использует (N C, K C) пара кода и по столбцам декодирование использования (N R, K R) пара кода. Длиной входного вектора должен быть N R × N C. Чтобы выполнить 2D декодирование TPC, вектор-столбец входа LLRs, состоявшего из сообщения и битов четности, располагается в матрицу R-by-NC N.
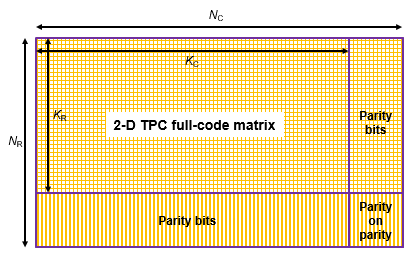
Декодер TPC достигает почти оптимального декодирования кодов продуктов с помощью Чейза, декодирующего и алгоритма Pyndiah, чтобы выполнить итеративный мягкий вход, мягкое выходное декодирование. Чейз, декодирующий, формирует набор возможных кодовых комбинаций для каждой строки или столбца. Алгоритм Pyndiah вычисляет мягкую информацию, запрошенную для следующего шага декодирования.
Итеративный мягкий вход, мягкий Выходной декодер
Итеративный мягкий вход, мягкое выходное декодирование, как показано в блок-схеме, выполняет два шага декодирования для каждой итерации.
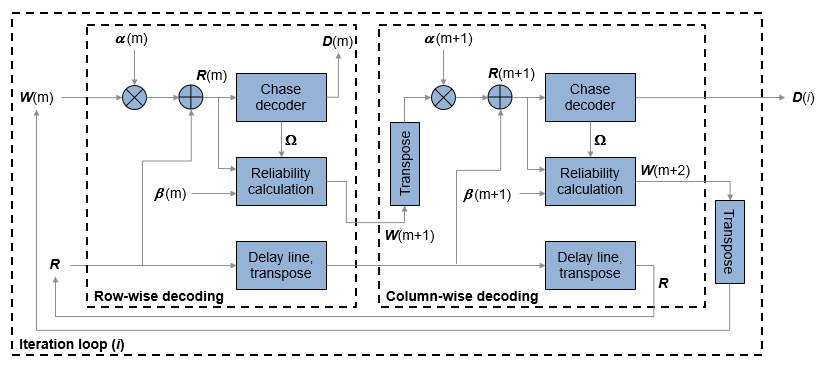
Мягкими входными параметрами для декодирования является R (m) = R + α (m) W (m).
Счетчик цикла итерации i постепенно увеличивается от i = 1 к конкретному количеству итераций.
m = 2i 1 индекс шага декодирования.
R является полученной матрицей LLR.
R (m) является мягким входом для m th декодирующий шаг.
W (m) является входной информацией о значении внешних параметров для m th декодирующий шаг.
α (m) = [0,0.2,0.3,0.5,0.7,0.9,1,1...], где α является фактором взвешивания, примененным на основе индекса шага декодирования. Для более высоких шагов декодирования, α = 1.
β (m) = [0.2,0.4,0.6,0.8,1,1...], где β является фактором надежности, примененным на основе индекса шага декодирования. Для более высоких шагов декодирования, β = 1.
D содержит декодируемые биты сообщения. Биты выходного сигнала формируются из D путем отображения –1 к 0 и +1 к 1, затем изменения блока сообщения в вектор-столбец.
Биты выходного сигнала формируются после итерации через конкретное количество итераций, или, если раннее завершение включено после сходимости кода.
Раннее завершение декодирования TPC
Если раннее завершение включено, проверка сходимости кода выполнена на трудном решении о мягком входе на каждом построчном и постолбцовом шаге декодирования. Раннее завершение может быть инициировано, или после сходятся построчное декодирование или после постолбцовое декодирование.
Код сходится если для всех строк или всех столбцов,
Синдром оценивает, чтобы обнулить в кодах (Коды Хемминга, Расширенные Коды Хемминга, коды BCH или Расширенные коды BCH).
Проверка четности оценена, чтобы обнулить в кодах с проверкой четности.
Количество, о котором сообщают, итераций оценивает к значению итерации, которое в настоящее время происходит. Например, если проверке сходимости кода удовлетворяют после построчного декодирования в третьей итерации (после того, как 2,5 декодирования продвигаются), затем количество возвращенной итерации равняется 3.
TPC декодирование сокращенных сообщений
Закодированные сокращенные входные сигналы TPC декодируются с помощью, задал 2D пары кода TPC. Построчное декодирование использует (N C – K C + S C, S C) пара кода и по столбцам декодирование использования (N R – K R + S R, S R) пара кода. Длина входного вектора должна быть (N R – K R + S R) × (N C– K C + S C). Чтобы выполнить 2D декодирование TPC сокращенных сообщений, вектор-столбец входа LLRs, состоявшего из сокращенного сообщения и битов четности, располагается в (N R – K R + S R) (N C – K C + S C) матрица.
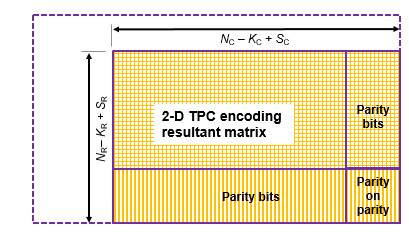
Декодер TPC обрабатывает полученное сокращенное сообщение LLRs, похожий на полные коды за этими исключениями:
Сокращенные позиции двоичного разряда в полученной кодовой комбинации установлены в –1.
Алгоритм Преследования не рассматривает сокращенных позиций двоичного разряда при выборе наименее надежных битов.
[1] Преследуйте, D. "Класс Алгоритмов для Декодирования Блочных кодов с информацией об Измерении Канала". Транзакции IEEE на Теории информации, Объем 18, Номер 1, январь 1972, стр 170–182.
[2] Pyndiah, R. M. "Почти оптимальное Декодирование Кодов продуктов: Блокируйте Турбокоды". Транзакции IEEE на Коммуникациях. Объем 46, Номер 8, август 1998, стр 1003–1010.