Симулируйте ответ времени динамической системы к произвольным входным параметрам
lsim(sys,u,t)
lsim(sys,u,t,x0)
lsim(sys,u,t,x0,method)
lsim(sys1,...,sysn,u,t)
lsim(sys1,LineSpec1,...,sysN,LineSpecN,u,t)
y = lsim(___)
[y,t,x] = lsim(___)
lsim(sys)
lsim симулирует (время) ответ непрерывных или дискретных линейных систем к произвольным входным параметрам. Когда вызвано без левых аргументов, lsim строит ответ на экране.
lsim(sys,u,t) производит график ответа времени модели sys динамической системы к входной истории, tU. Векторный t задает выборки времени для симуляции (в модулях системного времени, заданных в TimeUnit свойство sys), и состоит из расположенных с равными интервалами выборок времени:
t = 0:dt:Tfinal
Вход u массив, имеющий столько же строк сколько выборки времени (length(t)) и столько же столбцов сколько системные входные параметры. Например, если sys система SISO, затем u t-1 вектор. Если sys имеет три входных параметров, затем u t-3 массив. Каждая строка u(i,:) задает входное значение (значения) в то время демонстрационный t(i). u сигнала также появляется на графике.
Модель sys может быть непрерывным или дискретным, SISO или MIMO. В дискретное время, u должен быть произведен на том же уровне как система. В этом случае, вход t избыточно и может быть не использован или установлен в пустую матрицу. В непрерывное время, временная выборка dt = t(2)-t(1) используется, чтобы дискретизировать непрерывную модель. Если dt является слишком большим (субдискретизация), lsim выдает предупреждение, предлагающее, чтобы вы использовали более соответствующий шаг расчета, но использовали заданный шаг расчета. См. Алгоритмы для обсуждения шагов расчета.
lsim(sys,u,t,x0) далее задает начальное условие x0 для системных состояний. Этот синтаксис применяется только когда sys модель в пространстве состояний. x0 вектор, записи которого являются начальными значениями соответствующих состояний sys.
lsim(sys,u,t,x0,method) явным образом задает, как входные значения должны быть интерполированы между выборками, когда sys система непрерывного времени. Задайте method как одно из следующих значений:
'zoh' — Нулевой порядок использования содержит
'foh' — Используйте линейную интерполяцию (хранение первого порядка)
Если вы не задаете метод, lsim выбирает метод интерполяции автоматически на основе гладкости u сигнала.
lsim(sys1,...,sysn,u,t) симулирует ответы нескольких моделей динамической системы к той же входной истории tU и графики эти ответы на одной фигуре. Можно также использовать x0 и method входные параметры при вычислении ответов многоуровневых моделей.
lsim(sys1,LineSpec1,...,sysN,LineSpecN,u,t) задает стиль линии, маркер и цвет каждого из откликов системы в графике. Можно также использовать x0 и method входные параметры с этим синтаксисом. Каждый LineSpec аргумент задан как вектор один, два, или три символа. Символы могут появиться в любом порядке. Например, следующий код строит ответ sys1 как желтая пунктирная линия и ответ sys2 как зеленая пунктирная линия:
lsim(sys1,'y:',sys2,'g--',u,t,x0)
Для получения дополнительной информации о конфигурировании этого аргумента, смотрите LineSpec входной параметр plot функция.
y = lsim(___) возвращает отклик системы y, произведенный в те же времена как вход (t). Выход y массив, имеющий столько же строк сколько выборки времени (length(t)) и столько столбцов, сколько система выходные параметры. Никакой график не построен на экране. Можно использовать этот синтаксис с любым из входных параметров, описанных в предыдущих синтаксисах кроме LineSpec аргументы.
[y,t,x] = lsim(___) также возвращает временной вектор t используемый в симуляции и траекториях состояния x (только для моделей в пространстве состояний). Выход x имеет столько же строк сколько выборки времени (length(t)) и столько же столбцов сколько системные состояния. Можно использовать этот синтаксис с любым из входных параметров, описанных в предыдущих синтаксисах кроме LineSpec аргументы.
lsim(sys) открывает Линейный графический интерфейс пользователя Инструмента Симуляции. Для получения дополнительной информации о работе с этим графический интерфейсом пользователя, смотрите Работу с Линейным Инструментом Симуляции.
Симулируйте и постройте ответ следующей системы к прямоугольной волне с периодом четырех секунд:
Создайте передаточную функцию и сгенерируйте прямоугольную волну с gensig. Произведите каждые 0,1 секунды в течение 10 секунд.
H = [tf([2 5 1],[1 2 3]);tf([1 -1],[1 1 5])];
[u,t] = gensig('square',4,10,0.1);Затем симулируйте с lsim.
lsim(H,u,t)
График отображает и прикладной сигнал и ответ.
Загрузите данные об оценке, чтобы оценить модель.
load(fullfile(matlabroot,'toolbox','ident','iddemos','data','dcmotordata')); z = iddata(y,u,0.1,'Name','DC-motor');
z iddata объект, который хранит данные об оценке с 2 выходами с 1 входом с шагом расчета 0,1 секунды.
Оцените модель в пространстве состояний порядка 4 с помощью данных об оценке z.
[sys,x0] = n4sid(z,4);
sys предполагаемая модель и x0 предполагаемые начальные состояния.
Симулируйте ответ sys использование тех же входных данных как тот, используемый в оценке и начальных состояниях, возвращенных командой оценки.
[y,t,x] = lsim(sys,z.InputData,[],x0);
Здесь, y отклик системы, t временной вектор, используемый в симуляции и x траектория состояния.
Сравните симулированный ответ y к измеренному ответу z.OutputData для обоих выходных параметров.
subplot(211), plot(t,z.OutputData(:,1),'k',t,y(:,1),'r') legend('Measured','Simulated') subplot(212), plot(t,z.OutputData(:,2),'k',t,y(:,2),'r') legend('Measured','Simulated')
Системы дискретного времени симулированы с ltitr (пространство состояний) или filter (передаточная функция и нули, полюса и усиление).
Системы непрерывного времени дискретизируются с c2d использование любого 'zoh' или 'foh' метод ('foh' используется в сглаженных входных сигналах и 'zoh' для прерывистых сигналов, таких как импульсы или прямоугольные волны). Шаг расчета установлен в интервал dt между предоставленными пользователями выборками времени t.
Выбор шага расчета может решительно влиять на результаты симуляции. Чтобы проиллюстрировать почему, рассмотрите модель второго порядка
Чтобы симулировать его ответ на прямоугольную волну с периодом 1 секунда, можно продолжить можно следующим образом:
w2 = 62.83^2; h = tf(w2,[1 2 w2]); t = 0:0.1:5; % vector of time samples u = (rem(t,1) >= 0.5); % square wave values lsim(h,u,t)
lsim оценивает заданный шаг расчета и выдает предупреждение:
Warning: Input signal is undersampled. Sample every 0.016 sec or faster.
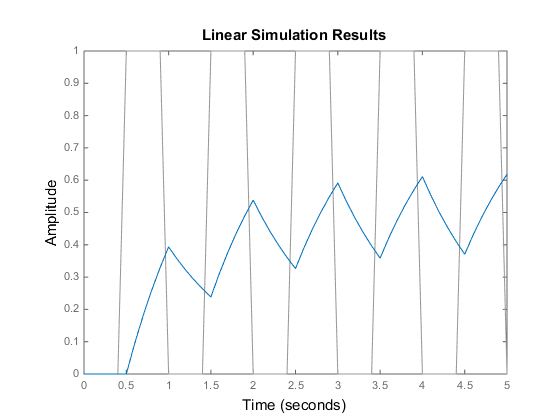
Чтобы изменить к лучшему этот ответ, дискретизируйте H (s) с помощью рекомендуемого шага расчета:
dt = 0.016; ts = 0:dt:5; us = (rem(ts,1) >= 0.5); hd = c2d(h,dt); lsim(hd,us,ts)
Этот ответ предоставляет сильное колебательное поведение, которое скрыто в субдискретизируемой версии.