tpaps

Сплайн сглаживания тонкой пластины

Синтаксис

tpaps(x,y) tpaps(x,y,p) [...,p] = tpaps(...)

Описание

tpaps(x,y) stform тонкой пластины, сглаживающей сплайн f для сайтов определенных данных x(:,j) и значения определенных данных y(:,j). x(:,j) должны быть отличные точки в плоскости, значения могут быть скалярами, векторами, матрицами, даже массивы ND, и должно быть точно столько же значений, сколько существуют сайты.

Тонкая пластина, сглаживающая сплайн f, является уникальным минимизатором взвешенной суммы

$p E (f) + (1 - p) R (f)$

с E (f) ошибочная мера

$E (f) = \sum_{j} {| y (:, j) - f (x (:, j)) |}^{2}$

и R (f) мера по шероховатости

$R (f) = {\int (| D_{1} D_{1} f |}^{2} + 2 {| D_{1} D_{2} f |}^{2} + {| D_{2} D_{2} f |}^{2})$

Здесь, интеграл взят по всему R ², |z|2 обозначает сумму квадратов всех записей z, и _Dif обозначает частную производную f относительно ее i th аргумент, следовательно подынтегральное выражение включает вторые частные производные f. Параметр сглаживания p выбран так, чтобы (1-p)/p равняется среднему значению диагональных элементов матричного A, с A + (1-p)/p*eye(n) матрица коэффициентов линейной системы для n коэффициенты сглаживания шлицуют, чтобы быть определенными. Этот выбор p предназначается, чтобы гарантировать, что мы являемся промежуточными эти два экстремальных значения интерполяции (когда p близко к 1 и матрицей коэффициентов является по существу A) и полное сглаживание (когда p близко к 0 и матрица коэффициентов является по существу кратным единичной матрице). Это должно служить хорошим первым предположением для p.

tpaps(x,y,p) также вводит параметр сглаживания, p, номер между 0 и 1. Когда параметр сглаживания варьируется от 0 до 1, сплайн сглаживания варьируется от приближения наименьших квадратов до данных линейным полиномом когда p 0, к тонкой пластине шлицуют interpolant к данным когда p 1.

[...,p] = tpaps(...) также возвращает параметр сглаживания, на самом деле используемый.

Примеры

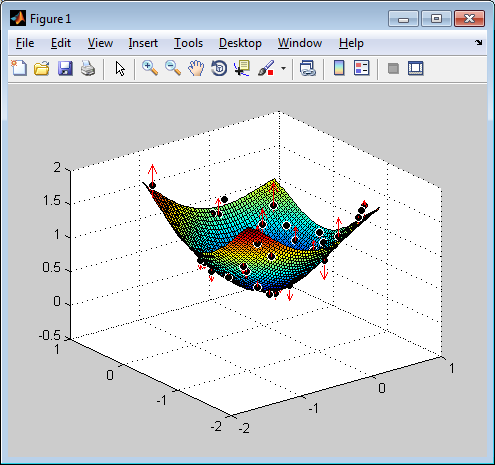
Пример 1. Следующий код получает значения сглаженной функции на 31 случайным образом выбранном сайте, добавляет некоторый случайный шум к этим значениям, и затем использует tpaps восстановить базовые точные сглаженные значения. Проиллюстрировать как хорошо tpaps делает в этом случае, графики кода, в дополнение к сплайну сглаживания, точные значения (как черные шары), а также каждое продвижение стрелы от сглаживавшего значения до соответствующего шумного значения.

rng(23); nxy = 31;
xy = 2*(rand(2,nxy)-.5); vals = sum(xy.^2);
noisyvals = vals + (rand(size(vals))-.5)/5;
st = tpaps(xy,noisyvals); fnplt(st), hold on
avals = fnval(st,xy);
plot3(xy(1,:),xy(2,:),vals,'wo','markerfacecolor','k')
quiver3(xy(1,:),xy(2,:),avals,zeros(1,nxy),zeros(1,nxy), ...
         noisyvals-avals,'r'), hold off

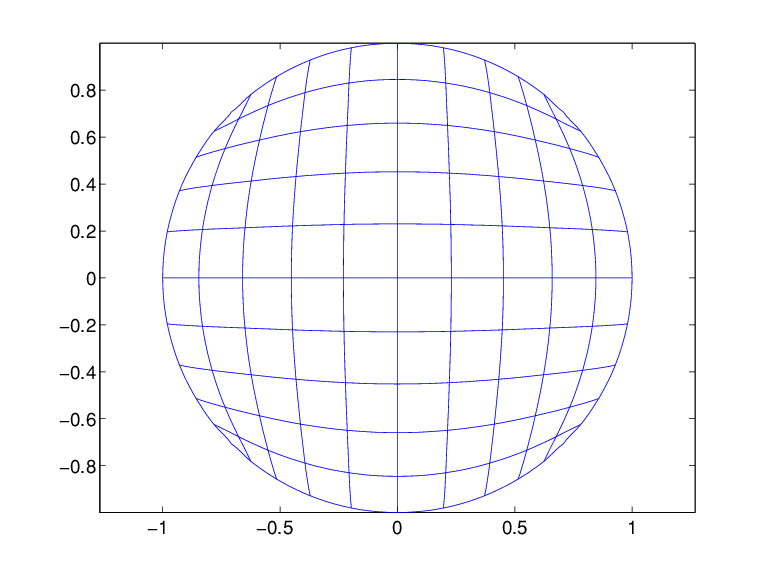
Пример 2. Следующий код использует сплайн тонкой пластины интерполяции для значений данных с векторным знаком, чтобы создать карту от плоскости до плоскости, которая несет модульный квадрат {x: |x (j) | ≤ 1, j = 1:2} приблизительно на единичный диск {x: x (1) ² + x (2) ² ≤ 1}, как показано изображением сгенерированы.

n = 64; t = linspace(0,2*pi,n+1); t(end) = [];
values = [cos(t); sin(t)];
centers = values./repmat(max(abs(values)),2,1);
st = tpaps(centers, values, 1);
fnplt(st), axis equal

Отметьте выбор 1 для параметра сглаживания здесь, чтобы получить интерполяцию.

Ограничения

Определение сплайна сглаживания включает решение линейной системы со столькими же неизвестных, сколько существуют точки данных. Поскольку матрица этой линейной системы полна, решение может занять много времени, даже если, как имеет место здесь, итеративная схема используется, когда существует больше чем 728 точек данных. Быстрота сходимости той итерации строго под влиянием p, и медленнее больший p . Так, для больших проблем используйте интерполяцию, т.е. p равняйтесь 1, только если можно выкроить время.

Смотрите также

csaps | spaps

Документация