Удалите низкочастотный шум в Simulink Используя нормированный адаптивный фильтр LMS

Адаптивные фильтры отслеживают динамический характер системы и позволяют вам устранять изменяющиеся во времени сигналы. Библиотеки DSP System Toolbox™ содержат блоки, которые реализуют least-mean-square (LMS), блок LMS, быстрый блок LMS и рекурсивные наименьшие квадраты (RLS) адаптивные алгоритмы фильтра. Эти фильтры минимизируют различие между выходным сигналом и желаемым сигналом путем изменения их коэффициентов фильтра. В зависимости от времени выходной сигнал адаптивного фильтра более тесно аппроксимирует сигнал, который вы хотите воспроизвести.

Спроектируйте адаптивный фильтр в Simulink

В этом примере вы проектируете адаптивный фильтр LMS, чтобы удалить низкочастотный шум в вашем сигнале:

  1. Если модель, в которой вы создали, Добавляет, что Цифровой фильтр к Вашей Модели не открыт на вашем рабочем столе, можно открыть эквивалентную модель путем ввода

    ex_gstut5

    в командной строке MATLAB®.

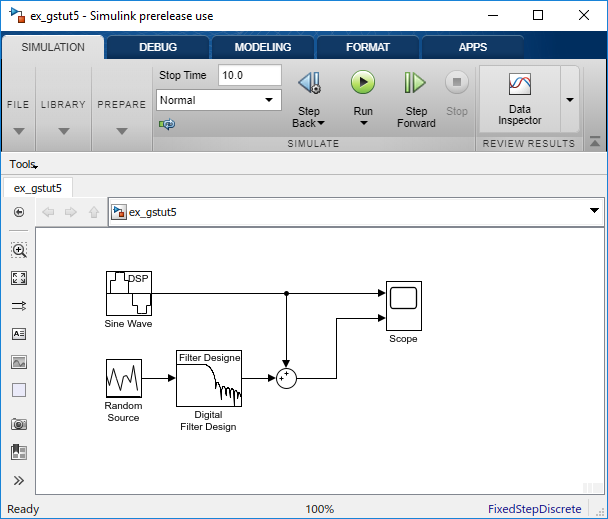
  2. Откройте библиотеку DSP System Toolbox путем ввода dsplib в командной строке MATLAB.

  3. Удалите низкочастотный шум из своего сигнала путем добавления блока LMS Filter в систему. В сценарии самолета это эквивалентно вычитанию шума ветра в кабине с входа на микрофон. Дважды кликните библиотеку Filtering, и затем дважды кликните библиотеку Adaptive Filters. Добавьте блок LMS Filter в свою модель.

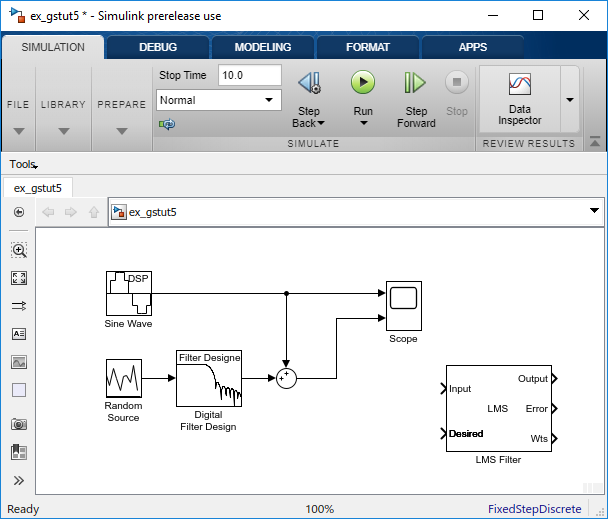
  4. Установите параметры блоков LMS Filter моделировать выход блока Digital Filter Design. Откройте диалоговое окно LMS Filter путем двойного клика по блоку. Установите и примените параметры блоков можно следующим образом:

    • Algorithm = Normalized LMS

    • Filter length = 32

    • Specify step size via = Dialog

    • Step size (mu) = 0.1

    • Leakage factor (0 to 1) = 1.0

    • Initial value of filter weights = 0

    • Снимите флажок Adapt port.

    • Reset port = None

    • Установите флажок Output filter weights.

На основе этих параметров блок LMS Filter вычисляет веса фильтра с помощью нормированных уравнений LMS. Порядок фильтра, которого вы задали, совпадает с порядком фильтра блока Digital Filter Design. Параметр Step size (mu) задает гранулярность шагов обновления фильтра. Поскольку вы устанавливаете параметр Leakage factor (0 to 1) на 1.0, текущие содействующие значения фильтра зависят от начальных условий фильтра и всех предыдущих входных значений. Начальное значение весов фильтра (коэффициенты) является нулем. Поскольку вы установили флажок Output filter weights, порт Wts появляется на блоке. Блок выводит веса фильтра от этого порта.

Теперь, когда вы установили параметры блоков блока LMS Filter, можно включить этот блок в блок-схему.

Добавьте адаптивный фильтр в свою модель

В этом примере вы восстанавливаете свой исходный синусоидальный сигнал путем слияния адаптивного фильтра, вы спроектировали в Проекте Адаптивный Фильтр в Simulink в вашу систему. В сценарии самолета адаптивный фильтр моделирует низкочастотный шум, который услышали в кабине. В результате можно удалить шум так, чтобы речь пилота была единственным входом к микрофону:

  1. Если модель, вы создали в Проекте Адаптивный Фильтр в Simulink, не открыта на вашем рабочем столе, можно открыть эквивалентную модель путем ввода

    ex_gstut6

    в командной строке MATLAB.

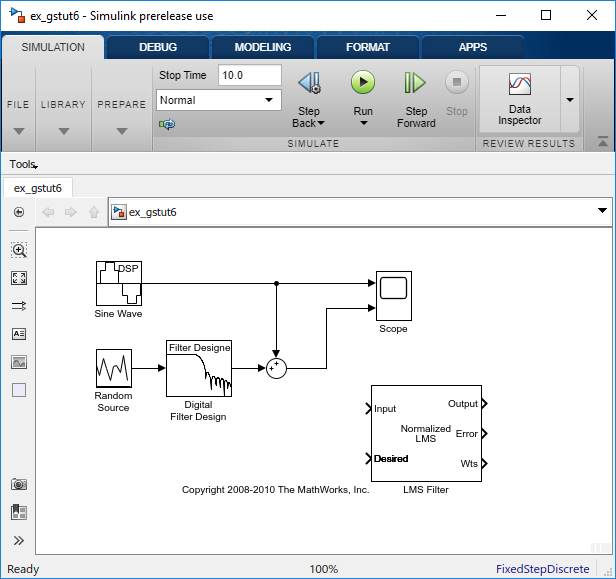
  2. Добавьте блок Sum в свою модель, чтобы вычесть выход адаптивного фильтра от синусоидального сигнала с низкочастотным шумом. От библиотеки Simulink® Math Operations перетащите блок Sum в свою модель. Откройте диалоговое окно Sum путем двойного клика по этому блоку. Измените параметр List of signs в | + - и затем нажмите OK.

  3. Включите блок LMS Filter в свою систему.

    1. Соедините выход Случайного Исходного блока к Input port блока LMS Filter. В сценарии самолета случайный шум является белым шумом, измеренным датчиком за пределами самолета. Блок LMS Filter моделирует эффект фюзеляжа самолета на шуме.

    2. Соедините выход блока Digital Filter Design к Требуемому порту на блоке LMS Filter. Это - сигнал, который вы хотите, чтобы блок LMS воспроизвел.

    3. Соедините выход блока LMS Filter к отрицательному порту блока Sum, который вы добавили на шаге 2.

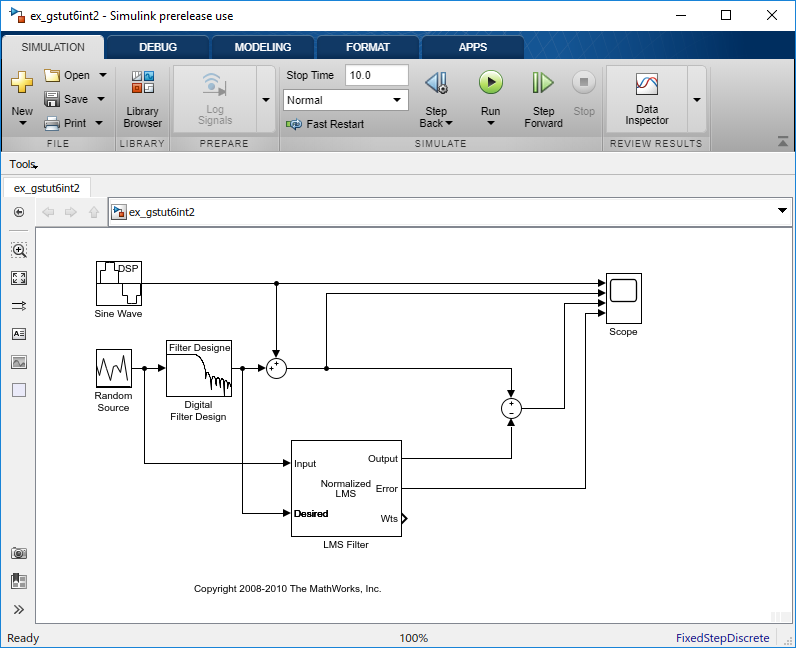
    4. Соедините выход первого блока Sum к положительному порту второго блока Sum. Ваша модель должна теперь выглядеть похожей на следующую фигуру.

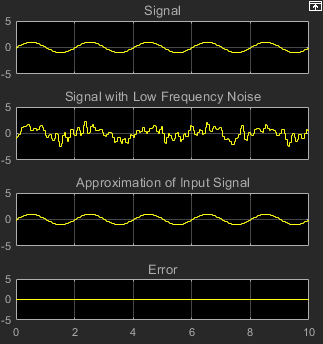
    Положительный вход со вторым блоком Sum является суммой входного сигнала и низкочастотного шума, s (n) + y. Отрицательный вход со вторым блоком Sum является лучшей оценкой блока LMS Filter низкочастотного шума, y'. Когда вы вычитаете два сигнала, вас оставляют с приближением входного сигнала.

    s(n)\approx=s(n)+y−y'

    В этом уравнении:

    • s (n) является входным сигналом

    • s(n)\approx приближение входного сигнала

    • y является шумом, созданным блоком Random Source и блоком Digital Filter Design

    • y' является приближением блока LMS Filter шума

    Поскольку блок LMS Filter может только аппроксимировать шум, существует все еще различие между входным сигналом и приближением входного сигнала. На последующих шагах вы настраиваете блок Scope, таким образом, можно сравнить исходный синусоидальный сигнал с его приближением.

  4. Добавьте два дополнительных входных параметров и оси с блоком Scope. Откройте диалоговое окно Scope путем двойного клика по блоку Scope. Нажмите кнопку Parameters. Для параметра Number of axes введите 4. Закройте диалоговое окно путем нажатия на OK.

  5. Подпишите новые оси Осциллографа. В окне Scope щелкните правой кнопкой по третьим осям и выберите Axes properties. Свойства Scope: ось 3 диалоговых окна открывается. В поле Title введите Approximation of Input Signal. Закройте диалоговое окно путем нажатия на OK. Повторите эту процедуру для четвертых осей и пометьте ее Error.

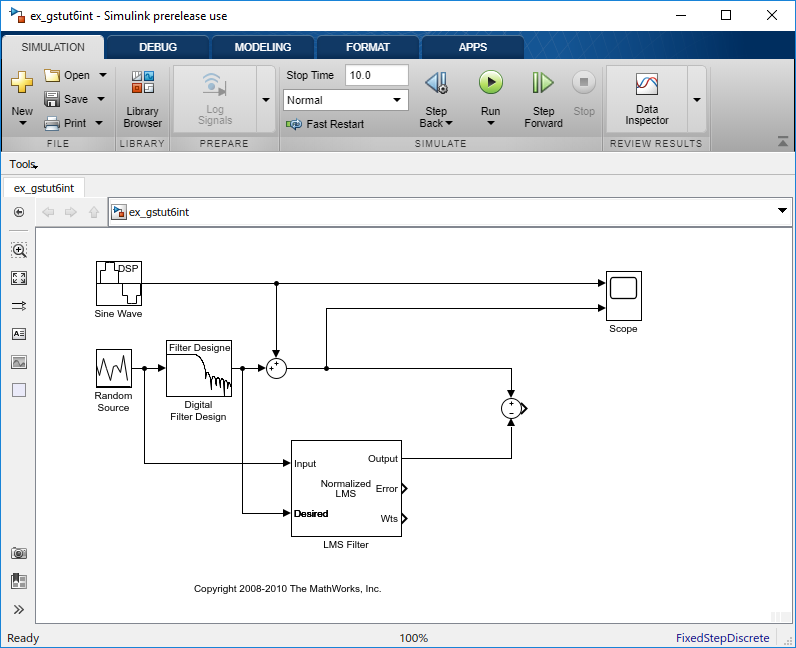
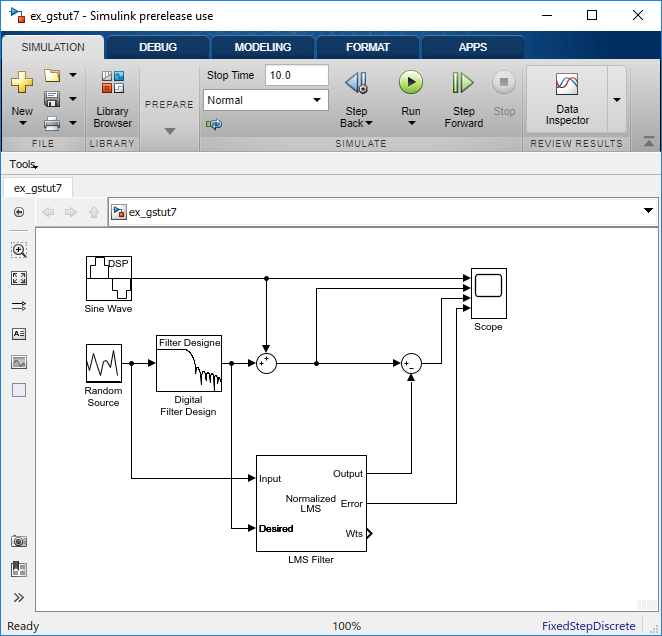
  6. Соедините выход второго блока Sum к третьему порту блока Scope.

  7. Соедините выход порта Error на блоке LMS Filter к четвертому порту блока Scope. Ваша модель должна теперь выглядеть похожей на следующую фигуру.

В этом примере выход порта Error является различием между желаемым сигналом фильтра LMS и его выходным сигналом. Поскольку ошибка никогда не является нулем, фильтр продолжает изменять коэффициенты фильтра для того, чтобы лучше аппроксимировать низкочастотный шум. Чем лучше приближение, тем больше низкочастотного шума, который может быть удален из синусоидального сигнала. В следующей теме, Просматривают Коэффициенты Вашего Адаптивного Фильтра, вы изучаете, как просмотреть коэффициенты вашего адаптивного фильтра, когда они изменяются со временем.

Просмотрите коэффициенты своего адаптивного фильтра

Коэффициенты адаптивного фильтра изменяются со временем в соответствии с выбранным алгоритмом. Если алгоритм оптимизирует производительность фильтра, эти коэффициенты фильтра достигают своих установившихся значений. Можно просмотреть изменение коэффициентов, в то время как симуляция запускается, чтобы видеть, что они обосновываются к их установившимся значениям. Затем можно определить, можно ли реализовать эти значения в фактической системе:

  1. Если модель, в которой вы создали, Добавляет, что Адаптивный Фильтр к Вашей Модели не открыт на вашем рабочем столе, можно открыть эквивалентную модель путем ввода

    ex_gstut7

    в командной строке MATLAB. Обратите внимание на то, что порт Wts адаптивного фильтра, который выводит веса фильтра, все еще должен быть соединен.

  2. Откройте библиотеку DSP System Toolbox путем ввода dsplib в командной строке MATLAB.

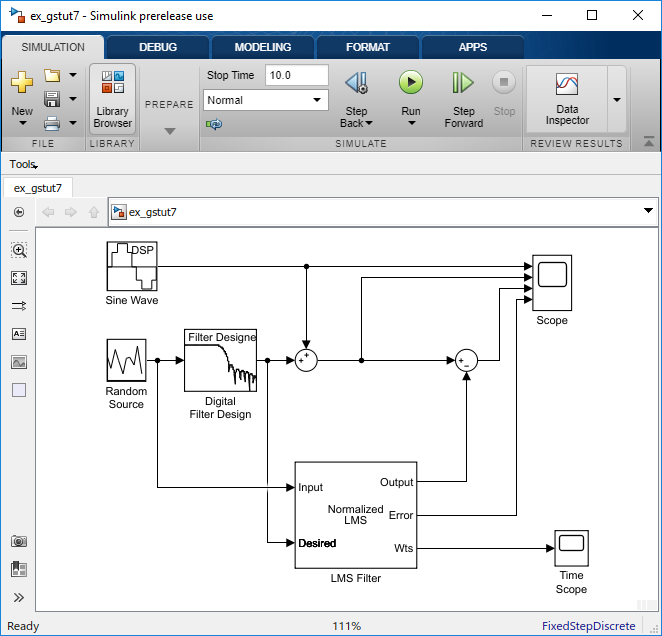
  3. Просмотрите коэффициенты фильтра путем соединения блока Time Scope с портом Wts блока LMS Filter.

  4. На блоке Time Scope измените следующие свойства настройки:

    • Time span = 0.05

    • Y-limits (Minimum) = -0.15

    • Y-limits (Maximum) = 0.5

  5. Открытые Настройки Модели. Во вкладке Modeling нажмите Model Settings. В панели Solver, набор эти параметры конфигурации:

    1. Stop time = inf

    2. Type = Fixed-step

    3. Solver = discrete (no continuous states)

    Мы рекомендуем эти параметры конфигурации для моделей, которые содержат блоки DSP System Toolbox. Поскольку эти блоки вычисляют значения непосредственно вместо того, чтобы решить дифференциальные уравнения, необходимо сконфигурировать Решатель Simulink, чтобы вести себя как планировщик. Решатель, в то время как в режиме планировщика, использует шаг расчета блока, чтобы определить, когда код позади каждого блока выполнен. Например, шагом расчета Sine wave и Случайных Исходных блоков в этой модели является 0.05. Решатель выполняет код позади этих блоков и любого блока с этим шагом расчета, один раз в 0,05 секунды.

    Примечание

    При работе с моделями, которые содержат блоки DSP System Toolbox, используйте исходные блоки, которые позволяют вам задать их шаг расчета. Если ваш исходный блок не имеет параметра Sample time, необходимо добавить блок Zero-Order Hold в модели и использовать ее, чтобы задать шаг расчета. Для получения дополнительной информации смотрите Исходные блоки Непрерывного времени. Исключением к этому правилу является блок Constant, который может иметь постоянный шаг расчета. Когда это делает, Simulink выполняет этот блок и записывает постоянное значение однажды в начале симуляции и любое время, вы настраиваете параметр. Это допускает более быстрые симуляции и более компактный сгенерированный код.

  6. Запустите свою модель и просмотрите поведение ваших коэффициентов фильтра в Осциллографе Времени, который открывается автоматически, когда ваша симуляция запускается. В зависимости от времени коэффициенты фильтра приближаются к своим установившимся значениям.

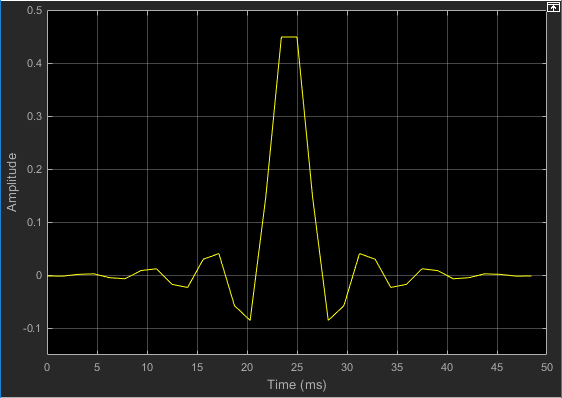
    Можно также просмотреть поведение системы в окне Scope. В зависимости от времени вы видите, что ошибка уменьшиться и приближение входного сигнала более тесно совпадает с исходным синусоидальным входным сигналом.

Вы теперь создали модель, способную к адаптивному подавлению помех.

Сводные данные

Вы изучили, как спроектировать фильтр lowpass с помощью блока Digital Filter Design. Вы также изучили, как создать адаптивный фильтр с помощью блока LMS Filter. Продукт DSP System Toolbox имеет другие блоки, способные к разработке и реализации цифровых и адаптивных фильтров. Для получения дополнительной информации о возможностях фильтрации этого продукта смотрите Анализ Создания фильтра и Фильтра.

Поскольку все блоки в этой модели имеют тот же шаг расчета, эта модель является одним уровнем, и Simulink запустил его в SingleTasking режим решателя. Если блоки в вашей модели имеют различные шаги расчета, ваша модель является многоскоростной, и Simulink может запустить его в MultiTasking режим решателя. Для получения дополнительной информации о режимах решателя смотрите Рекомендуемые Настройки для Симуляций Дискретного времени.

Чтобы изучить, как сгенерировать код из вашей модели с помощью продукта Simulink Coder™, смотрите, Генерируют код С из Модели Simulink.

Смотрите также

|

Похожие темы

Документация DSP System Toolbox
Поддержка
Для просмотра документации необходимо авторизоваться на сайте