БПФ с высоким разрешением фрагмента спектра
dsp.ZoomFFT Система object™ вычисляет быстрое преобразование Фурье (FFT) сигнала по фрагменту частот в интервале Найквиста. Путем устанавливания соответствующий коэффициент децимации D и выборки уровня Fs, можно выбрать пропускную способность частот, чтобы анализировать BW, где BW = Fs/D. Можно также выбрать определенную область значений частот, чтобы анализировать в интервале Найквиста путем выбора центральной частоты желаемой полосы.
Разрешение сигнала является отношением Fs и длины БПФ (L). Используя БПФ изменения масштаба, можно сохранить то же разрешение, которого вы достигли бы с полноразмерным БПФ на вашем исходном сигнале путем вычисления маленького БПФ на более коротком сигнале. Более короткий сигнал прибывает из десятикратного уменьшения исходного сигнала. Сбережения прибывают из способности вычислить намного более короткий БПФ при достижении того же разрешения. Для фактора децимации D новым уровнем выборки, Fsd, является Fs/D, и новым форматом кадра (и длина БПФ) является Ld = L/D. Разрешением подкошенного сигнала является Fsd/Ld = Fs/L. Чтобы достигнуть более высокого разрешения более короткой полосы, используйте исходную длину БПФ, L, вместо подкошенной длины БПФ, Ld.
Вычислить БПФ фрагмента спектра:
Создайте dsp.ZoomFFT объект и набор его свойства.
Вызовите объект с аргументами, как будто это была функция.
Чтобы узнать больше, как Системные объекты работают, смотрите то, Что Системные объекты? MATLAB.
zfft = dsp.ZoomFFTzfft, это выполняет БПФ на фрагменте частотного диапазона входного сигнала. Объект определяет частотный диапазон, по которому можно выполнить БПФ с помощью заданной центральной частоты и значений фактора децимации.
zfft = dsp.ZoomFFT(d)d.
zfft = dsp.ZoomFFT(d,Fc)d, и набор свойств CenterFrequency к Fc.
zfft = dsp.ZoomFFT(d,Fc,Fs)d, набор свойств CenterFrequency к Fc, и набор свойств SampleRate к Fs.
zfft = dsp.ZoomFFT(Name,Value)
zfft = dsp.ZoomFFT(2,2e3,48e3,'FFTLength',64);Чтобы использовать объектную функцию, задайте Системный объект как первый входной параметр. Например, чтобы выпустить системные ресурсы Системного объекта под названием obj, используйте этот синтаксис:
release(obj)
Вычислите БПФ поддиапазона [на 1 500 Гц 2 500 Гц] с помощью БПФ изменения масштаба в сигнале, произведенном на уровне 48 кГц.
Инициализация
Установите центральную частоту на 2 кГц и пропускную способность интереса для 1 кГц. Пропускная способность сосредоточена на центральной частоте. Фактором децимации является отношение входной частоты дискретизации, 48 кГц и пропускной способности интереса, 1 кГц. Выберите длину FFT 64. Установите размер входного кадра быть временами фактора децимации длина БПФ. Создайте dsp.ZoomFFT объект с заданным фактором децимации, сосредоточьте частоту, частоту дискретизации и длину БПФ.
Fs = 48e3;
CF = 2e3;
BW = 1e3;
D = Fs/BW;
fftlen = 64;
L = D * fftlen;
zfft = dsp.ZoomFFT(D,CF,Fs,'FFTLength',fftlen);
Частоты
БПФ вычислен по частотам, запускающимся на уровне 1 500 Гц, и расположен с интервалами $Fs / (D*fftLen) $Hz независимо, который является разрешением или минимальной частотой, которая может быть различена. Количество частот, на которых вычисляется БПФ изменения масштаба, равняется длине БПФ.
Fsd = Fs/D; F = CF + (Fsd/fftlen)*(0:fftlen-1)-Fsd/2;
Инициализируйте осциллограф
Создайте график массивов показать частоты в F.
ap = dsp.ArrayPlot('XDataMode','Custom','CustomXData',F,... 'YLabel','z .* conj(z)','XLabel','Frequency (Hz)','YLimits',[0 1.1e3],... 'Title',sprintf('Decimation Factor = %d. Center Frequency = %d Hz. Resolution = %f Hz',D, CF,(Fs/D)/fftlen));
Генератор Sine wave
Создайте синусоиду с частотами на уровне 1 625 Гц, 2 000 Гц и 2 125 Гц.
tones = [1625 2000 2125]; sine = dsp.SineWave('SampleRate',Fs,'Frequency',tones,'SamplesPerFrame',L);
Потоковая передача
Передайте шумную синусоиду с частотой дискретизации 48 кГц. Вычислите БПФ изменения масштаба этой синусоиды в поддиапазоне [1 500 Гц 2 500 Гц]. Перестройте преобразование Фурье путем сдвига нулевой частотной составляющей к центру массива. Просмотрите тоны на уровне 1 625 Гц, 2 000 Гц и 2 125 Гц в графике массивов.
for i = 1:1000 x = sum(sine(),2)+1e-1*randn(L,1); z = zfft(x); z = fftshift(z); ap(z.*conj(z)); end
dsp.ZoomFFT объект принимает входные параметры переменного размера, пока вход является кратным фактору децимации. Количество входных каналов не может измениться.
Создайте dsp.ZoomFFT объект с фактором децимации 4, сосредоточьте частоту 2 кГц и входную частоту дискретизации 48 кГц. Передайте случайный вход с 4*64 строками и 2 столбцами. Варьируйтесь количество строк к 4*128 и 4*32. Получившиеся длины БПФ равняются 64, 128, и 32, соответственно. Размер выходных параметров [64 2], [128 2], и [32 2], соответственно.
zfft = dsp.ZoomFFT(4,2e3,48e3); y1 = zfft(randn(4*64,2)); y2 = zfft(randn(4*128,2)); y3 = zfft(randn(4*32,2));
Установите длину БПФ как 256 и передайте входные параметры переменного размера. Размер всех выходных параметров [256 2].
release(zfft); zfft.FFTLength = 256; y4 = zfft(randn(4*64,2)); y5 = zfft(randn(4*128,2)); y6 = zfft(randn(4*32,2));
Алгоритм бпф изменения масштаба усиливает полосу пропускания, фильтрующую прежде, чем вычислить БПФ сигнала. Концепция полосовой фильтрации, это предполагает, что вы интересуетесь полосой [F1, F2] исходного входного сигнала, произведенного на уровне Гц Fs. Если вы передаете этот сигнал через комплексный (односторонний) полосовой фильтр, сосредоточенный в Fc = (F1 +F2)/2, с пропускной способностью BW = F2 – F1, и затем прореживаете сигнал фактором D = пол (Fs/BW), желаемая полоса сводится к основной полосе.
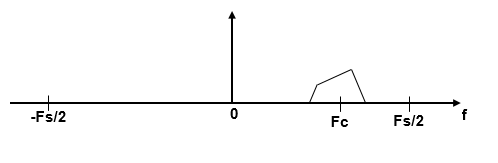
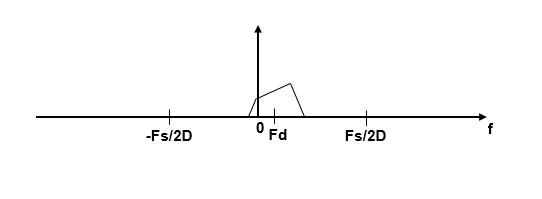
Если Fc нельзя выразить в форме k ×Fs/D, где k является целым числом, то переключенный, подкошенный спектр не сосредоточен в DC. В этом случае центральная частота переводится в Fd.
Комплексный полосовой фильтр получен первой разработкой прототипа фильтра lowpass и затем умножением коэффициентов lowpass с комплексной экпонентой. Этот алгоритм использует многоскоростной, многоступенчатый КИХ-фильтр в качестве прототипа фильтра lowpass. Чтобы получить полосовой фильтр, коэффициенты каждого этапа являются переключенной частотой. Фактором децимации является совокупный фактор децимации каждого этапа. Комплексный полосовой фильтр, сопровождаемый decimator, реализован с помощью эффективной многофазной структуры. Для получения дополнительной информации о проекте комплексного полосового фильтра от многоскоростного многоступенчатого КИХ-прототипа фильтра смотрите БПФ Изменения масштаба и Комплексный Проект Полосового фильтра.
[1] Харрис, Обработка сигналов Ф.Дж. Малтирэйта для Систем связи. Prentice Hall, 2004, стр 208–209.